
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Главные напряжения, главные площадки
На наклонной площадке, у которой орт нормали
Надо найти Очевидно, что
Из этого следует, что
Раскрывая этот определитель, получим, с учетом закона парности касательных напряжений:
После перемножений и приведения подобных членов найдем
Где:
Величины Решение кубического уравнения (11.5) дает три корня для Инварианты напряженного состояния через главные напряжения определяются с учетом (11.6) так:
Здесь учтено, что на главных площадках нет касательных напряжений.
Экстремальные касательные напряжения
Вырежем из тела малый тетраэдр, у которого координатные оси совпадают с направлениями главных напряжений, т.е. на невидимых площадках действуют только Полное напряжение на ней
Касательные напряжения на наклонной площадке найдем по (11.4), подстановкой (9):
После преобразований получим
Условие экстремальности
Окончательно
Аналогично, на площадках с решениями 1) и 2) можно найти экстремальные Итак, имеем три площадки, на которых действуют экстремальные касательные напряжения:
|
|||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 147; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.75.227 (0.006 с.) |
 совпадает с направлением
совпадает с направлением  , величина
, величина  , а
, а  будет экстремально и равно
будет экстремально и равно  ). А напряжения на ней обозначим
). А напряжения на ней обозначим  . Все его проекции на оси
. Все его проекции на оси  будут
будут 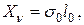
 . Подставим их в формулы (11.1):
. Подставим их в формулы (11.1): или
или  (4)
(4) и
и 
 .
. . (5)
. (5)
 . (6)
. (6) (7)
(7) (8)
(8) . (11.5)
. (11.5)
 . (11.6)
. (11.6) и
и  называются инвариантами тензора напряжений
называются инвариантами тензора напряжений  (легко убедится, что
(легко убедится, что  , которые и называются главными напряжениями. Итак, имеем три главных напряжения, которые действуют на трех главных площадках, определяемых
, которые и называются главными напряжениями. Итак, имеем три главных напряжения, которые действуют на трех главных площадках, определяемых  . Например, найдем
. Например, найдем  главной площадки, где действует
главной площадки, где действует  . Для этого составим три уравнения:
. Для этого составим три уравнения:  и любые два уравнения из системы (4), подставляя в них
и любые два уравнения из системы (4), подставляя в них  . Решая эти три уравнения, найдем
. Решая эти три уравнения, найдем  и
и  . Можно показать, что главные площадки взаимно ортогональны.
. Можно показать, что главные площадки взаимно ортогональны.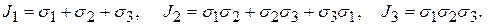
 и
и  на наклонной площадке с ортом
на наклонной площадке с ортом  ,
, 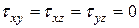 , т.к. на главных площадках касательных напряжений нет:
, т.к. на главных площадках касательных напряжений нет: (9)
(9) .
. (10)
(10) и
и  дает три решения, которые определяют три площадки с экстремальными
дает три решения, которые определяют три площадки с экстремальными  Третьему решению соот-ветствуют рис.11.2, т.е. это площадка под углами 45° к осям с
Третьему решению соот-ветствуют рис.11.2, т.е. это площадка под углами 45° к осям с  и
и  в выражение (10), получим
в выражение (10), получим
 Рис.11.2
Рис.11.2
 .
. . (11)
. (11) и
и  .
. . (11.7)
. (11.7)


