
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ напряженно-деформированногоСтр 1 из 3Следующая ⇒
Анализ напряженно-деформированного Состояния в точке тела
Часть I. Объемное напряженное состояние
Напряжения на наклонных площадках (Условия на поверхности)
определим так:
На этих невидимых, отрицательных площадках, действуют положительные напряжения, определяемые
Объемные силы
Составляя уравнения статики
Если площадка
Полное, нормальное и касательное напряжения на Наклонной площадке
На рис. 11.1 показаны компоненты полного напряжения
Подставляя сюда формулы (11.1), найдем
Полное напряжение
Касательное напряжение
Октаэдрические нормальные и касательные Напряжения Площадки, равнонаклоненные к направлениям главных напряжений, называются октаэдрическими, направляющие косинусы их
Нормальное напряжение
следовательно, Наклонных площадках
1) на составляющие по осям 2) на нормальное Очевидно: Как и в объемном напряженном состоянии, положение площадки
Напряжения
Здесь Уравнения (11.9) легко получить из условий равновесия треугольного элемента, показанного на рис.11.4 Определим площадки элемента:
Умножая напряжения на площадки, составим уравнения статики:
Подставляя (15) и сокращая на
Подставляем (11.9), получим, учитывая, что
Подставляя (14) и учитывая, что
Касательное напряжение
Подставим (14) и, учитывая, что
анализ напряженно-деформированного Состояния в точке тела
|
|||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.106.69 (0.011 с.) |
 Рис.11.1
Рис.11.1
 с тремя плоскостями, совпадающими с координатными (см. рис. 11.1). Положение в пространстве наклонной пло-щадки
с тремя плоскостями, совпадающими с координатными (см. рис. 11.1). Положение в пространстве наклонной пло-щадки 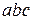 определяется нор-малью
определяется нор-малью  , направляющие конусы которой обозначим так:
, направляющие конусы которой обозначим так:
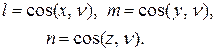 Площадку
Площадку  . Невидимые треугольные пло-щадки, перпендикулярные осям
. Невидимые треугольные пло-щадки, перпендикулярные осям  и
и  , обозначим и
, обозначим и
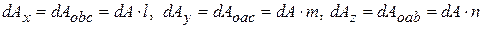 . (1)
. (1) . На наклонной площадке
. На наклонной площадке 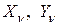 и
и  . Под действием всех напряжений, показанных на рис.11.1, тетраэдр находится в равновесии. Умножая напряжения на площадки, составим уравнение статики
. Под действием всех напряжений, показанных на рис.11.1, тетраэдр находится в равновесии. Умножая напряжения на площадки, составим уравнение статики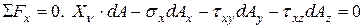 . (2)
. (2)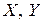 и
и  здесь не учитываются, т.к. они пропорциональны объему, который имеет третий порядок малости, а все слагаемые в (2) – второй порядок малости. Подставляя (1) в (2) и сокращая на
здесь не учитываются, т.к. они пропорциональны объему, который имеет третий порядок малости, а все слагаемые в (2) – второй порядок малости. Подставляя (1) в (2) и сокращая на 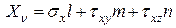 . (3)
. (3) и
и 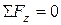 , получим еще два уравнения, которые легко записать, используя кольцевую перестановку
, получим еще два уравнения, которые легко записать, используя кольцевую перестановку  и
и 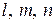 , получим три уравнения равновесия тетраэдра:
, получим три уравнения равновесия тетраэдра: (11.1)
(11.1) на наклонной площадке
на наклонной площадке 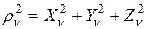 .
.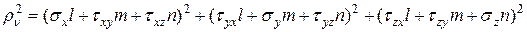 . (11.2)
. (11.2) нормальное и
нормальное и  касательное напряжения на наклонной площадке. Очевидно, что
касательное напряжения на наклонной площадке. Очевидно, что  . Напряжение
. Напряжение  можно найти, проектируя
можно найти, проектируя  . С учетом формул (11.1) получим
. С учетом формул (11.1) получим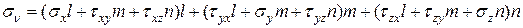 . (11.3)
. (11.3) можно найти так:
можно найти так: . (11.4)
. (11.4) , т.к. должно быть
, т.к. должно быть  .
.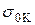 и касательное
и касательное  на этой площадке через главные напряжения найдем по формулам (9) и (10) подстановкой
на этой площадке через главные напряжения найдем по формулам (9) и (10) подстановкой 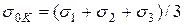 ;
; (11.8)
(11.8)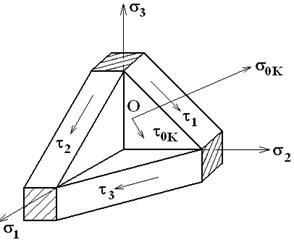 Рис.11.3
Рис.11.3
 и показаны три площадки с экстремальными касса-тельными напряжениями
и показаны три площадки с экстремальными касса-тельными напряжениями 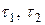 и
и  . Легко показать, что
. Легко показать, что
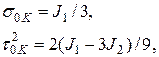
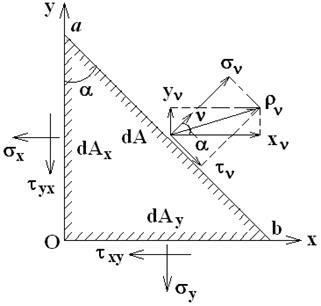 Рис. 11.4
Рис. 11.4
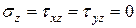 . (12)
Получим ПНС в осях
. (12)
Получим ПНС в осях 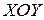 , показанное на рис. 11.4.
На наклонной площадке
, показанное на рис. 11.4.
На наклонной площадке 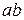 действует полное напряжение
действует полное напряжение
 и
и 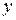 , т.е. на
, т.е. на 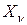 и
и 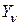 ;
; . (13)
. (13)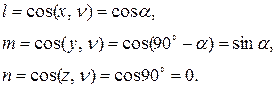 (14)
(14) :
: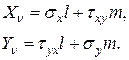 (11.9)
(11.9)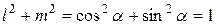 .
. . (15)
. (15)
 .
.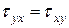 :
: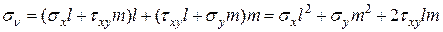 .
. , найдем
, найдем . (11.10)
. (11.10)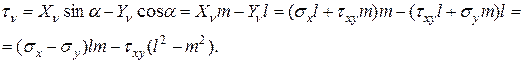
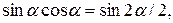

 , окончательно получим
, окончательно получим . (11.11)
. (11.11)


