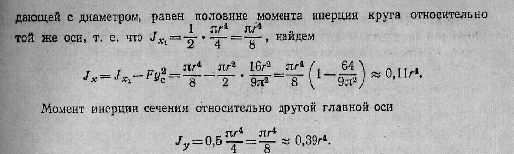Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициент Пуассона. Отнсительное изменение объемаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
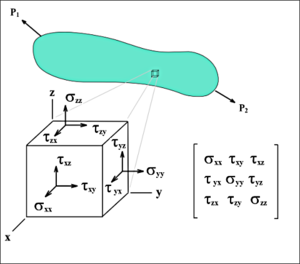
41 Те́нзор напряже́ний — тензор второго ранга, состоящий из девяти величин, представляющих механические напряжения в произвольной точке нагруженного тела. Эти девять величин записываются в виде таблицы, в которой по главной диагонали стоят нормальные напряжения в трёх взаимно перпендикулярных осях, а в остальных позициях - касательные напряжения, действующие на трёх взаимно перпендикулярных плоскостях.
Полный тензор механического напряжения элементарного объёма тела. Буквой σ обозначены нормальные механические напряжения, а касательные буквой τ. Компоненты тензора напряжений σ ij в декартовой системе координат Oxi (т.е. Oxyz) вводят следующим образом. Рассматривают бесконечно малый объем тела (сплошной среды) в виде прямоугольного параллелепипеда, грани которого ортогональны координатным осям и имеют площади dSi. На каждой грани dSi параллелепипеда действуют поверхностные силы dFi. Если обозначить проекции этих сил на оси Oxj как dFij, то компонентами тензора напряжений называют отношение проекций силы к величине площади грани, на которой действует эта сила:
По индексу i здесь суммирования нет. Компоненты σ11, σ22,σ33,обозначаемые также как σ xx, σ yy,σ zz - это нормальные напряжения, они представляют собой отношение проекции силы dFi на нормаль к рассматриваемой грани dSi:
Компоненты σ12, σ23,σ13,обозначаемые также как τ xy, τ yz,τ xz - это касательные напряжения, они представляют собой отношение проекции силы dFi на касательные направления к рассматриваемой грани dSi:
В случае линейной теории упругости тензор напряжений симметричен (так называемый закон парности касательных напряжений). Чистый сдвиг. Закон гука Чистый сдвиг — это такое напряженное состояние, когда на гранях выделенного из бруса элемента действуют только касательные напряжения. Такие грани называются площадками чистого сдвига. Величина a - абсолютный сдвиг, γ = tg γ = a/h - относительный сдвиг. По аналогии с растяжением – сжатием, закон Гука при сдвиге в абсолютных координатах имеет следующий вид:
где G - модуль сдвига или модуль упругости второго рода. Можно показать, что модуль сдвига связан с модулем упругости первого рода и коэффициентом Пуассона следующим, хорошо согласующимся с опытом, уравнением:
Для стали модуль сдвига G =8·104 МПа. Из уравнения (5.2) с учетом (5.1) может быть получен закон Гука при сдвиге в относительных координатах:
или
Закон Гука справедлив лишь до предела пропорциональности. При испытаниях на сдвиг образцов из пластичных материалов так же, как и при растяжении, наблюдается явление текучести. Предел текучести обозначается через τ т, а предел прочности – через τв.
43 Срез и смятие: общая картина деформации при смятии, условие прочности, допускаемые напряжения Деформация смятия явл. разновидностью деформации сжатия при действии силы на небольшой площади. Возникают напряжения, называющиеся напряжения смятия.1) условие прочности на смятие будет иметь вид:
Смятие материала может происходить в местах сочленения отдельных элементов конструкции. Расчет на смятие необходимо проводить как для разъемных, так и неразъемных соединений; стыковочных узлов, заклепочных соединений, сочленений тяг управления.
Величина допустимых напряжений смятия
44 Расчет заклепок на смятие и листов на разрыв. На практике целый ряд деталей и элементов конструкций работает в таких условиях, что внешние силы стремятся их разрушить именно путем сдвига. В соответствии с этим при проверке прочности таких элементов на первый план выступают касательные напряжения. Простейшими примерами подобных деталей являются болтовые и заклепочные соединения. Заклепки во многих случаях уже вытеснены сваркой; однако они имеют еще очень большое применение для соединения частей всякого рода металлических конструкций: стропил, ферм мостов, кранов, для соединения листов в котлах, судах, резервуарах и т. п. Для образования заклепочного соединения в обоих листах просверливают или продавливают отверстия. В них закладывается нагретый до красного каления стержень' заклепки с одной головкой; другой конец заклепки расклепывается ударами специального молотка или давлением гидравлического пресса (клепальной машины) для образования второй головки. Мелкие заклепки (малого диаметра — меньше 8 мм) ставятся в холодном состоянии (авиационные конструкции).Любое заклепочное соединение работает на 4 вида деформации:-срез заклепок;-срез листа;-разрыв листа;-смятие заклепок;Условия прочности по каждому из видов:1) условие прочности заклепки на перерезывание в таком виде: Рис.1. Передача давлений на стержень заклепки.Чтобы вычислить это условное напряжение смятия, необходимо разделить силу, приходящуюся на заклепку, на площадь диаметрального сечения ВСС'В'. Эта площадь представляет собой прямоугольник, одной стороной которого служит диаметр заклепки, другая же равна толщине листа, передающего давление на стержень заклепки. 45 Кручение: общая картина деформации: скручивающие и крутящие моменты, эпюра крутящих моментов. Кручением называется такой вид деформации, при котором в поперечном сечении стержня возникает лишь один силовой фактор — крутящий момент Мz. Крутящий момент по определению равен сумме моментов внутренних сил относительно продольной оси стержня Oz. Нормальные силы, параллельные оси Oz, вклада в крутящий момент не вносят. С силами, лежащими в плоскости поперечного сечения стержня (интенсивности этих сил — касательные напряжения
47 Деформации бруса круглого сечения. Жесткость при кручении. Эпюра углов закручивания. В любом круговом слое поперечного сечения скручиваемого стержня возникают касательные напряжения
Если в круговом слое скручиваемого стержня обнаружена сдвиговая деформация, то в нем должны возникнуть касательные напряжения, которые по закону Гука составлют τ=Gγ или τ=Gρθ. В центре сеченя напряжения отсутствуют.Относительный угол закручивания пропорционален крутящему моменту в сечении и обратно пропорционален жесткости сечения скручиваемого стержня GIp.Для обеспечения необходимой жесткости производится проверка по условию жесткости вида θmax = Tmax/ (GIp) ≤θadm. Нормативные значения θadm находятся в пределах 0,15 – 2 град/м. 49. Главные напряжения, расчеты на прочность и жесткость, условие прочности. Если скручив. cтержень выполнен из пластичного материала, разрушение происходит от чрезмерных сдвиговых деформаций в поперечных сечениях, развивающихся в поверхностных слоях.Расчетное условие имеет вид: тmax=(Tmax/Ip)ρmax=Tmax/Wp≤RsγcRs – расчётное сопротивление материала сдвигу (Rs=(0.55-0.6)R)Если скручивается стержень из хрупкого материала, то воспользуемся второй теорией прочности (теория наибольших относительных удлинений τmax=Tmax/Wp≤Rtγc/(1+ν), где v – коэффициент Пуассона.Условия прочности при кручении: т=Mzmax/Wp≤[т] Θ=Mzmax/GIp2)Проектный расчет (подбор сечений валов)3)Расчет на грузоподъемность, определяется допускаемая величина крутящего момента.Условие жесткости заключается в том, что угол закручивания единицы длины вала не должен превышать определенную величину.Это условие необходимо учитывать, чтобы избежать явл. пружинения при остановке валов.Допускаемый угол закручивания 1 метра вала Фи0:ФИо≥180*Mz/(Пи*GIp)=ФИ 50. Кручение бруса некруглого поперечного сечения: напряжения, деформации, геометрич. Характеристики, эпюра касательных напряжений для бруса прямоугольного поперечного сечения. Для некруглых поперечных сечений гипотеза плоских сечений неприемлима.Поперечные сечения существенно искривлены и в результате существенно изменяется картина распределения напряжений.Отметим некоторые особенности распределения законов напряжений некруглой формы: 1) если поперечное сечение имеет внешние углы, то в них касательные напряжения должны обращаться в 0 2) если нагруженная поверхность бруса при кручении свободна, то касат. Напряжения, направленные по нормали к контуру так же будут = 0.тA = тmax = Mz/Wk Wk = ρ(b в кубе)Для определения наибольших напряжений и деформаций закручивания пользуются решениями Сен-Ванана:τhmax = T/Wt, Δφ = Tl/(GIt)На рис. 4.3 показана, полученная методом теории упругости, эпюра касательных напряжений для бруса прямоугольного сечения. В углах, как видно, напряжения равны нулю, а наибольшие их значения возникают по серединам больших сторон: в точке А A max = здесь необходимо учесть, что b малая сторона прямоугольника.Значения угла закручивания определяется по формуле: где IK = b 4 аналог полярного момента инерции поперечного сечения бруса.Коэффициенты , и зависят от отношения сторон m = h / b, и их значения приведены в табл. 3. Таблица 3
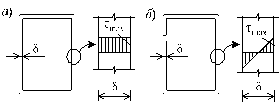
Характерной геометрической особенностью тонкостенных стержней является то, что их толщина существенно (на порядок и более) меньше других геометрических размеров (длиной срединной линии контура поперечного сечения и длины стержня). Характер распределения напряжений по толщине тонкостенного стержня открытого профиля близок к равномерному (рис. 4.7, б), а замкнутого профиля меняется по линейному закону, как это показано на рис. 4.7, а. Откуда следует, что напряжения в поперечных сечениях открытого профиля практически не изменятся, если профиль сечения распрямить. Иначе говоря, напряжения в криволинейном открытом профиле будут примерно такими же, как и в прямом.Обращаясь к формулам (4.14), (4.16) и при предельном переходе где MK (i) доля крутящего момента, соответствующего i му участку: где угловое перемещение, единое для всех участков: Из условия равновесия сил по оси z выделенного элемента длиной dz (4.9) легко установить, что по контуру сечения произведение является постоянной величиной. С учетом данного обстоятельства, выражение примет вид: где Для вывода выражения для угла закручивания воспользуемся энергетическими соображениями. Энергия, накопленная в элементарном объеме с размерами , dz, ds за счет деформаций чистого сдвига, равна:
Приравнивая оба выражения из и получим: Если является постоянной по контуру, будем иметь:
52. Потенциальная энергия при кручении. Потенциальная энергия деформации при кручении определяется подобно тому, как это делалось при растяжении и сдвиге.Удельная потенциальная энергия деформации при чистом сдвиге определяется из уравнении:
Потенциальная энергия деформации U определится из уравнения путем интегрирования по объему:
При этом учитывалось, что
53. Статически неопределимые задачи при расчетах на кручение. Системы, в которых количество наложенных связей больше, нежели число независимых уравнений равновесия,называются статически неопределимыми. По сравнению со статически определимыми системами, в статически неопределимых системах имеются дополнительные связи, которые называются лишними. Термин “лишние связи” является условным. Эти связи являются лишними с точки зрения расчетных предпосылок. В действительности эти связи создают дополнительные резервы для конструкций, как в плане обеспечения её жесткости, так и прочности.На рис. 2.5, а изображен кронштейн, состоящий из двух стержней, шарнирно скрепленных между собой. В связи с тем, что на конструкцию действует лишь вертикальное усилие Р, а система является плоской (т.е. все элементы конструкции и вектор внешних сил лежат в одной плоскости), получается, что усилия в стержнях легко определяются из условий равновесия узла А, т.е. x = 0, y = 0. Раскрывая эти уравнения, получаем замкнутую систему линейных уравнений относительно неизвестных усилий N 1 и N 2 в которой количество уравнений равно количеству неизвестных: N 1 N 2 sin = 0; N 2 cos Р = 0.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 966; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.012 с.) |




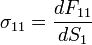 и т.д.
и т.д.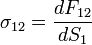 и т.д.
и т.д.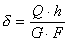 ,
,
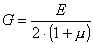 .
.

 .
.
 обусловлена касательным напряжением
обусловлена касательным напряжением  , а деформации
, а деформации  и
и  — соответственно напряжениями
— соответственно напряжениями  и
и  . Между соответствующими касательными напряжениями и угловыми деформациями для линейно-упругого изотропного тела существуют пропорциональные зависимости
. Между соответствующими касательными напряжениями и угловыми деформациями для линейно-упругого изотропного тела существуют пропорциональные зависимости 


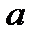 - абсолютный сдвиг,
- абсолютный сдвиг,  - относительный сдвиг.С деформацией сдвига мы встречаемся при резании ножницами металла, при работе различных соединений (резьбовых, шлицевых, шпоночных).Условие прочности при сдвиге (срезе) имеет вид
- относительный сдвиг.С деформацией сдвига мы встречаемся при резании ножницами металла, при работе различных соединений (резьбовых, шлицевых, шпоночных).Условие прочности при сдвиге (срезе) имеет вид  .
.

 зависит от материала и вида соединения. Для неразъемных заклепочных соединений из деформируемых алюминиевых сплавов можно принять
зависит от материала и вида соединения. Для неразъемных заклепочных соединений из деформируемых алюминиевых сплавов можно принять  -в случае неподвижных соединений;
-в случае неподвижных соединений; Помимо среза заклепкам и соединяемым листам в конструкции угрожают и иные опасности.На рис.1 указана примерная схема передачи давлений на стержень заклепки. Закон распределения этих давлений по цилиндрической поверхности нам неизвестен; он во многом зависит от неправильностей формы заклепочного отверстиями стержня, вызванных условиями изготовления конструкции. Поэтому расчет производится условно. Принято считать, что неравномерное давление, передающееся на поверхность заклепки от листа, распределяется равномерно по диаметральной плоскости сечения заклепки. При этом напряжение по этой диаметральной плоскости оказывается примерно равным наибольшему сминающему напряжению
Помимо среза заклепкам и соединяемым листам в конструкции угрожают и иные опасности.На рис.1 указана примерная схема передачи давлений на стержень заклепки. Закон распределения этих давлений по цилиндрической поверхности нам неизвестен; он во многом зависит от неправильностей формы заклепочного отверстиями стержня, вызванных условиями изготовления конструкции. Поэтому расчет производится условно. Принято считать, что неравномерное давление, передающееся на поверхность заклепки от листа, распределяется равномерно по диаметральной плоскости сечения заклепки. При этом напряжение по этой диаметральной плоскости оказывается примерно равным наибольшему сминающему напряжению  в точке А поверхности заклепки.
в точке А поверхности заклепки. 
 Для определения крутящих моментов в сечениях пользуются методом сечений. Намечают участки бруса, рассекают его вооброжаемой плоскостью, мысленно отрбрасывают одну часть. К другой части прикладывают в сечении неизвестный крутящий момент, направляя его по ходу часовой стрелки и составляют уравнение равновесия, из которого находят значение Т.Положительными принимают скручивающие моменты, если они поворачивают отсеченную часть бруса против хода часовой стрелки. Знак крутящего момента бруса значения не имеет.Условимся считать Mz положительным, если со стороны отброшенной части стержня видим его направленным против часовой стрелки (рис. 2). Это правило проиллюстрировано на рис. 1 и в указанном соотношении, где крутящий момент Мz принят положительным. Численно крутящий момент равен сумме моментов внешних сил, приложенных к отсеченной части стержня, относительно оси Ог
Для определения крутящих моментов в сечениях пользуются методом сечений. Намечают участки бруса, рассекают его вооброжаемой плоскостью, мысленно отрбрасывают одну часть. К другой части прикладывают в сечении неизвестный крутящий момент, направляя его по ходу часовой стрелки и составляют уравнение равновесия, из которого находят значение Т.Положительными принимают скручивающие моменты, если они поворачивают отсеченную часть бруса против хода часовой стрелки. Знак крутящего момента бруса значения не имеет.Условимся считать Mz положительным, если со стороны отброшенной части стержня видим его направленным против часовой стрелки (рис. 2). Это правило проиллюстрировано на рис. 1 и в указанном соотношении, где крутящий момент Мz принят положительным. Численно крутящий момент равен сумме моментов внешних сил, приложенных к отсеченной части стержня, относительно оси Ог  Кручением называется простой вид сопротивления, при котором к брусу (валу) прикладываются внешние пары сил в плоскостях, совпадающих с поперечным сечением вала, а в последних возникает только внутренний крутящий момент.Рассмотрим расчетную схему вала, нагруженного двумя сосредоточенными моментами М и 2М и распределенными по длине: m, рис.2.Методика построения эпюры аналогична только что рассмотренной методике при растяжении-сжатии.
Кручением называется простой вид сопротивления, при котором к брусу (валу) прикладываются внешние пары сил в плоскостях, совпадающих с поперечным сечением вала, а в последних возникает только внутренний крутящий момент.Рассмотрим расчетную схему вала, нагруженного двумя сосредоточенными моментами М и 2М и распределенными по длине: m, рис.2.Методика построения эпюры аналогична только что рассмотренной методике при растяжении-сжатии.
 , которые для цилиндрического стержня можно определить по формуле
, которые для цилиндрического стержня можно определить по формуле  . Данное выражения явл. уравнением для построения графика, т.е. эпюры касательных напряжений в любом радиальном направлении круглого сечения.
. Данное выражения явл. уравнением для построения графика, т.е. эпюры касательных напряжений в любом радиальном направлении круглого сечения. 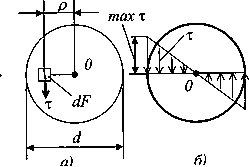
 — погонный угол закручивания стержня, который остается пока неизвестным. Для его нахождения обратимся к условию статики, записав его в более удобной для данного случая форме (рис. 6, a)
— погонный угол закручивания стержня, который остается пока неизвестным. Для его нахождения обратимся к условию статики, записав его в более удобной для данного случая форме (рис. 6, a) 
 , где WК = b 3 аналог полярного момента сопротивления поперечного сечения прямоугольного бруса; в точке В B max ,
, где WК = b 3 аналог полярного момента сопротивления поперечного сечения прямоугольного бруса; в точке В B max , , (4.16)
, (4.16)

 Ðèñ. 4.7
Ðèñ. 4.7
 , получим:
, получим:  ;
; 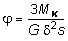 , где толщина профиля; s длина контура профиля; l длина стержня.В случае, если тонкостенный незамкнутый профиль является составным (рис. 4.8) и не может быть развернут в вытянутый прямоугольник, воспользовавшись почленной аналогией, легко определить выражения напряжений на i ом произвольном участке:
, где толщина профиля; s длина контура профиля; l длина стержня.В случае, если тонкостенный незамкнутый профиль является составным (рис. 4.8) и не может быть развернут в вытянутый прямоугольник, воспользовавшись почленной аналогией, легко определить выражения напряжений на i ом произвольном участке:  , (4.18)
, (4.18)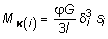 ,
, .рассмотрим брус, имеющий поперечное сечение в форме замкнутого тонкостенного профиля (рис. 4.9). Выделим на контуре элементарный участок длиной ds и выразим крутящий момент через напряжения , выполняя операцию контурного интегрирования получим:
.рассмотрим брус, имеющий поперечное сечение в форме замкнутого тонкостенного профиля (рис. 4.9). Выделим на контуре элементарный участок длиной ds и выразим крутящий момент через напряжения , выполняя операцию контурного интегрирования получим:  . (4.20)
. (4.20) ,
, представляет собой удвоенной площадь, ограниченную срединной линией контура сечения.Из (4.21) наибольшее напряжение определяется по формуле:
представляет собой удвоенной площадь, ограниченную срединной линией контура сечения.Из (4.21) наибольшее напряжение определяется по формуле:  . (4.22)
. (4.22) .С учетом последнее выражение можно представить в виде:
.С учетом последнее выражение можно представить в виде: .С другой стороны, работу внешних сил можно представить в виде:
.С другой стороны, работу внешних сил можно представить в виде:  .
. ,
, ,
, .
.
 .
.
 . В брусе постоянной жесткости GIp при действии постоянного по длине крутящего момента, имеем
. В брусе постоянной жесткости GIp при действии постоянного по длине крутящего момента, имеем .
.
 Если конструкцию кронштейна усложнить, добавив еще один стержень (рис. 2.5, б), то усилия в стержнях N 1, N 2 и N 3 прежним способом определить уже не удастся, т.к. при тех же двух уравнениях равновесия (2.16) имеются уже три неизвестных усилия в стержнях. В таких случаях говорят, что система один раз статически неопределима. Разность между числом неизвестных усилий и количеством независимых (значащих) уравнений равновесия, связывающих эти усилия, называется степенью статической неопределимости рассматриваемой системы.В общем случае под n раз статически неопределимой системой понимается система, в которой число неизвестных внешних опорных реакций и внутренних усилий превышает число независимых и значащих уравнений равновесия на n единиц. Решение статически неопределимых задач методом сил проводится в такой последовательности.1. Устанавливается степень статической неопределимости системы как разность между числом искомых неизвестных усилий и числом независимых уравнений равновесия. При этом учитывается, что простой шарнир, соединяющий два стержня системы, уменьшает степень статической неопределимости на единицу, так как снимает одну связь, препятствующую повороту одной части системы относительно другой. Тем самым простой шарнир позволяет добавить к уравнениям равновесия всей системы уравнение равновесия присоединенной этим шарниром части системы.2. Из заданной статически неопределимой системы выделяется основная система путем удаления лишних связей и внешней нагрузки.В качестве лишних могут быть выбраны различные связи. Поэтому для одной и той же статически неопределимой системы можно получить сколько угодно основных систем. Но любая основная система должна быть обязательно геометрически неизменяемой и статически определимой.Нельзя выбирать в качестве основной и мгновенно геометрически изменяемую систему, потому что в такой системе при любой сколь угодно малой нагрузке усилия получаются бесконечно большими или неопределенными.3. Изображается соответствующая выбранной основной эквивалентная система, в которой взамен снятых лишних связей и в их направлении приложены силы Xi, если связи препятствовали линейному перемещению, и пары Xk, если они исключали повороты сечений.4. Составляются канонические уравнения метода сил.5. Вычисляются коэффициенты канонических уравнений аналитически
Если конструкцию кронштейна усложнить, добавив еще один стержень (рис. 2.5, б), то усилия в стержнях N 1, N 2 и N 3 прежним способом определить уже не удастся, т.к. при тех же двух уравнениях равновесия (2.16) имеются уже три неизвестных усилия в стержнях. В таких случаях говорят, что система один раз статически неопределима. Разность между числом неизвестных усилий и количеством независимых (значащих) уравнений равновесия, связывающих эти усилия, называется степенью статической неопределимости рассматриваемой системы.В общем случае под n раз статически неопределимой системой понимается система, в которой число неизвестных внешних опорных реакций и внутренних усилий превышает число независимых и значащих уравнений равновесия на n единиц. Решение статически неопределимых задач методом сил проводится в такой последовательности.1. Устанавливается степень статической неопределимости системы как разность между числом искомых неизвестных усилий и числом независимых уравнений равновесия. При этом учитывается, что простой шарнир, соединяющий два стержня системы, уменьшает степень статической неопределимости на единицу, так как снимает одну связь, препятствующую повороту одной части системы относительно другой. Тем самым простой шарнир позволяет добавить к уравнениям равновесия всей системы уравнение равновесия присоединенной этим шарниром части системы.2. Из заданной статически неопределимой системы выделяется основная система путем удаления лишних связей и внешней нагрузки.В качестве лишних могут быть выбраны различные связи. Поэтому для одной и той же статически неопределимой системы можно получить сколько угодно основных систем. Но любая основная система должна быть обязательно геометрически неизменяемой и статически определимой.Нельзя выбирать в качестве основной и мгновенно геометрически изменяемую систему, потому что в такой системе при любой сколь угодно малой нагрузке усилия получаются бесконечно большими или неопределенными.3. Изображается соответствующая выбранной основной эквивалентная система, в которой взамен снятых лишних связей и в их направлении приложены силы Xi, если связи препятствовали линейному перемещению, и пары Xk, если они исключали повороты сечений.4. Составляются канонические уравнения метода сил.5. Вычисляются коэффициенты канонических уравнений аналитически