
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка влияния факторов на зависимую переменную (коэффициенты эластичности, бета коэффициенты).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Чтобы исследовать влияние факторов X1, X2, … Xp на результирующий признак Y, рассмотрим линейную множественную модель:
Коэффициенты регрессии показывают, на сколько единиц изменился результирующий признак Y, при увеличении соответственного фактора на 1 ед., при неизменном значении остальных факторных, т. к. величины коэффициентов aj зависят от единиц измерения переменных Хj, то с их помощью нельзя сравнивать влияние каждой факторной переменной Xj на результирующий признак Y. Поэтому вводят в рассмотрение безразмерные коэффициенты: коэффициенты эластичности, бета- и дельта- коэффициенты. 1). Средние коэффициенты эластичности в случае линейной модели определяются формулами:
где Средний коэффициент эластичности Эj показывает, на сколько процентов изменится в среднем переменная Y, если факторная переменная Xj увеличится на 1%, при неизменных значениях остальных факторов, закрепленных на их средних уровнях. 2). Бета - коэффициенты определяются формулами:
где Бета- коэффициенты показывает, на какую часть своего стандартного отклонения изменится в среднем результирующая переменная Y при увеличении только фактора Хj на одно его стандартное отклонение. 3). Дельта - коэффициенты определяются формулами
Замечание: значение показывающие абсолютные доли влияния факторов Хj на результирующую переменную. Т. к., коэффициенты эластичности, бета- и дельта- коэффициенты являются безразмерными, их можно сравнивать между собой и ранжировать таким образом факторы по силе их воздействия на результат.
20. Понятие о мультиколлинеарности. Методы устранения мультиколлинеарности (перечислить методы, описать любой метод). Наибольшие затруднения в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторных переменных, когда более чем два фактора связаны между собой линейной зависимостью.
Мультиколлинеарностью для линейной множественной регрессии называется наличие линейной зависимости между факторными переменными, включёнными в модель.
Мультиколлинеарность – нарушение одного из основных условий, лежащих в основе построения линейной модели множественной регрессии.
Мультиколлинеарность в матричном виде – ϶ᴛᴏ зависимость между столбцами матрицы факторных переменных Х:
Чем сильнее мультиколлинеарность факторных переменных, тем менее надежной будет оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов.
Методы устранения мультиколлинеарности 1) Исключение переменных из модели - метод дополнительной регрессии Для выявления списка зависимых регрессоров проводится дополнительная регрессия – регрессия каждого регрессора X на оставшиеся регрессоры. Стандартным способом, на основе F-статистики, проверяется статистическая значимость коэффициентов детерминации дополнительных регрессий.
где n- число наблюдений, а k – число регрессоров в первоначальной спецификации регрессионной модели. Статистика Fимеет распределение Фишера с параметрами Если коэффициент детерминации (Rв квадрате) незначим, то регрессор Х не приводит к мультиколлинеарности и его оставляют в списке переменных модели. В противном случае его рекомендуется исключить из списка.
2) методы, использующие внешнюю информацию Под внешней информацией понимаются теоретические ограничение (например, некоторые допущения, касающиеся параметров модели или некоторой связи между ними) и внешние эмпирические оценки (например, полученные по перекрестным статистическим данным из другой выборки). Увеличение числа наблюдений приводит к снижению мультиколлинеарности и к уменьшению теоретических дисперсий коэффициентов регрессии.
3) переход к смещенный методам оценивания
В условиях мультиколлинеарности дисперсии несмещенных оценок могут оказаться слишком большими. Поэтому иногда целесообразно отказаться от требований несмещенности. Один из таких подходов, названный гребневой регрессией, основан на «подправленных» МНК-оценках вида:
Понятие статистической процедуры оценивания параметров эконометрической модели. Требования к наилучшей статистической процедуре: несмещённость и минимальные дисперсии оценок параметров.
Оценкой ân параметра a называют всякую функцию результатов наблюдений над случайной величиной X (иначе — статистику), с помощью которой судят о значениях параметра a. Статистические проверки параметров регрессии основаны на непроверяемых предпосылках распределения случайной величины. Они носят лишь предварительный характер. После построения уравнения регрессии проводится проверка наличия у оценок тех свойств, которые предполагались. Связано это с тем, что оценки параметров регрессии должны отвечать определенным критериям: быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции. В отличие от параметра, его оценка ã n — величина случайная. «Наилучшая оценка» ã n должна обладать наименьшим рассеянием относительно оцениваемого параметра a, например, наименьшей величиной математического ожидания квадрата отклонения оценки от оцениваемого параметра М(ã - a)2. Оценка â n параметра a называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т. е. М(ã) = a. В противном случае оценка называется смещенной. Если это равенство не выполняется, то оценка ã, полученная по разным выборкам, будет в среднем либо завышать значение a (если М(ã) > a, либо занижать его (если М(ã) < 0). Таким образом, требование несмещенности гарантирует отсутствие систематических ошибок при оценивании. Оценка â n параметра a называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру:
В случае использования состоятельных оценок оправдывается увеличение объема выборки, так как при этом становятся маловероятными значительные ошибки при оценивании. Поэтому практический смысл имеют только состоятельные оценки. Несмещенная оценка ã n параметра a называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра a, вычисленных по выборкам одного и того же объема n. Так как для несмещенной оценки M(ã n - a)2 есть ее дисперсия Для нахождения оценок параметров (характеристик) генеральной совокупности используется ряд методов. Указанные критерии оценок (несмещенность, состоятельность, эффективность) обязательно учитываются при разных способах оценивания.
Предпосылки применения МНК. (условия Гаусса-Маркова). Всего их 5 1. Математическое ожидание случайного отклонения εi рав- но нулю: M(εi) = 0 для всех наблюдений. Данное условие означает, что случайное отклонение в сред- нем не оказывает влияния на зависимую переменную. В каждом конкретном наблюдении случайный член может быть либо поло- жительным, либо отрицательным, но он не должен иметь система- тического смещения. Отметим, что выполнимость М(εi) = 0 влечет выполнимость M(Y приX=xi) = β0 + β1*xi.
2. Дисперсия случайных отклонений εi постоянна: D(εi) = D(εj) = σ2 для любых наблюдений i и j. Данное условие подразумевает, что, несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть либо большим, либо меньшим, не должно быть некой априор- ной причины, вызывающей большую ошибку (отклонение). Выполнимость данной предпосылки называется гомоскеда стичностью (постоянством дисперсии отклонений). Невыполни- мость данной предпосылки называется гетероскедастичностью (не- постоянством дисперсий отклонений). данную предпосылку можно переписать в форме: М(ε 2i) = σ2.
3. Случайные отклонения εi и εj являются независимыми друг от друга для i ≠ j. Выполнимость данной предпосылки предполагает, что от- сутствует систематическая связь между любыми случайными от- клонениями. Другими словами, величина и определенный знак лю- бого случайного отклонения не должны быть причинами величины и знака любого другого отклонения. 4. Случайное отклонение должно быть независимо от объяс- няющих переменных. Обычно это условие выполняется автоматически, если объ- ясняющие переменные не являются случайными в данной модели. Данное условие предполагает выполнимость следующего со- отношения: cov(εi, xi) = M((εi –M(εi))⋅(xi – M(xi))) = i i = M(εi (xi – M(xi))) = M(εi xi) – M(εi)⋅M(xi) = M(εi x i) = 0. Следует отметить, что выполнимость данной предпосылки не столь критична для эконометрических моделей.
5. Модель является линейной относительно параметров.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2435; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.86.30 (0.007 с.) |


 j = 1, 2, …, p,
j = 1, 2, …, p, - выборочные средние признаков Xj и Y.
- выборочные средние признаков Xj и Y.
 - выборочные средние квадратичные отклонения признаков Xj и Y.
- выборочные средние квадратичные отклонения признаков Xj и Y. где
где  - соответствующие выборочные коэффициенты парной корреляции. Дельта-коэффициенты показывают долю влияния каждого фактора в суммарном воздействии на результирующую переменную.
- соответствующие выборочные коэффициенты парной корреляции. Дельта-коэффициенты показывают долю влияния каждого фактора в суммарном воздействии на результирующую переменную. <0,
<0,  <0 – ухудшает качество модели и должен быть исключен.
<0 – ухудшает качество модели и должен быть исключен.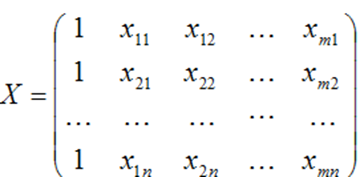
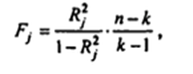



 , то эффективность является решающим свойством, определяющим качество оценки.
, то эффективность является решающим свойством, определяющим качество оценки.


