
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение фиктивных переменных при исследовании сезонных колебаний: спецификация модели, экономический смысл параметров при фиктивных переменных. (15)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Термин “фиктивные переменные” используется как противоположность “значащим” переменным, показывающим уровень количественного показателя, принимающего значения из непрерывного интервала. Как правило, фиктивная переменная — это индикаторная переменная, отражающая качественную характеристику. Чаще всего применяются бинарные фиктивные переменные, принимающие два значения, 0 и 1, в зависимости от определенного условия. Например, в результате опроса группы людей 0 может означать, что опрашиваемый - мужчина, а 1 - женщина. Могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Регрессионная модель, включающая в качестве фактора (факторов) фиктивную переменную, называется регрессионной моделью с переменной структурой. Рассмотрим временной ряд Xi j, где i — это номер сезона (периода времени внутри года, напри мер, месяца или квартала);
j — номер года, j = Количество уровней исходного ряда равно L × m = n. Число сезонных фиктивных переменных в регрессионной модели всегда должно быть на единицу меньше сезонов внутри года, т. е. должно быть равно величине L − 1. При моделировании годовых данных регрессионная модель, помимо фактора времени, должна содержать одиннадцать фиктивных компонент (12 − 1). Каждому из сезонов соответствует определенное сочетание фиктивных переменных. Сезон, для которого значения всех фиктивных переменных равны нулю, принимается за базу сравнения. Для остальных сезонов одна из фиктивных переменных принимает значение, равное единице. Если имеются поквартальные данные, то значения фиктивных переменных D 1, D 2, D 3 будут принимать следующие значения для каждого из кварталов
Общий вид регрессионной модели с переменной структурой в данном случае будет иметь вид: yt =β0 +β1 × t +δ2 × D2 +δ3 × D3 +δ4 × D4 +εt Построенная модель регрессии является разновидностью аддитивной модели временного ряда. Базисным уравнением исследуемой регрессионной зависимости будет являться уравнение тренда для первого квартала: y =β +β × t +ε Тогда общий вид модели регрессии с переменной структурой будет иметь вид: yt=β0+ β1*t+δ2*D2+δ3*D3+δ4*D4+εt. Данная модель регрессии представляет собой одну из разновидностей аддитивной модели временного ряда. На основе общей модели регрессии с переменной структурой можно составить базисную модель или модель тренда для первого квартала: yt=β0+ β1*t+εt. Также на основе общей модели регрессии с переменной структурой можно составить частные модели регрессии: 1) частная модель регрессии для второго квартала: yt=β0+ β1*t+δ2+εt; 2) частная модель регрессии для третьего квартала: yt=β0+ β1*t+δ3+εt; 3) частная модель регрессии для четвёртого квартала: yt=β0+ β1*t+δ4+εt. Данные частные модели регрессии отличаются друг от друга только на величину свободного члена δi. Коэффициент β1 характеризует среднее абсолютное изменение уровней временного ряда под влиянием основной тенденции. Сезонная компонента для каждого сезона рассчитывается как разность между средним значением свободных членов всех частных моделей регрессий и значением постоянного члена одной из моделей. Среднее значение свободных членов всех частных моделей регрессий рассчитывается по формуле:
Для поквартальных данных оценка сезонных отклонений осуществляется по формулам: 1) оценка сезонного отклонения для первого квартала:
2) оценка сезонного отклонения для второго квартала:
3) оценка сезонного отклонения для третьего квартала:
4) оценка сезонного отклонения для четвёртого квартала:
Сумма сезонных отклонений должна равняться нулю.
51. Проблема мультиколлинеарности в моделях множественной регрессии. Признаки мультиколлинеарности (15 баллов). Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных, которая приводит к линейной зависимости нормальных уравнений. Мультиколлинеарность может проявляться в двух формах: 1. Функциональной – определитель матрицы X’Xравен нулю. Это приводит к невозможности решения соответствующей системы нормальных уравнений и получения оценок параметров регрессионной модели; 2. Стохастической, когда между хотя бы двумя объясняющими переменными существует тесная корреляционная связь. В этом случае определитель матрицы X’X не равен нулю, но очень мал. Экономическая интерпретация параметров уравнения регрессии при этом затруднена, так как некоторые из его коэффициентов могут иметь неправильные с точки зрения экономической теории знаки и неоправданно большие значения. Оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменениями объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования. Существует несколько способов для определения наличия или отсутствия мультиколлинеарности: 1. Анализ матрицы коэффициентов парной корреляции. Явление мультиколлинеарности в исходных данных считают установленным, если коэффициент парной корреляции между двумя переменными больше 0,8. 2. Исследование матрицы X’X. Если определитель матрицы близок к нулю, это свидетельствует о наличии мультиколлинеарности.
Свойства оценок МНК. Для того чтобы регрессионный анализ, основанный на МНК давал наилучшие результаты, должны выполняться условия Гаусса-Маркова. Если все предпосылки выполняются, то оценки, полученные по МНК, будут обладать свойствами а). несмещённости, б). эффективности, в). состоятельности. А). Несмещённость оценки означает, что матем.ожид. остатков равно нулю. Если оценки обладают свойством несмещённости, то их можно сравнивать по разным исследованиям. Б). Оценки считаются эффективными, если они характеризуются наименьшей дисперсией. В). Состоятельность оценок характеризует увеличение их точности с увеличением объёма выборки.
53. Спецификация и оценивание МНК эконометрических моделей нелинейных по параметрам. (15 баллов). В моделях, нелинейных по параметрам, например, степенных или показательных, непосредственное применение МНК для их оценки невозможно, так как необходимым условием применимости МНК является линейность по коэффициентам уравнения регрессии. В данном случае преобразованием, которое приводит уравнение регрессии к линейному виду, является логарифмирование. После приведения модели к линейному виду, можно применять обычный МНК для оценки её параметров. Пример. Рассмотрим уравнение
т.е. параметр β представляет собой эластичность переменной Y по переменной Х. уравнение не является линейным. Прологарифмируем обе части данного уравнения: ln(Y)=ln(A)+ βln(X)=α+βln(X), гдеα=ln(A). Уравнение линейно относительно логарифмов переменных, поэтому можно применить обычный МНК.
54. Способы корректировки автокорреляции (авторегрессионные модели первого порядка) (15 баллов). Рассмотрим авторегрессионную модель первого порядка, в которой значение возмущения ɛ определяется через его лаговое значение первого порядка. В этом случае спецификация регрессионной модели с регрессией случайного возмущения имеет вид:
где
Необходимо определить начальные условия модели. Начальные условия модели определяются нормальной случайной величиной Корректирующий множитель
55. Способы корректировки гетероскедастичности. Взвешенный метод наименьших квадратов (15 баллов). При наличии гетероскедастичности в остатках рекомендуется традичионный МНК заменить обобщенным методом наименьших квадратов (ОМНК). Этот метод применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии. Будем считать, что среднее значение остаточных величин равно нулю. В то же время дисперсия их не остается неизменной для различных значений фактора, а пропорциональна некоторой величине К. В общем виде уравнение регрессии примет вид По отношению к обычной регрессии уравнение с новыми, преобразованными переменными представляет собой взвешенную регрессию, в которой переменные X и Y взяты с весами Оценка параметров уравнения с преобразованными переменными приводит к взвешенному методу наименьших квадратов, для которых необходимо минимизировать сумму квадратов отклонений:
ОМНК-оценка вектора А равна A=
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 698; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

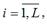 (L — число сезонов в году);
(L — число сезонов в году);
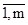 (m — общее количество лет).
(m — общее количество лет).
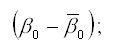



 , где А и β – параметры модели. Параметр А степенной модели представляет собой значение эндогенной переменной, полученное при единичном значении регрессора. Для того, чтобы дать экономическую интерпретацию параметру β данной модели, продифференцируем уравнение по переменной Х:
, где А и β – параметры модели. Параметр А степенной модели представляет собой значение эндогенной переменной, полученное при единичном значении регрессора. Для того, чтобы дать экономическую интерпретацию параметру β данной модели, продифференцируем уравнение по переменной Х:

 , t – случайные возмущения авторегрессионного уравнения – независимые нормально распределенные случайные величины:
, t – случайные возмущения авторегрессионного уравнения – независимые нормально распределенные случайные величины: 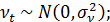
 – коэффициент авторегрессии (параметр модели) (-1<
– коэффициент авторегрессии (параметр модели) (-1< 
 служит для обеспечения гомоскедастичности случайных возмущений.
служит для обеспечения гомоскедастичности случайных возмущений.


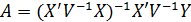 , где
, где , V=
, V=  , X=
, X= 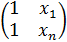 , Y=
, Y= 



