
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отражение в модели влияния неучтённых факторов. Предпосылки теоремы Гаусса-Маркова(15)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для учета случайного характера экономических процессов, модель записывают в виде: Y = f(X) + ε (1) где: Y – эндогенная переменная X – вектор предопределенных переменных f(X) – детерминированная математическая функция, определяющая закономерность между эндогенной и предопределенными переменными ε – случайная величина, учитывающая влияние неучтенных факторов и индивидуальные особенности конкретного объекта (случайное возмущение). Модель (1) называют эконометрической моделью. Правая часть (1) называется обобщенной функциональной или регрессионной зависимостью. При составлении модели случайные возмущения присутствуют только в поведенческих уравнениях эконометрической модели. В уравнениях тождествах они отсутствуют. Рассеянные вокруг нуля случайные возмущения отражают влияние на текущие эндогенные переменные этой модели неучтённых факторов.
Случайные возмущения сохраняются в приведенной форме модели. Их вычисление производится по формуле: ε= A-1 Замечание. Необходимость учета в моделях влияния случайных возмущений является четвертым принципом спецификации эконометрических моделей 45. Оценивание линейной модели множественной регрессии методом наименьших квадратов (МНК) в Excel с использованием сервиса Поиск решения. (15 баллов) Множественная регрессия позволяет построить и проверить модель линейной связи между зависимой (эндогенной) и несколькими независимыми (экзогенными) переменными: y = f(x1,...,xр), где у - зависимая переменная (результативный признак); х1,...,хр - независимые переменные (факторы). В Exel существует несколько способов решения задач через МНК (Поиск решений, мастер диаграмм, матричные функции, анализ данных и тд) Остановимся подробнее на функции «Поиск решений». Она находится во вкладке данные- поиск решений. Поиск решения- это надстройка Exel, которая позволяет решать оптимизационные задачи. Основные параметры диалогового окна: Установить целевую ячейку Изменяя ячейки Ограничения
46. Оценка параметров парной регрессионной модели методом наименьших квадратов (15 баллов).
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров a и b, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических)
Для того чтобы найти минимум функции, надо вычислить частные производные по каждому из параметров a и b и приравнять их к нулю. Тогда мы получаем следующую систему нормальных уравнений для оценки параметров a и b
Решая систему нормальных уравнений либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров a и b. Можно воспользоваться следующими формулами для a и b:
Эта формула получена из первого уравнения системы, если все его члены разделить на n:
Таким образом: Свойство несмещенностиоценок состоит в том, что математическое ожидание оценки должно быть равно истинному значению параметра. Свойство состоятельностиоценок состоит в том, что с увеличением наблюдений оценка становится более надежной в вероятностном смысле. Оценка называется эффективной, если она имеет минимальную дисперсию по сравнению с любыми другими оценками этого параметра в классе выбранных процедур.
47. Понятие о мультиколлинеарности. Методы устранения мультиколлинеарности (перечислить методы, описать любой метод) (15 баллов).
Множественная регрессия позволяет построить и проверить модель линейной связи между зависимой (эндогенной) и несколькими независимыми (экзогенными) переменными: y = f(x1,...,xр), где у - зависимая переменная (результативный признак); х1,...,хр - независимые переменные (факторы). Множественная линейная регрессионная модель имеет вид: y=a+b1x1+b2x2+…+bpxp+ε Поскольку одним из условий построения уравнения множественной регрессии является независимость действия факторов, коллинеарность факторов нарушает это условие. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. Признаки мультиколлинеарности. 1. В модели с двумя переменными одним из признаков мультиколлинеарности является близкое к единице значение коэффициента парной корреляции. Если значение хотя бы одного из коэффициентов парной корреляции больше, чем 0,8, то мультиколлинеарность представляет собой серьезную проблему. Методы устранения: · предварительного центрирования. Суть метода сводится к тому, что перед нахождением параметров математической модели проводится центрирование исходных данных: из каждого значения в ряде данных вычитается среднее по ряду: · Метод дополнительных регрессий · Метод последовательного присоединения
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 805; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.76 (0.006 с.) |

 В общем виде эконометрической модели случайные возмущения отражаются как:
В общем виде эконометрической модели случайные возмущения отражаются как: – вектор-столбец случайных возмущений модели.
– вектор-столбец случайных возмущений модели.
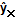 минимальна:
минимальна:

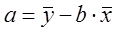
 , где cov(x,y) — ковариация признаков; σх2— дисперсия признака х. Поскольку
, где cov(x,y) — ковариация признаков; σх2— дисперсия признака х. Поскольку  , получим следующую формулу расчета оценки параметра b
, получим следующую формулу расчета оценки параметра b

 . Эта процедура позволяет так развести гиперплоскости условий МНК, чтобы углы между ними были перпендикулярны. В результате этого оценки модели становятся устойчивыми.
. Эта процедура позволяет так развести гиперплоскости условий МНК, чтобы углы между ними были перпендикулярны. В результате этого оценки модели становятся устойчивыми.


