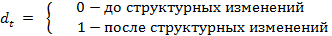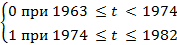Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выявление и устранение аномальных наблюдений во временных рядах.(15)Содержание книги
Поиск на нашем сайте
Выявление аномальных наблюдений – обязательная процедура этапа предварительного анализа данных во временных рядах. Наличие аномальных наблюдений приводит к искажению результатов моделирования. Один из методов диагностики аномальных наблюдений – метод Ирвина. Для всех или только для подозреваемых в аномальности наблюдений вычисляется величина λt:
где
Если рассчитанная величина превышает критическое значение критерия Ирвина λ (определяемое по соответствующей таблице по значениям n-число наблюдений и доверительной вероятности P), то уровень yt считается аномальным. Аномальные наблюдения исключаются из временного ряда и заменяются их расчетными значениями (самый простой способ замены – в качестве нового значения принять среднее из двух соседних значений).
36. Измерение тесноты связи между показателями. Анализ матрицы коэффициентов парной корреляции. (15 баллов). В зависимости от объема выборочной совокупности предлагаются различные методы оценки существенности линейного коэффициента корреляций.
Оценка значимости коэффициента корреляции при малых объемах выборки выполняется с использованием t-критерия Стьюдента. При этом фактическое (наблюдаемое) значение этого критерияопределяется по формуле
Вычисленное по этой формуле значение Если tнабл>tтабл, то полученное значение коэффициента корреляции признается значимым (т.е. нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается). И таким образом делается вывод, что между исследуемыми переменными есть теснаястатистическая взаимосвязь. Если значение rу,х близко к нулю, связь между переменными слабая. Если корреляция между случайными величинами: • положительная, то при возрастании одной случайной величины другая имеет тенденцию в среднем возрастать; • отрицательная, то при возрастании одной случайной величины другая имеет тенденцию в среднем убывать.
Для качественной оценки коэффициента корреляции применяются различные шкалы, наиболее часто — шкала Чеддока. В зависимости от значения коэффициента корреляции связь может иметь одну из оценок: 0,1—0,3 — слабая; 0,3-0,5 — заметная; 0,5—0,7 — умеренная; 0,7—0,9 — высокая; 0,9—1,0 — весьма высокая.
Матрица коэффициентов парной корреляции Коэффициенты парной корреляции используются для измерения силы линейных связей различных пар признаков из их множества. Для множества признаков получают матрицу коэффициентов парной корреляции. Пусть вся совокупность данных состоит из переменной Y = (
На основании данных, содержащихся в этой таблице, вычисляют матрицу коэффициентов парной корреляции R,она симметрична относительно главной диагонали:
Анализ матрицы коэффициентов парной корреляции используют при построении моделей множественной регрессии.
37. Использование фиктивных переменных для определения структурных изменений в экономике (15 баллов). Для определения структурных изменений в экономике используют фиктивные переменные наклона (например, введение новых правовых или налоговых ограничений, изменение политической ситуации и т. д.).
Спецификация регрессионной модели имеет вид:
ПРИМЕР.
Модель расходов на автотранспорт в Европе в период с 1963 по 1982 годы. Замечание. В 1974 году в Европе начался крупный нефтяной кризис, который резко поднял цены на нефтепродукты. В результате в 1974 году резко снизились расходы на автотранспорт, но затем затраты вновь стали расти с прежней скоростью. Для учета этой ситуации вводится фиктивная переменная d, которая равна: d =
Получаем уравнение с помощью «Анализ данных», и, исходя из уравнения, рассчитываем расходы (Y) на автотранспорт за каждый год.
Вывод: в 1974 структурные изменения произошли, снизив заметно расходы на автотранспорт.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1505; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.28.79 (0.006 с.) |

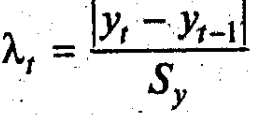 ,
,

 сравнивается с критическим значениемt-критерия, которое берется из таблицы значений t-критерия Стьюдента с учетом заданного уровня значимости αи числа степеней свободы(n - 2).
сравнивается с критическим значениемt-критерия, которое берется из таблицы значений t-критерия Стьюдента с учетом заданного уровня значимости αи числа степеней свободы(n - 2). переменных (факторов)X, каждая из которых содержит n наблюдений. Значения переменных Y и X, содержащиеся в наблюдаемой совокупности, записываются в таблицу
переменных (факторов)X, каждая из которых содержит n наблюдений. Значения переменных Y и X, содержащиеся в наблюдаемой совокупности, записываются в таблицу