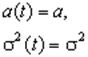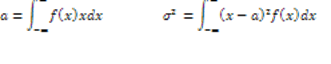Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Что такое логит, тобит, пробит моделиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Модели, которые не поддаются исследованию методами стандартного регрессионного анализа. • ПРОБИТ-МОДЕЛИ — вид эконометрических моделей, которые содержат дихотомические переменные (“все или ничего”). Примеры — модели принятия решений. • ЛОГИТ-МОДЕЛИ — эконометрические модели, в которых зависимая переменная может принимать лишь ограниченное число значений, в простейшем случае — либо 0, либо 1 • ТОБИТ-МОДЕЛИ — вид эконометрических моделей, которые включают переменные, представляющие собой смесь дискретных и непрерывных величин. Пример - модели рынков, на которых часть цен лимитированы, а часть свободны.
Что такое стационарный процесс.
Случайный процесс называется стационарным в строгом (узком) смысле, если его функция распределения любого порядка не изменяется при сдвиге совокупности точек Если приведенное выше условие не выполняется, то процесс называется нестационарным. Нестационарный процесс будет наблюдаться, например, на выходе какого-либо генератора шумов непосредственно после его включения. Из определения стационарного процесса следует, что
т.е. одномерная функция распределения вообще не зависит от времени, а двумерная функция распределения зависят только от разностей времен
а корреляционная функция такого процесса зависит только от одной переменной
случайный процесс называют стационарным в широком смысле, если его среднее значение и дисперсия не зависят от времени, а корреляционная функция зависит только от разности времен
Этапы построения эконометрических моделей. Построение эконометрической модели выполняется в несколько этапов: 1) спецификация модели (подробное описание, определяется список экономических переменных, характеризующих функционирование данного объекта и устанавливается их взаимосвязь) 2) сбор статистической информации об объекте исследования 3) оценка параметров модели (параметризация, настройка) 4) проверка адекватности модели (верификация, проверяется соответствие модели эмпирическим данным)
1. Определение цели исследования. Построение системы показателей, логический отбор факторов. Требования к включаемым в модель факторам: • включение каждого фактора должно быть обосновано теоретически; • целесообразно учитывать только те факторы, которые оказывают существенное влияние на изучаемые показатели, количество включаемых факторов не должно превышать одной трети от длины временного ряда; • между факторами не должно существовать линейной зависимости; две переменные линейно зависимы, если парный коэффициент корреляции между ними по абсолютной величине превышает 0,8. • рекомендуется включать только те факторы, которые могут быть измерены количественно; • не следует включать какой-либо фактор одновременно с образующими его частными факторами.
3. Выбор формы связи изучаемых показателей между собой и отобранными факторами, т.е. - выбор типа эконометрической модели. Сбор исходных данных и анализ информации.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.49.90 (0.009 с.) |

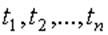 на величину
на величину  , т.е.
, т.е. 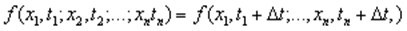 Другими словами, для стационарного процесса функция распределения любого порядка и, следовательно, его характеристики не зависят от положения начала отсчета времени. Стационарность означает статистическую однородность процесса во времени. Физически стационарный случайный процесс представляет собой случайный процесс в установившемся режиме. Физически стационарный случайный процесс представляет собой случайный процесс в установившемся режиме, каковым является, например, шум на выходе усилителя через достаточно большой промежуток времени после его включения.
Другими словами, для стационарного процесса функция распределения любого порядка и, следовательно, его характеристики не зависят от положения начала отсчета времени. Стационарность означает статистическую однородность процесса во времени. Физически стационарный случайный процесс представляет собой случайный процесс в установившемся режиме. Физически стационарный случайный процесс представляет собой случайный процесс в установившемся режиме, каковым является, например, шум на выходе усилителя через достаточно большой промежуток времени после его включения.

 . Отсюда следует, что для стационарного случайного процесса среднее значение и дисперсия являются постоянными величинами, т.е. не зависит от времени
. Отсюда следует, что для стационарного случайного процесса среднее значение и дисперсия являются постоянными величинами, т.е. не зависит от времени