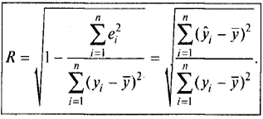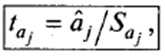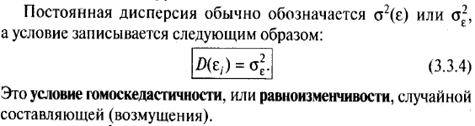Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Адаптивные модели прогнозирования.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гетероскедастичность случайного возмущения (определение). Алгоритм теста Голдфелда-Квандта на наличие или отсутствие гетероскедастичности случайных возмущений в парной регрессионной модели.
Гетероскедастичность случайного возмущения – это нарушение условия гомоскедастичности, или равноизменчивости возмущений означающее, что дисперсия возмущения зависит от значений факторов.
Алгоритм теста Голфелда-Квандта: Данный тест используется для такого типа гетероскедастичности, когда дисперсия остатков возрастает пропорционально квадрату фактора. При этом делается предположение, что случайная составляющая ε распределена нормально.
Чтобы оценить нарушение гомоскедастичности по тесту Голфелда-Квандта, необходимо выполнить следующие шаги: · Упорядочить n наблюдение по мере возрастания переменой X · Исключить d средних наблюдений (d должно быть примерно равно ¼ общего количества наблюдений) · Разделить совокупность на 2 группы (соответственно с малыми и большими значениями фактора X) и определить по каждой из групп уравнение регрессии · Определить остаточную сумму квадратов для первой регрессии · Вычислить отношение
Коэффициент детерминации в парной регрессионной модели: определение, расчетная формула, смысл компонентов формулы, смысл коэффициента детерминации.
Коэффициент детерминации показывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов, т.е. определяет, какая доля вариации признака Y учтена в модели и обусловлена влиянием на него факторов.
Чем ближе R2 к единице, тем выше качество модели.
Коэффициент детерминации как индикатор качества спецификации эконометрической модели.
Коэффициент детерминации показывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов, т.е. определяет, какая доля вариации признака Y учтена в модели и обусловлена влиянием на него факторов.
Чем ближе R2 к единице, тем выше качество модели.
Матричная форма метода наименьших квадратов: спецификация парной регрессионной модели в матричной форме. Уравнение парной регрессии в матричной форме: Y = X·A + ε, где Y – вектор-столбец (nx1) наблюдаемых значений зависимой переменной; X – матрица (nx2) значений факторов; A – вектор-столбец (2x1) неизвестных коэффициентов регрессии; ε – вектор-столбец (nx1) ошибок наблюдений
Параметры системы нормальных уравнений находятся с помощью МНК по формуле: A = (X’·X)-1·X’·Y Для расчета вектора A необходимо: 1. Транспонировать матрицу X => [ ТРАНСП]; 2. Умножить транспонированную матрицу на исходную (X’X) => [МУМНОЖ]; 3. Вычислить обратную матрицу (X’X)-1 => [МОБР]; 4. Умножить обратную матрицу на транспонированную (X’·X)-1·X’ => [МУМНОЖ]; 5. Умножить исходную матрицу на Y (X’·X)-1·X’·Y => [МУМНОЖ]
Линейная модель множественной регрессии. Порядок её оценивания методом наименьших квадратов в Excel. Смысл выходной статистической информации в Анализе данных. Множественная регрессия позволяет построить и проверить модель линейной связи между зависимой (эндогенной) и несколькими независимыми (экзогенными) переменными: y = f(x1,...,xр), где у - зависимая переменная (результативный признак); х1,...,хр - независимые переменные (факторы). Линейное уравнение множественной корреляции: y=a+b1x1+b2x2+…+bpxp+ε.
В Exel существует несколько способов решения задач через МНК (Поиск решений, мастер диаграмм, матричные функции, анализ данных и тд) Необходимый нам «анализ данных» находится во вкладке данные- анализ данных. Инструмент «регрессия» С помощью этого инструмента на выходе появится: 1. Регрессионная статистика Позволяет нам оценить качество модели. 2. Дисперсионный анализ Направлен на поиск зависимостей в экспериментальных данных. 3. Графическое представление данных 4. Коэффициенты, стандартная ошибка, t-статистика, верхняя и нижняя границы (df – число степеней свободы, ss – сумма квадратов отклонений, MS= SS/DF) 5. Вывод остатка Остатки = Y*Yпредсказанное
Матричный метод МНК. Понятие статистической процедуры оценивания параметров эконометрической модели. Требования к наилучшей статистической процедуре: несмещённость и минимальные дисперсии оценок параметров.
Оценкой ân параметра a называют всякую функцию результатов наблюдений над случайной величиной X (иначе — статистику), с помощью которой судят о значениях параметра a. Статистические проверки параметров регрессии основаны на непроверяемых предпосылках распределения случайной величины. Они носят лишь предварительный характер. После построения уравнения регрессии проводится проверка наличия у оценок тех свойств, которые предполагались. Связано это с тем, что оценки параметров регрессии должны отвечать определенным критериям: быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции. В отличие от параметра, его оценка ã n — величина случайная. «Наилучшая оценка» ã n должна обладать наименьшим рассеянием относительно оцениваемого параметра a, например, наименьшей величиной математического ожидания квадрата отклонения оценки от оцениваемого параметра М(ã - a)2. Оценка â n параметра a называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т. е. М(ã) = a. В противном случае оценка называется смещенной. Если это равенство не выполняется, то оценка ã, полученная по разным выборкам, будет в среднем либо завышать значение a (если М(ã) > a, либо занижать его (если М(ã) < 0). Таким образом, требование несмещенности гарантирует отсутствие систематических ошибок при оценивании. Оценка â n параметра a называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру:
В случае использования состоятельных оценок оправдывается увеличение объема выборки, так как при этом становятся маловероятными значительные ошибки при оценивании. Поэтому практический смысл имеют только состоятельные оценки. Несмещенная оценка ã n параметра a называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра a, вычисленных по выборкам одного и того же объема n. Так как для несмещенной оценки M(ã n - a)2 есть ее дисперсия Для нахождения оценок параметров (характеристик) генеральной совокупности используется ряд методов. Указанные критерии оценок (несмещенность, состоятельность, эффективность) обязательно учитываются при разных способах оценивания.
Предпосылки применения МНК. (условия Гаусса-Маркова). Всего их 5 1. Математическое ожидание случайного отклонения εi рав- но нулю: M(εi) = 0 для всех наблюдений. Данное условие означает, что случайное отклонение в сред- нем не оказывает влияния на зависимую переменную. В каждом конкретном наблюдении случайный член может быть либо поло- жительным, либо отрицательным, но он не должен иметь система- тического смещения. Отметим, что выполнимость М(εi) = 0 влечет выполнимость M(Y приX=xi) = β0 + β1*xi.
2. Дисперсия случайных отклонений εi постоянна: D(εi) = D(εj) = σ2 для любых наблюдений i и j. Данное условие подразумевает, что, несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть либо большим, либо меньшим, не должно быть некой априор- ной причины, вызывающей большую ошибку (отклонение). Выполнимость данной предпосылки называется гомоскеда стичностью (постоянством дисперсии отклонений). Невыполни- мость данной предпосылки называется гетероскедастичностью (не- постоянством дисперсий отклонений). данную предпосылку можно переписать в форме: М(ε 2i) = σ2.
3. Случайные отклонения εi и εj являются независимыми друг от друга для i ≠ j. Выполнимость данной предпосылки предполагает, что от- сутствует систематическая связь между любыми случайными от- клонениями. Другими словами, величина и определенный знак лю- бого случайного отклонения не должны быть причинами величины и знака любого другого отклонения. 4. Случайное отклонение должно быть независимо от объяс- няющих переменных. Обычно это условие выполняется автоматически, если объ- ясняющие переменные не являются случайными в данной модели. Данное условие предполагает выполнимость следующего со- отношения: cov(εi, xi) = M((εi –M(εi))⋅(xi – M(xi))) = i i = M(εi (xi – M(xi))) = M(εi xi) – M(εi)⋅M(xi) = M(εi x i) = 0. Следует отметить, что выполнимость данной предпосылки не столь критична для эконометрических моделей.
5. Модель является линейной относительно параметров.
Оцененная спецификация Yt= (S T-статистики | Если |
Критическое значение
Проверка качества модели. При оценке качества модели, ее адекватности и точности используются методы математической статистики. В частности, такие приемы как: анализ остаточной последовательности; анализ коэффициентов корреляции; оценка ошибки аппроксимации; оценка значимости коэффициентов регрессии по t–статистике Стьюдента; проверка значимости модели регрессии с использованием F–критерия Фишера и пр. Использование модели Достоинства: • точность; • отсутствие грубых допущений; • возможность учета большого числа факторов; • высокая практическая ценность. Недостатки: • громоздкость; • трудоемкость построения; • невозможность поиска оптимальных решений.
Свойства оценок МНК. Для того чтобы регрессионный анализ, основанный на МНК давал наилучшие результаты, должны выполняться условия Гаусса-Маркова. Если все предпосылки выполняются, то оценки, полученные по МНК, будут обладать свойствами а). несмещённости, б). эффективности, в). состоятельности. А). Несмещённость оценки означает, что матем.ожид. остатков равно нулю. Если оценки обладают свойством несмещённости, то их можно сравнивать по разным исследованиям. Б). Оценки считаются эффективными, если они характеризуются наименьшей дисперсией. В). Состоятельность оценок характеризует увеличение их точности с увеличением объёма выборки.
53. Спецификация и оценивание МНК эконометрических моделей нелинейных по параметрам. (15 баллов). В моделях, нелинейных по параметрам, например, степенных или показательных, непосредственное применение МНК для их оценки невозможно, так как необходимым условием применимости МНК является линейность по коэффициентам уравнения регрессии. В данном случае преобразованием, которое приводит уравнение регрессии к линейному виду, является логарифмирование. После приведения модели к линейному виду, можно применять обычный МНК для оценки её параметров. Пример. Рассмотрим уравнение
т.е. параметр β представляет собой эластичность переменной Y по переменной Х. уравнение не является линейным. Прологарифмируем обе части данного уравнения: ln(Y)=ln(A)+ βln(X)=α+βln(X), гдеα=ln(A). Уравнение линейно относительно логарифмов переменных, поэтому можно применить обычный МНК.
54. Способы корректировки автокорреляции (авторегрессионные модели первого порядка) (15 баллов). Рассмотрим авторегрессионную модель первого порядка, в которой значение возмущения ɛ определяется через его лаговое значение первого порядка. В этом случае спецификация регрессионной модели с регрессией случайного возмущения имеет вид:
где
Необходимо определить начальные условия модели. Начальные условия модели определяются нормальной случайной величиной Корректирующий множитель
55. Способы корректировки гетероскедастичности. Взвешенный метод наименьших квадратов (15 баллов). При наличии гетероскедастичности в остатках рекомендуется традичионный МНК заменить обобщенным методом наименьших квадратов (ОМНК). Этот метод применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии. Будем считать, что среднее значение остаточных величин равно нулю. В то же время дисперсия их не остается неизменной для различных значений фактора, а пропорциональна некоторой величине К. В общем виде уравнение регрессии примет вид По отношению к обычной регрессии уравнение с новыми, преобразованными переменными представляет собой взвешенную регрессию, в которой переменные X и Y взяты с весами Оценка параметров уравнения с преобразованными переменными приводит к взвешенному методу наименьших квадратов, для которых необходимо минимизировать сумму квадратов отклонений:
ОМНК-оценка вектора А равна A= Адаптивные модели прогнозирования. Адаптивные модели прогнозирования – это модели дисконтирования данных, способные быстро приспосабливать свою структуру и параметры к изменению условий. Инструментом прогноза в адаптивных моделях является математическая модель с единственным фактором «время». В основе адаптивных методов лежит модель экспоненциального сглаживания, которая описывается формулой: St = λ yt + (1 - λ) St-1 Где St – значение экспоненциальной средней в момент t; λ – параметр сглаживания, 0 < λ < 1. Когда эта форма применяется рекурсивно, то каждое новое сглаженное значение (которое является также прогнозом) вычисляется как взвешенное среднее текущего наблюдения и сглаженного ряда. Очевидно, что результат сглаживания зависит от параметра λ: · Если λ = 1, то предыдущие наблюдения полностью игнорируются; · Если λ = 0, то игнорируются текущие наблюдения; · Если 0 < λ < 1, то значения λ дают промежуточные результаты. При использовании экспоненциальной средней для краткосрочного прогнозирования предполагается, что модель ряда (модель Брауна) имеет вид: yt = at + εt где at – варьирующий во времени средний уровень ряда; εt – случайные отклонения с нулевым математическим ожиданием и дисперсией σ2.
Прогнозная модель определяется равенством ŷτ(t) = ȃt где ŷτ(t) – прогноз, сделанный в момент t на τ единиц времени вперед; ȃt – оценка at. Единственный параметр модели ȃt определяется экспоненциальной средней ȃt = St, ȃ0 = S0. Начальное значение S0 вычисляется как среднее всех наблюдений. В качестве критерия оптимальности при выборе параметра сглаживания λ обычно принимают критерий минимума ἒ (средней абсолютной величины относительной ошибки)
2. Алгоритм проверки адекватности множественной регрессионной модели (сущность этапов проверки, расчетные формулы, формулировка вывода).
Проверка качества или адекватности множественной модели регрессии состоит из следующих этапов: · Проверка качества уравнения регрессии · Проверка значимости уравнения регрессии · Анализ статистической значимости параметров модели · Проверка выполнения предпосылок МНК Для проверки качества уравнения регрессии вычисляют коэффициент множественной корреляции R и коэффициент детерминации R2.
Чем ближе к единице значение этих характеристик, тем выше качество модели. В многофакторной регрессии добавление дополнительных объясняющих переменных увеличивает коэффициент детерминации. Следовательно, коэффициент детерминации должен быть скорректирован с учетом числа независимых переменных. Скорректированный R2 рассчитывается так:
Где n – число наблюдений, k - число независимых переменных.
Для проверки значимости уравнения регрессии используется F-критерий Фишера, вычисляемый по формуле:
Если расчетное значение с v1 = k и v2 = n – k – 1 степенями свободы, где k – количество факторов, включенных в модель, больше табличного при заданном уровне значимости α, то модель считается значимой.
Анализ статистической значимости параметров модели (коэффициентов регрессии) проводится с использованием t-статистики путем проверки гипотезы о равенстве нулю j-го параметра уравнения (кроме свободного члена):
Где Saj – это стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии аj Величина Saj представляет собой квадратный корень из произведения несмещенной оценки дисперсии S2 и j-того диагонального элемента матрицы, обратной матрице системы нормальных уравнений:
Где bjj – диагональный элемент матрицы (X’X)-1 Если расчетное значение t-критерия с (n-k-1) степенями свободы больше его табличного значения при заданном уровне значимости α, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует исключить из модели (при этом ее качество не ухудшится).
Проверка выполнения предпосылок МНК:
Условия, необходимые для получения несмещенных, состоятельных и эффективных оценок, представляют собой предпосылки МНК: · Математическое ожидание случайной составляющей в любом направлении должно быть равно нулю. · Зависимая переменная yi есть величина случайная, а объясняющая переменная xi – величина неслучайная. Если это условие выполнено, то теоретическая ковариация между независимой переменной и случайным членом равна нулю. · В любых двух наблюдениях отсутствует систематическая связь между значениями случайной составляющей. · Дисперсия случайной величины должна быть постоянна для всех наблюдений
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.68.112 (0.015 с.) |

 и второй регрессии
и второй регрессии 
 . В числителе должна быть бо’льшая сумма квадратов
. В числителе должна быть бо’льшая сумма квадратов




 , то эффективность является решающим свойством, определяющим качество оценки.
, то эффективность является решающим свойством, определяющим качество оценки. +
+ 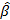 Xt+
Xt+  dt+εt
dt+εt | = |
| = |  |
|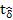 | < t кр, то нулевая гипотеза не отвергается и качественный признак не влияет на модель
| < t кр, то нулевая гипотеза не отвергается и качественный признак не влияет на модель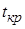 ~ (α, n-k), где α - заданный уровень значимости a, n-k - число степеней свободы из таблиц распределения Стьюдента
~ (α, n-k), где α - заданный уровень значимости a, n-k - число степеней свободы из таблиц распределения Стьюдента ).
). , где А и β – параметры модели. Параметр А степенной модели представляет собой значение эндогенной переменной, полученное при единичном значении регрессора. Для того, чтобы дать экономическую интерпретацию параметру β данной модели, продифференцируем уравнение по переменной Х:
, где А и β – параметры модели. Параметр А степенной модели представляет собой значение эндогенной переменной, полученное при единичном значении регрессора. Для того, чтобы дать экономическую интерпретацию параметру β данной модели, продифференцируем уравнение по переменной Х:

 , t – случайные возмущения авторегрессионного уравнения – независимые нормально распределенные случайные величины:
, t – случайные возмущения авторегрессионного уравнения – независимые нормально распределенные случайные величины: 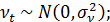
 – коэффициент авторегрессии (параметр модели) (-1<
– коэффициент авторегрессии (параметр модели) (-1< 
 служит для обеспечения гомоскедастичности случайных возмущений.
служит для обеспечения гомоскедастичности случайных возмущений.


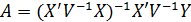 , где
, где , V=
, V=  , X=
, X= 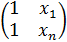 , Y=
, Y=