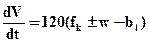Классификация моделей, задачи, решаемые при моделировании. Состав модели.

Моделированием называется изучение свойств объекта путём разработки физической или математической модели этих устройств и исследование этой модели.

При физическом моделировании модель воспроизводит изучаемый процесс или объект с сохранением его физической природы. Математической моделью реальных устройств называется описание их на каком-либо формальном языке, позволяющее исследовать их поведение в определённых ситуациях.

Различают детерминированные и вероятностные (стахостические) модели. Детерминированные модели, представляющие собой совокупность неслучайных соотношений, дают возможность однозначно определить поведения объекта управления (технологического процесса) через его параметры, воздействующие внешние силы и внешние воздействия. Вероятностные модели используются для моделирования таких объектов управления, у которых внутреннее состояние, их характеристики и внешние силы, воздействующие на объекты, носят случайный характер. В этом случае при расчёте модели получаются вероятностные оценки характеристик, которые только с определённой вероятностью отражают их фактическое значение.

В некоторых случаях детерминированную систему целесообразно представить в виде вероятностной. Например, время выполнения программы.

Модель создаётся в зависимости от цели исследования и определяет:

– перечень воспроизводимых характеристик Y= {y₁…y_m}. Состав характеристик Y определяется в зависимости от свойств моделируемого объекта и должен гарантировать полноту отображаемых свойств;

– перечень входных параметров X={x₁…x_N}. В состав вектора параметров X включаются только параметры, существенно влияющие на значения параметров выходных характеристик;

– точность модели – допустимую погрешность воспроизведения выходных параметров при определённых значениях входных величин.

Модели информационных потоков позволяют рассчитать оптимальную сеть передачи данных.

Моделирование управляющей системы в целом используется для определения её надёжности и производительности. Под производительностью понимается точность системы (ошибки выходных параметров, ошибки по скорости или ускорению и т.д.), устойчивость работы в экстремальных условиях и др. Моделирование производительности системы особенно важно в системах реального времени, поскольку позволяет производить корректировку алгоритма работы системы, перераспределение задач между процессорами и др.

Вопрос 6

Аналитические модели.

Аналитические методы исследования объектов управления, технологических процессов и вычислительных систем сводятся к построению математических моделей, которые представляют физические свойства как математические зависимости между выходными и входными параметрами. При использовании аналитических моделей оператор F, устанавливающий зависимость = F () между характеристиками и параметрами объекта, представляется совокупностью математических выражений (формул).

При построении аналитических моделей свойства объекта описываются исходя из свойств составляющих – физических элементов и элементарных процессов. При этом создаются математические выражения, связывающие параметры элементов между собой.

Пример: F=m·a

Уравнение движения поезда:

f_k – удельная сила тяги локомотива

w – удельное сопротивление движению

b_T­ – тормозная сила

Чаще всего аналитическая модель системы представляет собой систему нелинейных дифференциальных уравнений, решение которых, особенно в системах, работающих в режиме реального времени, вызывает большие затруднения. Для упрощения решения уравнений обычно выполняется частично-кусочная аппроксимация зависимостей, вследствие чего при решении модели приходится иметь дело с системой линейных дифференциальных уравнений.

зависимости, полученные аналитическим путём, являются строго доказанными и такие модели не требуют доказательств их адекватности (с учётом указанных выше допущений). Часто аналитические модели используются для доказательства адекватности моделей, построенных с использованием других принципов;

– аналитические модели могу использоваться для изучения свойств объектов (например, поведение объектов в экстремальных ситуациях, определение предельных значений параметров, эффективность влияния изменений входных сигналов и др.);

– аналитические модели вычислительных систем имеют общую познавательную ценность, поскольку позволяют предсказать поведение подобных систем при любых сочетаниях входных параметров.

– При входных сигналах любой формы как правило вычисляют коэфф. Передачи, для исследования переходных процессов используются ступенчатая и еденичная ф-я. При гармонич.вх.сигн.использ. АЧХ, ФЧХ, АФЧХ.

Вопрос 7