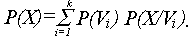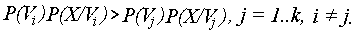Байесовское решающее правило

Недостатком рассмотренных выше методов является то, что они могут применяться только тогда, когда классы чётко разделяются друг от друга. На практике часто встречаются случаи, когда объекты, имеющие совпадающие свойства, относятся к разным классам. Примером могут служить ходовые свойства отцепов. Как правило, тяжёлые отцепы являются хорошими бегунами, а лёгкие – плохими. Но бывает наоборот, тяжёлый бегун оказывается плохим бегуном, а лёгкий – хорошим. Таким образом, объект, имеющий вектор Х свойств, может быть отнесён, с какой-то вероятностью, к любому классу.

Обозначим через P(V_i/X) вероятность того, что объект, имеющий вектор свойств Х, принадлежит классу V_i и через C_ij – потери, вызванные тем, что объект, принадлежащий классу V_i,ошибочно отнесён к классу V_j. Так как объект Х может принадлежать любому из k классов, математическое ожидание потерь, вызванное отнесением этого объекта к классу V_j, будет равно:

Эта величина называется условным средним риском или условными средними потерями.

Вычислим условные средние потери для каждого класса R₁(X), R₂(X), …,R_k(X). Минимальное значение условных средних потерь при отнесении объекта к какому-нибудь классу можно считать признаком того, что объект принадлежит этому классу.

Воспользовавшись формулой Байеса

выражение расчёта условной средней потери можно представить в следующем виде:

Поскольку выражение 1/P(X) входит в качестве множителя во все формулы вычисления условных средних потерь, его можно отбросить.

Для упрощения рассуждений будем считать, что C_ij=0, если i=j (класс определён правильно, потери равны нулю), и C_ij =1, если i ¹ j (потери одинаковы при любой ошибке). Представим функцию потерь в следующем виде: С_ij=1-d_ij,, где d_ij =1, если i = j, и d_ij=0, если i ¹ j.

В этом случае математическое ожидание потерь будет равно:

Поскольку суммирование ведётся по всем классам сумма произведений вероятности класса и вероятности объекта в классе равна вероятности объекта:

Если объект принадлежит классу V_i, должно соблюдаться неравенство:

Отбросив P(X), получим:

Таким образом, решающее правило будет иметь вид:

При этом объект зачисляется в класс V_i, если q_i(x)> q_j(x), j =1..k, j¹ i.

P(Vi)= n_i/n, n – общее число объектов обучающей последовательности, n_i – число объектов обучающей последовательности, принадлежащих классу V_i.

R_i (X)=P(X)P(V_i /X). Как и в предыдущем случае, Р(Х) можно отбросить. Таким образом, основной можно считать решающую функцию:

R_i (X)= P(V_i /X).

В отличие от предыдущей функции её можно использовать даже при сравнительно небольшой выборке объектов обучающей последовательности.

R_i (X)>0,5 – объект принадлежит классу V₁, иначе к V₂.

Вопрос 17

Нахождение коэффициентов решающей функции, построенной с использованием критерия Байеса.

Если число классов равно двум, то R₂(X)=P(V₂/X)=1-P(V₁/X)= 1-R₁(X). В связи с этим достаточно знать только функцию R₁(X) (в дальнейшем её будем обозначать R(X)).

Поскольку классы разделяются гиперплоскостями, решающую функцию будем искать в виде:

где с – вектор коэффициентов решающей функции, с = (с₀,с₁,…,c_k); х – вектор свойств объекта, х = (х₀, х₁,…,х_k); х₀ =1;

Вероятностный алгоритм обучения представляет собой следующую рекуррентную процедуру.

Пусть после просмотра n-1 – го вектора объекта обучающей последовательности получено n –е приближение с (k) коэффициентов решающей функции и рассматривается n –й вектор. Тогда (k+1) –ое приближение коэффициентов определится следующим образом:

 

Процесс вычисления коэффициентов с решающей функции заключается в следующем:

– первоначально коэффициентам с присваиваются произвольные значения, например, с₀=с₁=…=с_k=0;

– поочерёдно в решающую функцию подставляют свойства вектора Х объектов обучающей последовательности и корректируют значения коэффициентов с с использованием указанных выше преобразований.

Для получения более точных значений коэффициентов объекты обучающей последовательности на вход алгоритма подаются многократно. Процедура заканчивается, если разность между одноимёнными коэффициентами двух очередных реализаций алгоритма не превышают значение ошибки e (обычно e =10^-6).

Вопрос 18

Имитационные модели

Имитационное моделирование основано на представлении порядка функционирования системы или отдельного её узла в виде набора алгоритмов. Имитационные математические модели – это алгоритмические модели, отражающие развитие процесса (поведение исследуемого объекта) во времени при заданных внешних воздействий на процесс (объект).

Имитационное моделирование основано на прямом описании моделируемого объекта. Существенной характеристикой таких моделей является структурное подобие объекта и модели. Это значит, что каждому существенному с точки зрения решаемой задачи элементу объекта ставится в соответствие элемент модели. При построении имитационной модели описываются законы функционирования каждого элемента объекта и связи между ними.

Имитационные модели представляют собой описание объекта исследования на некотором языке, которое имитирует элементарные явления, составляющие функционирование исследуемой системы, с сохранением их логической структуры, последовательности протекания во времени, особенностей и состава информации о состоянии процесса. Можно отметить имеющуюся аналогию между исследованием процессов методом имитационного моделирования и экспериментальным их исследованием.

Работа с имитационной моделью заключается в проведении имитационного эксперимента. Процесс, протекающий в модели в ходе эксперимента, подобен процессу в реальном объекте. Поэтому исследование объекта на его имитационной модели сводится к изучению характеристик процесса, протекающего в ходе эксперимента.

Ценным качеством имитационных моделей является возможность управлять масштабом времени, создавать экстремальные ситуации, которые затруднительно или даже невозможно создать при экспериментальном испытании объекта.

При построении имитационных моделей, как привило, используется агрегатный метод, Для этого вся система разбивается на отдельные агрегаты, выполняющие сравнительно небольшой круг задач. Агрегаты могут соответствовать элементам и узлам моделируемого устройства (например, процессор, ОЗУ, устройства обмена информацией и т.д.). В качестве агрегатов могут выступать математические объекты, с помощью которых описывается работа отдельных узлов устройства. По существу агрегат представляет собой описание функций объекта, соответствующих цели исследования.

Агрегаты задаются в параметрической форме, т.е. указываются параметры, характеризующие конкретный объект. Например, система массового обслуживания характеризуется дисциплиной обслуживания заявок, числом каналов и законом распределения длительности обслуживания (указываются параметры закона распределения). Функции агрегата (рис.2.19, а) представляются в алгоритмической форме – в виде процедуры Ф_q(a₁,…a_k, b₁,…b_l, c_l,…c_m), где параметры a₁,…a_k определяют состояние входов элемента, b₁,…b_l – режим его функционирования, и c₁,…c_m – состояние выходов. Таким образом, агрегат представляет собой устройство, преобразующее поток информации, поступающий на его входы А(а₁,…а_n), в выходной поток C(c₁,…c_m) по алгоритму, определяемому состоянием входов B(b₁,…b_m).

Имитационная модель собирается путём соединения выходов одних агрегатов с входами других (рис. 1.19, б). Состав агрегатов, структура связи ними и наборы параметров агрегатов и определяют имитационную модель. Таким образом, имитационные модели воспроизводят процесс функционирования и свойства исследуемых систем исходя из априорно известных свойств элементов системы за счёт объединения моделей элементов в структуру, соответствующую исследуемой системе, и имитации функционирования элементов в их взаимодействии.

 

Важнейшие свойства имитационных моделей:

– с помощью имитационных моделей можно исследовать системы любой степени сложности. Усложнение объекта исследования приводит только к увеличению числа данных, вводимых в модель, усложнению алгоритма их обработки и увеличение времени решения модели. При этом структура модели остаётся неизменной.

– Метод имитации не ограничивает уровень детализации. С помощью алгоритмов можно воспроизводить любые сколь угодно своеобразные взаимосвязи между элементами системы и процессы функционирования. Более детальное представление организации системы сказывается только на объёме алгоритмического описания модели (программы) и затратах времени на моделирование.

– Имитационные модели являются неограниченным источником данных о поведении исследуемой системы, особенно в экстремальных ситуациях. При этом могут быть получены характеристики как системы в целом, так и отдельных её узлов и элементов.

К недостаткам имитационных моделей следует отнести:

– большие затраты времени, необходимые для создания модели и частный характер полученных результатов;

большие затраты времени, необходимые для испытания модели. Опыт создания имитационных моделей сложных систем показывает [9], что для одной реализации модели ЭВМ требуется выполнить 10⁸…10¹² операторов. Поскольку при исследовании модели требуется её многократная прогонка, исследование модели может длиться несколько суток.

Вопрос 19