Объединение, пересечение, взятие разности отношений, прямое или декартовое произведение отношений.

Поскольку отношения (таблицы) являются множествами, средства ма­нипулирования отношениями базируются на традиционных теоретико-множественных операциях, дополненных некоторыми специальными опера­циями, специфическими для баз данных.

Набор основных алгебраических операций состоит из восьми опера­ций, которые делятся на два класса: теоретико-множественные и специаль­ные реляционные операции.

В состав теоретико-множественных операций входят:

- объединение отношений;

- пересечение отношений;

- взятие разности отношений;

- прямое произведение отношений. Специальные реляционные операции включают:

- ограничение отношений;

- проекцию отношений;

- соединение отношений;

- деление отношений.

Кроме того, в состав реляционной алгебры включены: операция при­своения, позволяющая сохранить результаты вычисления алгебраического выражения, и операция переименования атрибутов, дающая возможность сформировать заголовок (схему) результирующего отношения.

Объединение отношений. Объединять отношения можно только в том случае, когда заголовки объединяемых отношений совпадают. Результатом объединения является отношение, имеющее такой же заголовок, что и исход­ные отношения, а тело отношений включает в себя все кортежи, входящие хотя бы один раз в одно из исходных отношений.

ПримерЗ.1. Объединить отношения, представленные в табл. 3.3 и 3,4.

Результирующее отношение получается путём внесения в неё всех кор­тежей, входящих в исходные отношения с последующим исключением кор­тежей-дубликатов (Иванов Й.И. и Козлов К.К. получили по две двойки, но в результирующем отношении их фамилии встречаются только один раз).

Результат объединения отношений представлен в табл. 3.5.

Пересечение отношений. Эта операция также может быть выполнена только в том случае, если заголовки исходных отношений полностью совпа­дают. Результирующее отношение имеет тот же заголовок, а в тело отноше­ния включаются только кортежи, содержащиеся во всех исходных отноше­ниях.

Пример 3.2. Найти пересечение отношений табл.3.3 и 3.4.

Таблица 3.6 Список студентов, получивших неудовлетворительные оценки по обеим дисциплинам

Взятие разности отношений. В данном случае исходные отношения должны иметь совпадающие заголовки, результирующее отношение также будет иметь тот же заголовок. В тело отношения включаются только корте­жи, имеющиеся в уменьшаемом отношении и отсутствующие в вычитаемом отношении. При взятии разности А-В в результирующее отношение будут включены кортежи отношения А, не входящие в отношение В. Разность от­ношений В-А включает кортежи отношения В, не содержащиеся в отноше­нии А.

П ример 3.3. С оставим списки студентов, получивших неудовлетвори­тельные оценки только по математике и только по физике.

Таблица 3.7 Список студентов, получивших неудовлетворительные оценки только по математике

Таблица 3.8 Список студентов, получивших неудовлетворительные оценки только по физике

Прямое (декартово) произведение двух отношений. Эта операция возможна только в том случае, если заголовки отношений не содержат оди­наковых атрибутов. В случае совпадения наименований атрибутов необхо­димо их переименовать. Заголовок нового отношения включает в себя атри­буты обоих отношений, а тело отношения получается путём сцепления (кон­катенации) кортежей исходных отношений. Кардинальное число результи­рующего отношения равно произведению кардинальных чисел исходных от­ношений.

Пример 3.5. П усть Принято решение: студенты, получившие две дойки, могут повторно сдать экзамены за дополнительную плату.

Найдём прямое произведение отношения табл. 3.6 и табл.3.9. Результат представлен в табл. 3.10.

Таблица 3.9 Список экзаменаторов

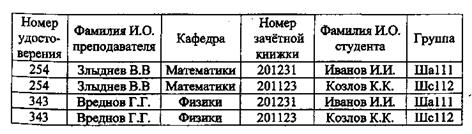
Каждый из исходных отношений имеет атрибут "Фамилия И.О." Вы­полнение операции прямого произведения возможно только после переиме­нования атрибутов.

Таблица 3.10 Ведомость платных переэкзаменовок

Вопрос 35