
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование одноканальной системы массового обслуживания.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим наиболее простой случай применения теории массового обслуживания в моделировании: – поток заявок простейший и определяется интенсивностью их поступления l; – поток обслуживания заявок тоже простейший, интенсивность обслуживания – m. Поскольку потоки поступления заявок и их обслуживания простейшие, за достаточно малое время Dt в систему может поступить только одна заявка и покинуть систему тоже может только одна заявка. За время Dt с вероятностью l×Dt поступит одна заявка и с вероятностью m×Dt очередная заявка будет обслужена. Очевидно с вероятностью 1 -l×Dt ни одна заявка в систему не поступит и с вероятностью 1 -m×Dt ни одна заявка не будет обслужена. Обозначим через Рn (t) вероятность того, что в момент времени t в системе будет ровно n заявок. Рассчитаем вероятность того, что в момент времени t+Dt в системе окажется ровно n заявок. Возможны четыре ситуации, приводящие к этому исходу: – в момент времени t в системе было n -1 заявок, за время Dt поступила одна заявка и ни одна не была обслужена. Вероятность этого события равна: Pn-1(t)×l×Dt×(1-m×Dt); – в момент времени t в системе n заявок, ни одна не поступила и ни одна не обслужена: Pn(t)×(1-l×Dt)×(1-m×Dt); – в момент времени t в системе n заявок, одна поступила и одна обслужена: Pn(t)× l×Dt×m×Dt; – в момент времени t в системе n=1 заявка, ни одна не поступила, одна обслужена: Pn+1(t)×(1-l×Dt)×m×Dt; Вероятность того, что в момент времени t+Dt в системе останется ровно n заявок, равна сумме указанных выше вероятностей: Pn(t+Dt)=Pn-1(t)×l×Dt(1-m×Dt)+ Pn(t)×(1-l×Dt)×(1-m×Dt)+ + Pn(t)× l×Dt×m×Dt+ Pn+1(t)×(1-l×Dt)×m×Dt. Раскроем скобки, исключим слагаемые, в которых содержится Dt в квадрате (величины второй степени малости), перенесём влево Pn(t) и разделим левую и правую части на Dt. Устремив Dt к нулю, получим следующее дифференциальное уравнение:
Это уравнение описывает все возможные ситуации, кроме случаев, когда n= 0. Возможны два независимых случая, когда в момент времени t+Dt в системе нет заявок: – в момент времени t в системе нет заявок, за время Dt они не поступали. Вероятность этого события равна: P0(t)×(1-l×Dt); – в момент времени t в системе одна заявка, она обслужена, другие заявки не поступали: P1(t)×(1-l×Dt)×m×Dt. Следовательно, P0(t+Dt)= P0(t)×(1-l×Dt)+ P1(t)×(1-l×Dt)×m×Dt. Выполнив такие же аналогичные преобразования, получим второе уравнение:
В установившемся режиме вероятности Pn(t) не зависят от времени, поэтому их производные по времени равны нулю. В результате этого получим систему алгебраических уравнений: -P0×l+P1×m=0, n=0, Pn-1×l - Pn(l+m) + Pn+1×m, n>0.
Введём обозначение: r=l¤m. Из первого уравнения получим P1=r×P0. Пусть n= 1, тогда второе уравнение примет вид:
Преобразовав его, получим P2=P0×r 2. Приняв n= 2, получим P3=P0×r 3. Постепенно увеличивая n, получим Pn=P0×r n. Поскольку Определим перечисленные выше характеристики системы: – вероятность занятости канала (доля времени, в течение которого канал занят) – Рож=1-Р0 =r; – вероятность наличия очереди (n> 0) равна Р n>0 = 1 – Р0 – Р1 = r 2; – среднее число заявок, находящихся в системе: nср= =(1-r)r (1 / (1-r))¢ = r /(1-r). Обратите внимание на то, что после выноса r за знак суммы, под знаком суммы оказалась производная от rn; – среднее число заявок, ожидающих обслуживания (длинна очереди), равно nож= nср - 1; – среднее время нахождения заявки в системе (ожидающих в очереди и обслуживаемых) – Tср=nср/m; – среднее время ожидания обслуживания – Тож= Тср-1 / m. Вопрос 11 Модели, построенные с применением Марковских процессов, способы задания систем. Марковская схема с поглощающим состоянием.
Обозначим через l интенсивность входного потока заявок и через m – интенсивность обслуживания заявки одним каналом. Очевидно, система может устойчиво работать, если l < km. При соблюдении этого условия в системе существует стационарный режим, при котором вероятности состояний остаются неименными во времени. Поскольку длина очереди не ограничена, граф состояний системы будет иметь сколько угодно вершин. Максимальная интенсивность обслуживания заявок системой равна km, при числе заявок в системе, большем km, интенсивность обслуживания остаётся неизменной. Граф состояний k– канальной СМО:
Уравнение Колмогорова: Не трудно видеть, что это граф эргодического Марковского процесса. Описывается этот граф системой алгебраических уравнений. n=0: 0 = – p0l + p1m 0 = – pi(l + im) + pi-1l + (i+1)pi+1m, 0 < i < k 0 = – pj(l + km) + pj-1l + k pj+1 m, ¥>j³ k Система решается. Поглощающая Марковская цепь имеет поглощающее состояние, достигнув в которого процесс прекращается. Из какого бы состояния процесс ни начинался, при бесконечно большом числе переходов он окажется в поглощающем состоянии с вероятностью, равной единице. Матрица вероятностей перехода поглощающей Марковской цепи имеет следующий вид:
Граф, моделирующий надёжность дублированной системы с постоянно включенным резервом и обслуживанием. Поскольку отказы устройств и процессы восстановления устройств после отказа подчинены экспоненциальному закону, возле стрелок в место вероятностей указаны интенсивности переходов из одного состояния в другое (l – интенсивность отказа, m – интенсивность восстановления).
Эта Марковская схема отображает функционирование системы до её отказа. При этом в первом состоянии исправны и работают оба блока, во втором – отказал один из блоков, в третьем – отказали оба блока, т.е. отказала система (поглощающее состояние). Над стрелками указаны интенсивности переходов их одного состояния в другое. Для описания работы этого графа используется система уравнений А.Н. Колмогорова. Система уравнений содержит столько уравнений, сколько вершин имеет граф (за исключением поглощающих). Слева записывается производная вероятности нахождения системы в данном состоянии, справа – многочлен, содержащий столько слагаемых, сколько стрелок входит в данное состояние или выходит из него. Если стрелка направлена из данного состояния, соответствующий член имеет знак «минус», в данное состояние – «плюс». Каждое из слагаемых равно произведению интенсивности перехода на вероятность нахождения системы в состоянии, из которого осуществляется переход. В рассматриваемом случае указанный на рис.2.5 граф описывается двумя уравнениями:
Умножим оба уравнения на dt и проинтегрируем их в пределах [0, ¥].
В результате решения этих уравнений получим:
Математическое ожидание времени от момента включения системы до её отказа будет равно: ТСР=Т0+Т1
Вопрос 12
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 525; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.195.180 (0.007 с.) |



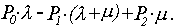
 Pn= 1, получим
Pn= 1, получим 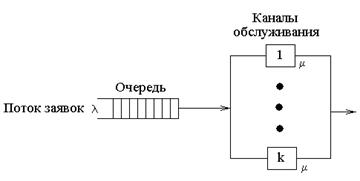


 , где Pi – вероятность нахождения системы в i-том состоянии, справа - S, имеющая столько слаг., сколько имеется переходов из данного сост., и в данное сост., слагаемое является произведением интенсивности перехода на вероятность состояния, из которого осуществляется переход.
, где Pi – вероятность нахождения системы в i-том состоянии, справа - S, имеющая столько слаг., сколько имеется переходов из данного сост., и в данное сост., слагаемое является произведением интенсивности перехода на вероятность состояния, из которого осуществляется переход.
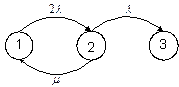



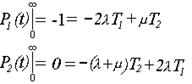
 ТСР=Т0+Т1
ТСР=Т0+Т1



