
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы оценивания линейной модели множественной регрессии в Excel. (15)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1) Надстройка Excel Анализ данных, инструмент Регрессия; 2) Надстройка Excel Поиск решения; 3) Матричные функци Excel по формуле A = 4) По формулам:
41. Модели нестационарных временных рядов с трендом и сезонной составляющей и их идентификация (15 баллов). Большая часть финансовых и экономических временных рядов являются нестационарными, поскольку их вероятностные характеристики, такие, как математическое ожидание, дисперсия, а также автоковариационная и автокорреляционная функции, изменяются с течением времени, т.е. являются функциями времени. При эконометрическом моделировании нестационарных временных рядов различают временные ряды, нестационарные по среднему значению и по дисперсии. Временной ряд является нестационарным по среднему значению, если его математическое ожидание изменяется во времени в соответствии с некоторым детерминированным или вероятностным законом. В данном случае говорят, что временной ряд содержит детерминированный или стохастический тренд. Для описания временных рядов, нестационарных по среднему значению, используются два основных класса моделей: • модели временных рядов с детерминированным трендом, т.е. модели с трендом в виде детерминированной функции времени; • модели интегрированных временных рядов, которые в общем случае представляются в виде модели авторегрессии интегрированного скользящего среднего (autoregressive integrated moving average model - ARIMA model). Дисперсия значений экономических и финансовых переменных может также зависеть от времени, при этом говорят, что соответствующий временной ряд является нестационарным по дисперсии. Эти временные ряды описываются двумя классами моделей: с условной и безусловной неоднородностью (гетероскедастичностью). Эффекты "безусловной" гетероскедастичности часто могут быть смягчены или устранены за счет подходящих функциональных преобразований временного ряда. В задачах финансового анализа особой популярностью пользуются модели типа ARCH с условной гетероскедастичностью.
42. Модели уровней временного ряда: мультипликативная, аддитивная, смешанная (15 баллов). Модели временных рядов – модели, построенные по данным, характеризующим один объект за ряд последовательных моментов времени.
Отдельный уровень временного ряда Y можно представить в виде функции от основных компонент: f (T,S,E), где T - трендовая компонента; S - сезонная (циклическая) компонента; E - случайный шум.
Модель временного ряда может быть представлена в следующих вариантах: 1. Аддитивная модель временного ряда – модель, в которой ряд представлен как сумма тенденции,сезонной, циклической и случайной компонент: Y=T+S+E. 2. Мультипликативная модель временного ряда – модель, в которой ряд представлен как произведение тенденции,сезонной, циклической и случайной компонент: Y=T∙S∙E. 3. Смешанная модель временного ряда: Y=T∙S+E.
Выбор одной из моделей проводится на основе анализа структуры сезонных колебаний. § Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. § Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
Модель временного ряда может быть представлена в следующих вариантах. Аддитивная модель временного ряда:
Мультипликативная модель временного ряда:
Смешанная модель временного ряда:
Модель временного ряда с трендом и аддитивной сезонностью имеет место в том случае, если сезонные колебания не зависят от значений ряда:
Модель временного ряда с трендом и мультипликативной сезонностью имеет место в том случае, если сезонные колебания зависят от значений ряда:
Основная задача эконометрического исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 577; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.148.222 (0.007 с.) |

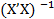 XY;
XY; =
=  ,
, 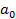 =
= 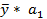 -
- 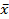
 .
. .
.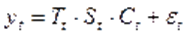 .
. .
.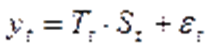 .
.


