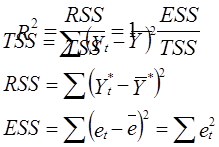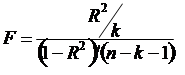Простейшие модели временных рядов.

Модели временных рядов - модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов).

Каждый уровень временного ряда формируется из трендовой (T), сезонной (S), циклической (U) и случайной (E) компонент. (Моделирование циклических колебаний в целом осуществляется аналогично моделированию сезонных колебаний, поэтому далее рассматривается только сезонная компонента S). В зависимости от вида связи между перечисленными компонентами можно построить аддитивную модель временного ряда: Y = T+S+E; или мультипликативную модель: Y = T*S*E. Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний относительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается (непостоянна), строят мультипликативную модель, которая ставит уровни ряда в зависимость от значений сезонной компоненты. Построение моделей сводится к расчету значений T, S и Е для каждого уровня ряда.

Процесс построения модели включает следующие шаги:

1. Выравнивание исходного ряда методом скользящей средней.

2. Расчет значений сезонной компоненты S.

3. Устранение сезонной компоненты из исходных уровней ряда и получение выравненных данных (T + E) в аддитивной или (T*E) в мультипликативной модели.

4. Аналитическое выравнивание уровней (T+E) или (T*E) и расчет значений T с использованием полученного уравнения тренда.

5. Расчет полученных по модели значений (T+S) или (T*S).

6. Расчет абсолютных и/или относительных ошибок.

 

32. F-тест качества спецификации множественной регрессионной модели: выдвигаемая статистическая гипотеза, процедура ее проверки, формулы для расчета статистики (15 баллов).

Под качеством спецификации модели понимается:

- качество выбора функции уравнения регрессии;

- качество выбора набора регрессоров (факторов).

В качестве меры влияния регрессоров на формирование значения эндогенной переменной y вводится коэффициент детерминации R² как отношение регрессионной суммы квадратов к общей сумме квадратов. Коэффициент детерминации показывает, какая доля изменения зависимой переменной обусловлена изменениями объясняющих переменных.

где TSS – общая сумма квадратов эндогенной переменной (Totalsumofsquares)

RSS – регрессионнаясуммаквадратов (Regression sum of squares)

ESS – сумма квадратов остатков (ошибок) (Errorsumofsquares).

Вариация зависимой переменной может быть представлена в виде суммы двух составлящих: TSS = RSS + ESS.

Если R²=1, т.е. RSS=TSS, a ESS=0, то такая модель называется «абсолютно хорошей». Это означает, что выбранные регрессоры полностью объясняют поведение эндогенной переменной.

Если R²=0, т.е. RSS=0, а ESS=TSS, то такую модель называют «абсолютно плохой». В этом случае весь диапазон изменения эндогенной переменной объясняется влиянием случайного возмущения, а выбранные регрессоры не оказывают влияния, не объясняют поведение эндогенной переменной.

Ситуация совершенно плохой спецификации равносильна справедливости статистической гипотезы Н₀: a₁ = a₂ = … = a_k = 0, где a – коэффициенты (параметры) модели. Необходимо помнить, что R² – величина случайная, т.к. его конкретное значение вычисляется по результатам случайной выборки. Это означает, что полученное значение коэффициента детерминации отличное от нуля (R²>0) еще не является достаточным основанием считать модель качественной и опровергнуть гипотезу Н₀.

Замечание. Коэффициент детерминации имеет смысл только при наличии свободного коэффициента a₀ в спецификации.

Для проверки гипотезы H₀ используется F-тест, проверяющий значимость всего уравнения (модели):

1. Формируем случайную величину F_Test с известным законом распределения и вычисляем ее значение:

где: k - количество регрессоров в модели, n – количество наблюдений в выборке. Случайная величина F_Test подчиняется закону распределения вероятностей Фишера.

2. Находим по таблице значение критическое значение F: F_крит (P_дов, k, n-k-1), зависящее от уровня доверительной вероятности и двух параметров: (k) и (n-k-1). В ExcelF_крит можно вычислить с помощью функции FРАСПОБР(вероятность;степени_свободы1;степени_свободы2) или F.ОБР.ПХ, где вероятность – это вероятность, связанная с F-распределением, степени_свободы 1 – это числитель степеней свободы (n₁= k) и степени_свободы 2 – это знаменатель степеней свободы (n₂= (n–k– 1)).

3. Сравниваем значения F_крит и F_Test. Если F_Test ≤ F_кр, то гипотеза H₀: a₁ = a₂ = … = a_k = 0 принимается, значит, качество регрессии неудовлетворительно и у регрессоров отсутствует какая-либо объясняющая способность в рамках линейной модели. Напротив, когда F_Test> F_кр, гипотеза H₀ отклоняется и качество регрессии удовлетворительно, т.е. выбранные регрессоры (но не обязательно все из них!!! еще необходимо каждый из них по t-критерию проверить!) объясняют поведение эндогенной переменной y.