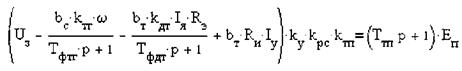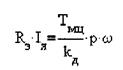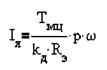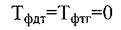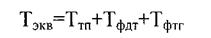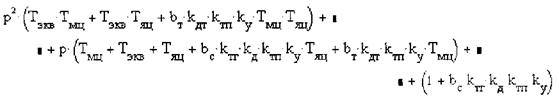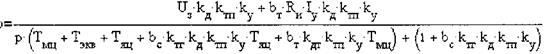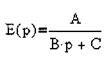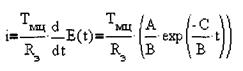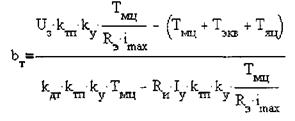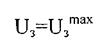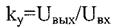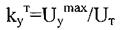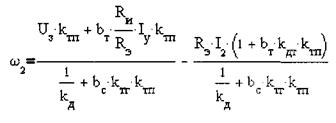Определение максимального напряжения задатчика скорости

Напряжение задания, соответствующее верхнему уровню ско­рости, находим из (2.5) без нагрузки с одной обратной связью по скорости [10].

Для нахождения напряжения задания перепишем (2.5) в не­сколько ином виде

(2.16)

 

где w ₀ - скорость идеального холостого хода двигателя, рад/с.

Скорость идеального холостого хода на верхней и нижней границах регулирования находим из выражения

(2.17)

 

(2.18)

(2.19)

При k_pc=l и k_y=l получаем

Выражаем из этого выражения максимальное напряжение за­дания U₃^max, учитывая, что I_я=Iном- представляет собой номинальный ток двигателя

(2.20)

 

где w ₀ - скорость холостого хода, соответствующая верхнему уров­ню регулирования скорости.

2.4. Определение коэффициента обратной связи по току [10]

Требуется в соответствии со структурной схемой (рис.2.2) найти коэффициент обратной связи по току.

Составим систему уравнений, полностью описывающих сис­тему «тиристорный преобразователь - двигатель постоянного тока», на основе структурной схемы (рис.2.2) [3,4]:

- уравнение связи входа и выхода тиристорного управляемого выпрямителя

(2.21)

 

- уравнение связи выхода преобразователя и электрической части электродвигателя (якорной цепи системы «преобразователь-двигатель»)

(2.22)

 

— уравнение связи входа и выхода механической части элек­тродвигателя

(2.23)

 

 

Здесь переменные (см.п.2.2):

I_Я - ток якорной цепи двигателя, А;

I_У - ток уставки (отсечки) двигателя, А;

I_С - ток статической нагрузки двигателя, А;

R_и - сопротивление измерительного резистора, Ом;

b_т - коэффициент рассчитываемой обратной связи по току;

Тфтг - постоянная времени фильтра датчика скорости, с;

Тфдт - постоянная времени фильтра датчика тока, с;

Т_тп - постоянная времени тиристорного преобразователя, с;

Т_яц - электромагнитная постоянная времени главной цепи объекта управления, с;

Т_мц - электромеханическая постоянная времени главной цепи объек­та управления, с;

р - оператор Лапласа.

Все переменные типовых звеньев, которыми представлена рассматриваемая система электропривода, как элементы динамиче­ской системы подробнее будут рассмотрены в разделе 3.

Исследование работы электропривода производится отдельно по управляющему воздействию при М_с=0 (эквивалентно I_C*R_Э=0) и по возмущающему воздействию при U₃=0 или U₃=const. Поэтому уравнение (2.23) необходимо переписать в виде

(2.24)

 

Настройку системы управления электроприводом производим при k_pc=l, вследствие последующего введения корректирующих це­пей.

Преобразуем уравнения (2.22) и (2.23) этой системы к более удобному виду

(2.25)

(2.26)

 

Подставляя (2.26) в (2.21) и (2.25), получаем систему

 

(2.27)

 

(2.28)

 

Преобразуя систему и подставляя (2.28) уравнение в (2.27), получаем

(2.29)

 

Выражаем угловую скорость вращения электродвигателя

(2.30)

 

(2.31)

 

Рассмотрим отдельно знаменатель этого уравнения

(2.32)

 

 

Учитывая, что запаздывание в цепи обратной связи, обуслов­ленное фильтрами на выходе датчиков, обычно невелико и характер изменения самой выходной величины примерно идентичен характе­ру изменения выходного напряжения датчика, можно в передаточ­ной функции фильтров положить, что

(2.33)

 

и, кроме того,

 

(2.34)

где

 

(2.35)

 

Здесь расчет постоянных времени рассмотрен в разделе 3 «Расчет динамики электропривода».

Поэтому (2.32) принимает вид

(2.36)

 

(2.37)

Раскрываем скобки и группируем по степеням

 

(2.38)

Пренебрегая высшими степенями и подставляя знаменатель в (2.31) получаем

 

Выразим ЭДС электродвигателя (см.рис.2.2)

Рис.2.4. Звено конструктивного коэффициента электродвигателя.

(2.39)

 

Учитывая (2.39) из (2.38) получаем выражение для ЭДС элек­тродвигателя

(2.40)

 

Коэффициент усиления обратной связи по току b_т находиться из условия ограничения тока в начальный период переходного про­цесса. Для этой цели понижаем порядок операторного уравнения (2.37) за счет пренебрежения малыми постоянными времени.

Зависимость ЭДС двигателя от времени можно получить ре­шением операторного уравнения (2.40).

Вводим обозначения

(2.41)

Получим

(2.42)

 

Для получения зависимости ЭДС двигателя от времени дом-ножим (2.40) на 1/р

(2.43)

 

Решая это уравнение, получаем зависимость ЭДС электродви­гателя во времени

 

(2.44)

 

Исходя из структурной схемы (рис.2.2), динамический ток [10]

(2.45)

 

Максимальный ток будет иметь место при t=0. Следовательно

(2.46)

 

Так как при t, близком к нулю, E(t)=0, будем считать, что об­ратная связь по скорости еще не действует (b_с=0) - вследствие дей­ствия инерции двигатель еще не разогнался. При этих условиях уравнение (2.46) можно записать

(2.47)

 

Разность между максимальным током I_max и током уставки I_У должна быть меньше 0.2*I_max. Т.е. 0.8*I_max<I_y<I_max. Значение I_max бе­рется не более допустимого по условиям коммутации в двигателе. Для электродвигателей постоянного тока значение предельно допус­тимого тока лежит в пределах I_mах=(2..З)*Iном

Из (2.47) получим

(2.48)

 

 

При k_y=l получаем

(2.49)

Учитывая, что

 

 

будет

и сопротивление измерительного резистора для узла отсечки

R_и=R’_и= R_И /R_Э

перепишем (2.49) в виде

(2.50)

 

2.5. Определение коэффициентов усиления суммирующего усилителя

Требуется найти коэффициенты усиления суммирующего уси­лителя по каналам задающего воздействия, напряжений обратной связи по скорости и току.

Коэффициент усиления суммирующего усилителя па каждому из каналов находится по однотипной формуле [13]

 

Для канала по задающему воздействию коэффициент усиления суммирующего усилителя находиться

 

Для канала обратной связи по скорости коэффициент усиления суммирующего усилителя можно найти

 

(2.53)

где из условия работы двигателя на максимальной требуемой угло­вой скорости вращения

(2.54)

 

 

Для канала обратной связи по току коэффициент усиления суммирующего усилителя будет

 

 

(2.55)

где из условия протекания в якорной цепи двигателя при его работе на рассчитываемую нагрузку тока равного I_ПОТ

(2.56)

 

Для удобства построения статической характеристики следует внести все найденные значения в табл.2.1.

2.6. Построение статической характеристики электропри­вода в замкнутой и разомкнутой системе управления [14]

К системам автоматического управления электроприводами предъявляется и целый ряд требований, обусловленных в каждом конкретном случае спецификой технологического процесса и режи­мом работы производственной машины. Среди них важнейшее ме­сто занимают требования обеспечения заданных статических и ди­намических характеристик электропривода. Эти требования в значи­тельной мере определяют выбор структуры автоматической системы управления электроприводом и ее параметров, что составляет одну из главных задач проектирования автоматизированных электропри­водов.

Статическая характеристика замкнутой системы преобразова­тель-двигатель представляет собой графическое изображение зави­симости регулируемой переменной системы от основного возму­щающего воздействия f1 в установившемся режиме при фиксиро­ванном значении задающего воздействия g и отсутствии других воз-

 

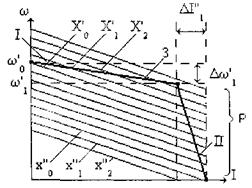
мущающих воздействий f1, f2,... Влияние последних сказывается в виде «дрейфа» статической характеристики или приводит к искаже­нию ее формы. Статическая характеристика может иметь несколько участков разной формы, каждый из которых соответствует опреде­ленным структурам или параметрам системы, если они фиксировано изменяются в процессе управления.

На рис.2.5 показана статическая электромеханическая харак­теристика 3, типичная для многих замкнутых систем преобразова­тель-двигатель постоянного тока. Она представляет собой зависи­мость скорости двигателя со от протекающего в его якорной цепи то­ка I при использовании различных регулирующих обратных связей. На этом же рисунке изображено семейство Р статических электро­механических характеристик разомкнутой системы преобразователь-двигатель. Каждая из этих характеристик отвечает фиксированному значению xi управляющего сигнала x.

Рис.2.5. Статическая электромеханическая характеристика системы.

Характеристика 3 состоит из двух участков. На участке 1 дей­ствуют обратные связи, стабилизирующие скорость двигателя. По­этому здесь регулируемая величина у^'=w’, а момент двигателя мож­но рассматривать как основное возмущающее воздействие, посколь­ку в установившемся режиме M'=M'_c=f1 Когда М'=0 скорость име­ет значение Y'₀=w’₀, а управляющий сигнал х’=Х'0. При увеличении момента нагрузки под влиянием обратных связей происходит непре­рывный переход с одной механической характеристики разомкнутой системы на другую вследствие возрастания управляющего сигнала (характеристики Р при X'1, Х'2, Х'3....). Поэтому характеристика 3, представляющая собой совокупность точек семейства Р, становиться на участке I значительно жестче характеристик разомкнутой систе­мы. Перепад скорости на этом участке Dw’₁=w’₀ - w’₁ (т.е. DY’₁= Y’₀ - Y’₁) при изменении момента от М'=0 (f'₁=0) до M'=M'₁ (f'₁=F'₁₍₁₎)) характеризует стабильность регулирования, т.е. точность поддержа­ния постоянства скорости при наличии возмущающего воздействия f'₁₌M’_c

При переходе к участку II характеристики 3 стабилизирующие скорость обратные связи отключаются и вводиться в действие отри­цательная обратная связь по току, т.е. изменяется структура систе­мы. Последняя теперь будет работать в режиме —автоматического регулирования момента двигателя, т.е. здесь у''=I''. При этом ско­рость двигателя представляет собой основное возмущающее воздей­ствие (в установившемся режиме w"=w"_с=f''₁). При неподвижном двигателе Y''0=I''0=I''кз и управляющий сигнал х"=Х''0). С увели­чением скорости, благодаря действию регулирующей обратной свя­зи по току растет сигнал х" принимая последовательные значения Х"₁, Х"₂, Х''₃..., что отвечает переходу изображающей точки ха­рактеристики 3 по соответствующим характеристикам семейства Р. Поэтому на участке II замкнутой системы значительные изменения скорости сопровождаются относительно небольшими изменениями

тока. Перепад тока DI’’₁= I’’₀ - I’’₁ (т.е. DY’’₁=Y’’₀ - Y’’₁) определяет здесь точность поддержания постоянства тока при изменении воз­мущающего воздействия от w’’=0 (f’’₁ =0) до w’’=w"₁(f’’=F'’₁₍₁₎). Участок II предусматривается, например, для ограничения тока дви­гателя в процессе его пуска, для защиты технологической машины от перегрузки и т.д.

Введение в замкнутые контуры элементов с нелинейными ха­рактеристиками вида:

- задержанная обратная связь по току - отсечка;

- ограничение амплитуды напряжения управления и т.д.

позволяют создать специальные статические характеристики, например экскаваторную (упорную). Подобными нелинейными эле­ментами оснащены все современные системы автоматического управления электроприводами.

Построим статическую характеристику для системы электро­привода изображенной на рис.2.2.

В соответствии с рис.2.2 и при учете всех обратных связей из (2.3) можно записать уравнение

(2.57)

Для данной схемы электропривода, статическая характеристи­ка имеет вид экскаваторной (рис.2.6) с тремя участками [1].

На первом участке (I) при токе от 0 до тока отсечки I_У действу­ет только обратная связь по скорости U_oc (если есть, то по напряже-

 

нию и положительная по току). На втором участке (II) включается в действие отрицательная обратная связь по току U_T от I_У до I₂, и дей­ствуют все обратные связи. На третьем участке (III) отключаются связи по скорости (если есть, то по напряжению и положительная по току), а действует только постоянное напряжение задания по току Uvd=const и отрицательная связь по току до скорости w=0, где ток равен предельно допустимому I_уп=Imах.

 

Рис.2.6. Статическая характеристика электропривода.

Действие одной отрицательной обратной связи по скорости на первом участке (рис.2.6) характеризуется двумя точками: точкой хо­лостого хода w₀ и точкой (1) вступления в действие отрицательной связи по току с отсечкой. На этом участке скорость определяется выражением

(2.58)

 

При построении первой части статической характеристики не­обходимо найти точку холостого хода электропривода с координа­тами (I_Я=0; w₀), воспользовавшись (2.17) и (2.18), где w₀ соответству­ет w_0max, и точку (1) с координатами (I_У; w₁), воспользовавшись уравнением

(2.59)

либо построить первый отрезок статической характеристики по

формулам

(2.60)

Где

Второй участок характеризуется вступлением в действие от­рицательной обратной связи по току, которая увеличивает наклон (уменьшает жесткость) механической характеристики. Задаваясь то­ком I₂ большим чем I_у, можно найти вторую точку (2) характеристи­ки на этом участке. Ее координаты (I₂; w₂), где из (2.3)

(2.61)

 

где

по формуле

Можно построить второй участок статической характеристики

 

(2.62)

Дальнейшая работа электропривода происходит следующим образом: увеличение сигнала управления с ростом нагрузки приво­дит к пробою стабилитрона в узле отсечки, после чего в системе управления начинает действовать фактически только одна отрица­тельная связь по току с постоянным напряжением управления, рав­ным напряжению пробоя стабилитрона Uvd⁼const, а уравнение элек­тромеханической характеристики на третьем участке имеет вид

(2.63)

 

Принимая w_з=0 и I _з=I_max, можно найти U vd.

Третий участок статической характеристики строиться по

формуле

(2.64)

где

Построим статическую характеристику разомкнутой системы в соответствии с (2.4) при отсутствии обратной связи по скорости

(2.65)

 

Напряжение задания в этом случае находится из условия

w=w_{н о м} , I_я=0

Изменение коэффициентов передачи по скорости (если есть, то по напряжению и положительной по току) приведет к изменению угла наклона статических характеристик на первом и втором участ­ках. Наклон статической характеристики на третьем участке зависит только от коэффициента передачи задержанной отрицательной об­ратной связи по току.

Отрицательная обратная связь по напряжению действует так же, как и отрицательная связь по скорости, она компенсирует паде­ние напряжения в цепи преобразователя под воздействием нагрузки, но не компенсирует падение напряжения в якоре двигателя. Поэтому при изменении коэффициента усиления отрицательной обратной связи по напряжению до максимального значения статическая ха­рактеристика может приблизиться к естественной характеристике двигателя. С одной отрицательной связью по напряжению невоз­можно получить режим, когда заданный перепад скорости меньше перепада скорости на естественной характеристике двигателя.

Комбинации различных обратных связей обеспечивают полу­чение различных статических характеристик замкнутых систем управления электроприводом постоянного тока.

 

2.7. ВЫВОДЫ ПО РАЗДЕЛУ

В данном разделе были определены коэффициенты обратных связей по скорости и току, максимальное напряжение задания задат-чика скорости, коэффициенты промежуточного усилителя по кана­лам задающего воздействия и обратных связей, а так же построены статические электромеханические характеристики электропривода в замкнутой и разомкнутой системе управления.