
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряженное состояние в точкеСодержание книги
Поиск на нашем сайте
Напряженное состояние в точке можно описать с компонентами напряжения: δх, δу, δz, τху, τxz, τyz,
δх, δу, δz. - нормальные напряжения τху,τxz,τyz - касательные напряжения z δz
τхz
τzy τxz
τxy δх δх τyz х
y δу
Обобщенный закон Гука Согласно закону Гука деформация прямо пропорциональна нормальному напряжению:
где
Е – модуль Юнга (модуль деформации при растяжении и сжатии). μ - коэффициент Пуассона, характеризует упругие свойства тела, связывает деформации по взаимно перпендикулярным направлениям. γ - деформации сдвига.
где G – модуль деформации при сдвиге, причем:
Действие внешних сил приводит к изменению не только линейных размеров и форм тела, но и объема. Объемная деформация пропорциональна среднему напряжению:
где ΔV – изменение объема элементарного куба под действием внешней нагрузки; V – начальный объем элементарного куба; К – модуль объемной деформации.
Тогда, обобщенный закон Гука записывается в виде:
Зависимость напряжения от деформации для различных тел:
δс – предел прочности хрупкого тела, δs', δs" - пределы текучести Соответственно, зависимости δ от деформации έ различают: 1- хрупкие тела, 2- упрочняющиеся тела, 3- идеально упруго-пластические тела.
Хрупкие (1) деформируются упруго вплоть до разрушения. Упрочняющиеся (2) тела до предела текучести деформируются упруго, а после происходит пластическая деформация. Идеально упруго-пластические (3) до предела текучести также упруго деформируются, затем пластическая деформация увеличивается при постоянном напряжении. Основными видами разрушений является отрыв и срез. Отрыв характерен для хрупких тел, пластические деформации незначительны, поверхность разрушения перпендикулярна к напряжению. Для пластических и упрочняющихся тел характерно разрушение срезом, поверхность разрушения совпадает с плоскостью действия макс. касательных напряжений. 3.3. Условия перехода твердых тел из упругого состояния в пластическое. Условие Треска-Сен-Венана (Треск – француз. инженер):
Пластическое состояние наступает, когда во всех точках среды макс. касательное напряжение достигает определенного значения: 2 | τ2 | = |σ1-σ3| =σs, (3.8) где σs – предел текучести материала при простом растяжении.
Условие Мизеса определяет пластическое состояние в случае, когда удельная упругая энергия изменения формы достигает определенной величины, характерной для материала данного тела Удельная упругая энергия деформирования:
U можно представить в виде суммы удельных энергий упругого изменения объема U0 и упругого изменения формы Uф. Удельная упругая энергия изменения объема:
Тогда удельная упругая энергия изменения формы: Uф=U-U0 = ½ (σ1ε1 + σ2ε2 + σ3ε3) – 3 (1-2μ) σ02/2Е (3.11) После преобразований получим:
Условие Мизеса учитывает 3 главных напряжения и в случае 3-осного напряженного состояния дает лучшие результаты, чем условие Треска-Сан-Венана, которое не учитывает σ2. Теории прочности. Первые исследования, проводимые Леонардо да Винчи и Галилеем привели к созданию первой теории прочности, согласно которой предельное состояние наступает тогда, когда достигает предельного значения одно из главных напряжений: -σn < σ1 < σn; -σn < σ2< σn; (3.13) -σn < σ3 < σn, где σn – предельное напряжение, полученное при одноосном растяжении (+) или сжатии (-).
Вторая теория прочности определяет предельное состояние в случае, когда главная деформация достигает предельного значения. Запишем через обобщенный закон Гука, используя нормальные напряжения: -σn < σ1 - μ (σ2 + σ3) < σn; -σn < σ2- μ (σ1 + σ3) < σn; (3.14) -σn < σ3 - μ (σ1 + σ2) < σn.
Третья теория прочности При разрушении или достижении пластического состояния значительную роль играют касательные напряжения. Условие прочности имеет вид: -τn < τ1 < τn; -τn < τ2 < τn; (3.15) -τn < τ3 < τn; Выразим касательные напряжения через нормальные:
получим: -σn < σ2 - σ3 < σn; -σn < σ1 - σ3 < σn; - третья теория прочности (3.17) -σn < σ1 - σ2 < σn.
Третья теория прочности совпадает с условиями Треска-Сен-Венана. С экспериментальными данными хорошо согласуется при двухосном напряженном состоянии, нашла применение в технике.
Четвертая или энергетическая теория прочности связывает разрушение или достижение пластического состояния с предельным значением удельной энергии формоизменения. Запишем это условие через главные нормальные напряжения: 2σ2n ≥ (σ1 – σ2)2 + (σ1 - σ3 2 +(σ2 - σ3)2 (3.18) Проведем аналогию с условиями Мизеса.
По теории прочности Uфп ≥ Uф. Произведя соответствующие преобразования, можно убедиться, что энергетическая теория прочности совпадает с условием Мизеса. Энергетическая теория носит название Губера-Мизеса-Генки.
Теория прочности Мора определяет зависимость предельного напряжения от среднего напряжения. τn=f(σср), - теория прочности мора, где (3.21) τn- предельное значение касательных напряжений.
Графически выражением теории прочности Мора является огибающая кругов Мора, построенная по результатам испытаний.
σр – предел прочности при растяжении Недостатком этой теории является то, что не учитывается главное напряжение - σ2 Обобщенное условие прочности Мора в отличии от теории прочности Мора учитывает все главные напряжения σin=f(σ0), где σin – предельная интенсивность касательных напряжений, определяемая по формуле:
где σ0 – среднее напряжение. σ0 = 1/3 (σ1+ σ2+ σ3)(3.24) Реологические модели Реология изучает поведение деформируемых тел во времени. Для реальных твердых тел закон Гука выполняется лишь приближенно. 1) Реологическое уравнение твердовязкого тела (тела Кельвина-Фохта). Характерным является наличие зависимости деформации от времени, т.е. проявление вязкостных свойств твердых тел. Например: в случае быстрой погрузки модуль деформации при погружении несколько меньше, чем при разгрузке, что влечет за собой остаточную деформацию εост. а)
Это явление носит название упругого гистерезиса (а). Но с течением времени исчезает остаточная деформация и твердое тело восстанавливает свои размеры. Это явление называют упругим последствием. При наличии этих явлений реологическую модель твердого тела представляют как комбинацию идеально упругого и вязкого тел. Для вязкого тела справедлив закон внутреннего трения Ньютона:
где η – коэффициент вязкости; t – время; γ – деформация. При параллельном деформировании двух тел получается выражение:
Решение этого уравнения, при приложенном напряжении τ0 в момент времени t=0 имеет вид:
2) Реологическое уравнение упруговязкого тела Максвелла. Рассматривается случай, когда происходит релаксация напряжений и ползучесть одновременно. Релаксация напряжений характеризуется самопроизвольным уменьшением напряжений для тела, которое деформировано и в напряженном состоянии находится в течение длительного времени. Ползучестью называется постепенное увеличение деформации при длительном действии на твердое тело нагрузки.
A’B’ – неустановившаяся ползучесть; B’C’ – установившаяся ползучесть; C’D’ – разрушение. Деформация тела представляется как сумма упругой γу и вязкой γв деформаций, которые удовлетворяют условиям:
Скорость деформирования при этом
Решение уравнения с учетом Gγ0=τ0, если к моменту времени t=0 тело деформировано на величину γ0 и даже деформация во времени не изменяется
Для случая, когда тело не деформировано к моменту времени t=0, а затем приложено постоянное напряжение τ0, то общая деформация:
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.213.129 (0.007 с.) |























 τyz
τyz (3.1)
(3.1) - деформация растяжения или сжатия;
- деформация растяжения или сжатия;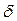 - нормальное напряжение;
- нормальное напряжение; , (3.2)
, (3.2) (3.3)
(3.3) (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6) (3.7)
(3.7)
 (3.9)
(3.9)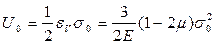 (3.10)
(3.10) - УСЛОВИЕ МИЗЕСА (3.12)
- УСЛОВИЕ МИЗЕСА (3.12) ;
; 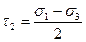 ;
;  (3.16)
(3.16)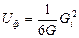 (3.19)
(3.19)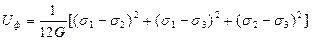 , (3.20)
, (3.20) ;
; 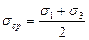 (3.22)
(3.22)
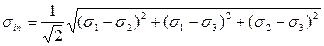 , (3.23)
, (3.23) б)
б) 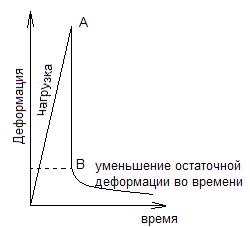
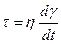 ; (3.25)
; (3.25)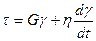 - реологическое уравнение твердовязкого тела (тела Кельвина-Фохта).
- реологическое уравнение твердовязкого тела (тела Кельвина-Фохта).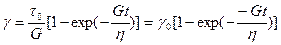 (3.26)
(3.26)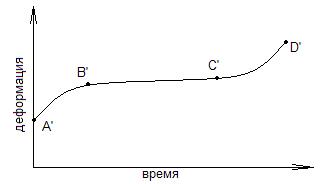
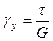 ;
; 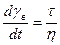 . (3.27)
. (3.27) - упруговязкое тело Максвелла. (3.28)
- упруговязкое тело Максвелла. (3.28)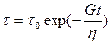 - называется уравнением релаксации напряжений. (3.30)
- называется уравнением релаксации напряжений. (3.30) - уравнение установившейся ползучести. (3.31)
- уравнение установившейся ползучести. (3.31)


