
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основная формула в расчетах на прочность при изгибе. Форма эпюр нормальных и касательных напряженийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте формула: σ= ЕУ
Осевые и полярные моменты сопротивления Осевыми моментами сопротивления относительно осей y и z называются величины:
Полярными моментами сопротивления называется величина:
Моменты сопротивления прямоугольного поперечного сечения
Моменты сопротивления кругового сечения
Момент сопротивления кольцевого сечения
Нормальные напряжения при поперечном изгибе Основные гипотезы: 1) Поперечное сечение бруса, плоские до деформации остаются плоскими и перпендикулярными к оси бруса после деформации (гипотеза Бернулли) 2) Продольные волокна бруса не давят друг на друга
При поперечном изгибе поперечные сечения искажаются под действием поперечной силы, а продольные волокна давят друг на друга, но это не оказывает заметного влияния на величину и характер распределения нормальных напряжений. Поэтому при поперечном изгибе нормальные напряжения определяются по тем же формулам, что и при чистом изгибе
Максимальные напряжения (σ max)
При поперечном изгибе нормальные напряжения изменяются по длине балки пропорционально изгибающему моменту
Касательные напряжения при изгибе. Формула Журавского
Iz – момент инерции; b(y) – ширина сечения, на уровне которого вычисляется напряжение.
Распределение касательных напряжений по высоте различных сечений
Главные напряжения при изгибе Для плоского напряженного состояния главные напряжения вычисляются по формуле:
Положение площадок, по которым действуют главные напряжения вычисляются по формуле:
Т.к. напряжения τ и σ пропорциональны M и Q, то максимальные главные напряжения возникают в сечениях, где М и Q одновременно имеют максимальные значения
Расчет на прочность при изгибе Подавляющим в большинстве случаев нормальные напряжения больше касательных, поэтому основная проверка на прочность – проверка по нормальным напряжениям. 1) Проверка прочности
Если материал не одинаково сопротивляется растяжению (сжатию) то, проверку прочности следует производить отдельно для каждой зоны
2) Подбор сечения
3) Определение нагрузки
Если в балке пролет незначителен, то следует провести дополнительную проверку по касательным и главным напряжениям.
4) Проверка прочности по касательным напряжениям
5) Проверка прочности по главным напряжениям
Проверка по главным напряжениям делается в сечении, где Qy и Mz имеют одинаково большие значения
Дифференциальное уравнение упругой линии Перемещение центра тяжести сечения в направлении перпендикулярном оси балки называется прогибом и обозначается υmax Изогнутая ось балки – это стрела прогиба, называется упругой линией Углом поворота сечения (θ) называется угол на который поворачивается сечение относительно первоначального положения
Система координат принимается следующая: начало координат находится в крайнем левом сечении, ось иксов направлена вдоль оси стержня, ось у перпендикулярна ей. Прогиб балки положителен, если перемещение происходит вверх вдоль оси стержня.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1299; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

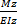 =
=  - опредедляет напряжения в любой точке сечения. Из этой формулы следует: 1. Норм.напряж. max в точках наиб. Удаленных от нейтр.линии при y=ymax. 2. Норм.напр.=0 на нейтр.л. при у=0. 3. Норм. Напр. Одинаковы в точках равноудаленных от нейтральной линии. Обозначим σ=
- опредедляет напряжения в любой точке сечения. Из этой формулы следует: 1. Норм.напряж. max в точках наиб. Удаленных от нейтр.линии при y=ymax. 2. Норм.напр.=0 на нейтр.л. при у=0. 3. Норм. Напр. Одинаковы в точках равноудаленных от нейтральной линии. Обозначим σ=  , Wz - момент сопротивления, а эта формула определения напряжений в наиб.удаленных точках от н.л. Это основная формула в расчетах на прочность
, Wz - момент сопротивления, а эта формула определения напряжений в наиб.удаленных точках от н.л. Это основная формула в расчетах на прочность
 , ymax, zmax – расстояние от осей до наиболее удаленных точек сечения
, ymax, zmax – расстояние от осей до наиболее удаленных точек сечения , Ρmax – расстояние от полюса до наиболее удаленных точек сечения
, Ρmax – расстояние от полюса до наиболее удаленных точек сечения

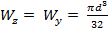 , а полярный момент инерций равен Wp=
, а полярный момент инерций равен Wp=  =
= 

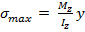

 Qy –поперечная сила, Sz – статический момент полусечения относительно Oz
Qy –поперечная сила, Sz – статический момент полусечения относительно Oz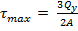 A = hb прямоугольное
A = hb прямоугольное
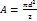 круговое
круговое A = AD-Ad кольцевое
A = AD-Ad кольцевое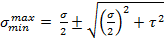

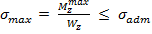 основная формула при расчете на прочность при изгибе
основная формула при расчете на прочность при изгибе при растяжении
при растяжении при сжатии
при сжатии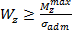 зная момент сопротивления и форму поперечного сечения можно определить его размеры
зная момент сопротивления и форму поперечного сечения можно определить его размеры


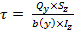

 основное дифференциальное уравнение упругой линии при малых перемещениях
основное дифференциальное уравнение упругой линии при малых перемещениях


