
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет балки на прочность по нормальным сечениямСодержание книги
Поиск на нашем сайте
Высоту сечения балки определяем по МВ =-104,67 кН∙м, принимая ширину ребра ее b =220 мм и задаваясь значением x=0,35.
Тогда h=h0+a =440,3+40=480,3 мм. Принимаем h =500 мм. Отношение h/b =500/220=2,27 лежит в допустимых пределах (1.5…2,5), а высота соответствует предварительно принятой, поэтому пересчета нагрузок не требуется. Расчет арматуры (рис. 4 и 8) а) Крайний пролет. M1 =133,21 кН∙м; h =500 мм; сечение тавровое (полка находится в сжатой части). Предварительно принимаем а =57 мм; h0 = h-a =500-57=443 мм.
Расчетная ширина полки:
Принимаем в расчете
x = ξ·h0 =0,041∙443=18,2 мм
По таблице приложения А принимаем арматуру: 2Æ18 А400 +2Æ16 А400 с Аs =509+402=911 мм2 (+3,2%). Тогда а =(509*35+402*85)/911=57,06 мм - соответствует предварительно принятому значению и перерасчет арматуры не требуется. б) Вторая с края опора В. МВ =-104,67 кН∙м; h =500 мм; сечение прямоугольное, шириной b =220 мм (полка в растянутой зоне – рис.8, б) а =35 мм; h0=h-а =500-35=465 мм.
Принято: 4Æ16 А400 с Аs =804 мм2(+4,9%). в) Средние пролеты. На положительный момент М2=91,58 кН∙м. h =500 мм; сечение тавровое (полка на стороне сжатой части сечения – рис. 8, а); а =60 мм; h0 =440 мм. Расчетная ширина полки:
Принимаем в расчете
x=ξ∙h0 =0,029∙435=12,4 мм т. е. нейтральная ось действительно находится в полке.
Принято 4Æ14А400 с Аs =616 мм2(+2,1%). а =35+50/2=60мм. Пересчет арматуры не требуется. На отрицательный момент М6-7 =-37,37 кН∙м. h =500 мм; сечение прямоугольное, шириной b =220 мм (полка в растянутой зоне – рис. 8, в); а =85 мм; h0 =415 мм.
Принято 2Æ14 А400 с А s=308 мм2 (+13,2%). г) Средние опоры С. Мс=- 91,58 кН∙м ;h =500 мм; сечение прямоугольное, шириной b =220 мм(полка в растянутой зоне – рис. 8, б); а =35 мм; h0= 465 мм.
Принято: 2Æ16 А400 + 2Æ14 А400 с Аs =402+308=710 мм 2 (+8,1%). д) Крайняя опора А. Требуемая площадь рабочей арматуры в гнутой опорной сетке (рис. 7): АsопА≥0,25Аs1=0,25∙876,5=219,1 мм2 Принято: 2Æ12 А400 с Аs =226 мм2 (+3,1%). Расчет балки на прочность по наклонным сечениям Крайний пролёт Расчёт на а) Проверка прочности по наклонной сжатой полосе
т.е. прочность наклонной сжатой полосы обеспечена б) Проверка прочности наклонных сечений. Предварительно принимаем в качестве поперечной арматуры Æ6 А400 с шагом
Поскольку
Определение длины проекции невыгоднейшего наклонного сечения С:
Поскольку
Принимаем С =1263,2 мм <
Тогда
т.е. прочность наклонных сечений у опоры В слева обеспечена. Проверка требования Средний пролёт Расчёт на а) Проверка прочности по наклонной сжатой полосе
т.е. прочность наклонной сжатой полосы обеспечена б) Проверка прочности наклонных сечений. Предварительно принимаем в качестве поперечной арматуры Æ6 А400 и её шаг
Поскольку
Поскольку
Принимаем С=1254,7 <
Тогда
т.е. прочность наклонных сечений у опоры В справа обеспечена. Проверка требования Расчёт на Принимаем шаг Sw1= 200 мм
Поскольку С = 1263,2 мм С0 = 886 мм;
Увеличить Sw1 до 225мм нельзя из-за конструктивных требований Sw1 Определение длин приопорных участков В средней части пролётов балки шаг хомутов может быть увеличен до значения:
Так как
длина приопорных участков определяется по формуле
Где для крайнего пролёта
У опоры А Qmax=QА=106,57 кН
У опоры В слева Qmax=Qbл=159,85 кН
Средний пролёт Qmax= Qbл = Qс=133,21 кН
Графический способ
Длины приопорных участков принимаются большими из двух полученных расчетным и графическим методами значений, т.е. в нашем случае соответственно 1.4, 2.5 и 2.0 м
ПРИМЕР 1.3 Вариант армирования отдельными стержнями. Требуется рассчитать на прочность второстепенную балку монолитного железобетонного междуэтажного ребристого перекрытия при разбивке балочной клетки по рис. 2.
Дополнительные исходные данные Коэффициент снижения временной нагрузки для второстепенной балки к3 =1,0 (по заданию). Продольная рабочая арматура класса А400 (рис.5, б) с рабочей арматурой также класса А400. Класс поперечной арматуры подбирается из условия экономичности (по расходу материала). Расчетное сопротивление тяжелого бетона класса В15 с учетом коэффициента условий работы γb1 =1,0 равно Rb =8,50 МПа, Rbt =0,75 МПа. Предварительно принятые размеры сечения второстепенной балки: bВ =220 мм; hВ =500мм; шаг балок в осях S = 2,0 м; толщина плиты hп = 80 мм (см. Пример 1.1). По рекомендациям п. 2.2 настоящих указаний назначаем размеры сечения главной балки: высоту – hr = 1/9 l = 1/9∙6000=667 мм, принимаем hr =700 мм > hВ +150 мм =500+150=650 мм; ширину – bГ =(0,4-0,5) hr =(0,4-0,5)∙700=280-350 мм, принимаем bГ =300 мм. 7. Расчетные пролеты второстепенной балки (рис. 4, в) l1=lк - bГ =5,8-0,3=5,5 м. Расчетные нагрузки а) Постоянная (при γf =1,1 и γn =1,0). Расчетную нагрузку g0 от собственного веса плиты и веса пола и перегородок принимаем по подсчетам, выполненным в Примере 1.1: g0 =4,95 кН/м2. Расчетная погонная нагрузка от собственного веса ребра балки, расположенного ниже плиты: gp = γf (hВ - hП)∙ bВ ·ρ=1,1∙(0,50-0,08)∙0,22∙25=2,54 кН/м. Расчетная постоянная нагрузка с учетом коэффициента надежности по ответственности здания γn =1,0 равна: gp = γn∙ (g0∙S + gP)=1,0∙(4,95∙2,0+2,54)=12,44 кН/м б) Временная расчётная погонная нагрузка (при γf =1,2; к3 =1,0 и γn =1,0) составит: р = γn∙к3∙ γf рn∙S =1,0∙1,0∙1.2∙15∙2,0=36,0 кН/м. в) Полная расчетная погонная нагрузка на балку: q = g+р =12,44+36,0=48,44 кНм. 9. Расчетные изгибающие моменты (рис. 4,б) В крайнем пролете:
На второй с края опоре В:
В средних пролетах: а) положительный момент
б) отрицательный момент между точками 6 и 7
Значения коэффициента β при p/g =3 по табл. 1: для точки 6: β6 =–0,035; для точки 7: β7 =–0,016. Для определения момента М6-7:
М6-7 = β∙q∙l12 =-0,0255∙48,44∙5,52=-37,37 кН∙м. На средних опорах С: Мc =- М2 =-91,58 кН/м. 10. Расчетные поперечные силы по граням опор (рис. 4,в) На крайней опоре А: QA На второй с края опоре В слева: QЛВ На опоре В справа и на всех средних опорах С: QПВ = QC =0,5 q∙l1 =0,5∙48,44∙5,5=133,21 кН.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.32.243 (0.007 с.) |

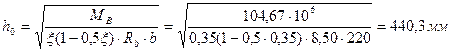 Значение а принимаем равным 40 мм (рис. 8, б).
Значение а принимаем равным 40 мм (рис. 8, б).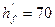 мм
мм 
 мм.
мм.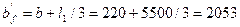 мм;
мм; мм < 2053 мм.
мм < 2053 мм. мм.
мм.

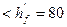 мм, т.е. нейтральная ось действительно находится в полке.
мм, т.е. нейтральная ось действительно находится в полке. мм 2.
мм 2.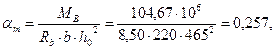

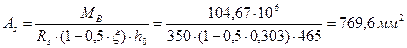
 мм;
мм; мм
мм  мм.
мм. мм.
мм.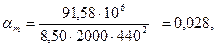
 ;
; мм,
мм,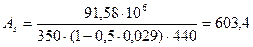 мм 2.
мм 2.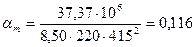 ; ξ =0,124;
; ξ =0,124;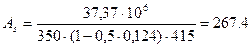 мм 2.
мм 2. , ξ= 0,260,
, ξ= 0,260,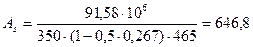 мм 2.
мм 2.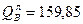 кН
кН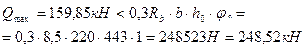
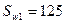 мм
мм 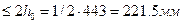
 Н/мм
Н/мм т.е. условие
т.е. условие  соблюдается хомуты полностью учитываются в расчёте и
соблюдается хомуты полностью учитываются в расчёте и  определяется по формуле:
определяется по формуле: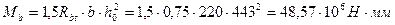
 кН/ м(Н/мм)
кН/ м(Н/мм)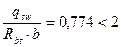 ,значение С определяется по формуле:
,значение С определяется по формуле: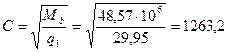 мм
мм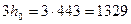 мм
мм

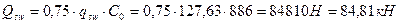
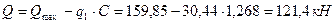
 ,
,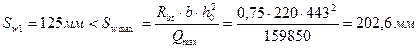
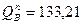 кН
кН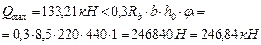
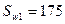 мм.
мм.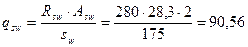 Н/мм
Н/мм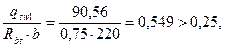 т.е. условие
т.е. условие 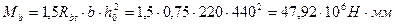
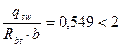 , значение С определяется по формуле:
, значение С определяется по формуле: мм
мм мм
мм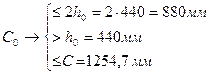 , принимаем С 0=870 мм.
, принимаем С 0=870 мм.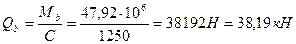

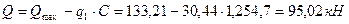

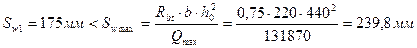
 кН
кН . Поскольку
. Поскольку то есть хомуты полностью учитываются в расчете и
то есть хомуты полностью учитываются в расчете и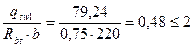 , значение С определяется по формуле
, значение С определяется по формуле  . Принимаем
. Принимаем 3 h0= 1329 мм.
3 h0= 1329 мм.



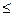 0,5 h0=0,5* 443= 221,5 мм
0,5 h0=0,5* 443= 221,5 мм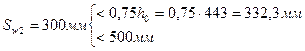
 Н/мм
Н/мм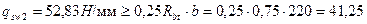 Н/мм
Н/мм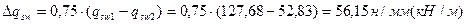
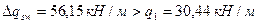 ,
, ,
,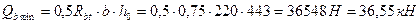
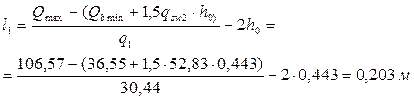
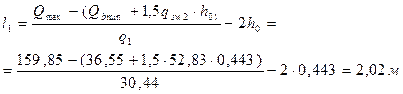
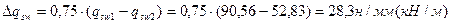 Так как
Так как 
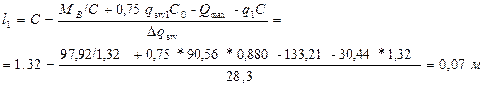


 кН∙м;
кН∙м;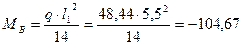 кН∙м;
кН∙м;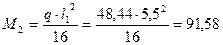 кН∙м;
кН∙м;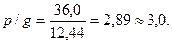

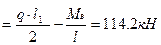
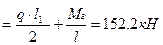 .
.


