Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет на прочность наклонных сеченийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Балки по поперечной силе Q Сущность методики расчета прочности наклонных сечений на действие поперечной силы Q заключается в проверке прочности сжатой полосы между наклонными трещинами и прочности по самому наклонному сечению. За расчетное сечение принимается наклонное сечение, начинающееся у грани опоры и заканчивающееся в сжатой зоне на расстоянии с от грани опоры. В дальнейшее через с обозначается длина проекции на продольную ось элемента расчетного наклонного сечения (рис. 9). Через с0 обозначается длина проекции на продольную ось элемента наклонной трещины. Наибольшее значение поперечной силы Qmax в пределах расчетного наклонного сечения будет у грани опоры.
Расчет на поперечную силу сводится к проверке прочности элемента по наклонному сечению при принятых по конструктивных соображениям, основанным на требованиях СНиПа, диаметре и шаге поперечных стержней и размещении их по длине пролета. Диаметр поперечных стержней dsw сварных каркасов принимается по табл. П. 7 приложения в зависимости от выбранного из расчета на момент диаметра продольной арматуры d из условия обеспечения доброкачественной точечной сварки. Число n поперечных стержней в нормальном сечении равно числу принятых плоских сварных каркасов. Например, в сборной плите в каждой продольном ребре ставится по одному плоскому каркасу, поэтому общее число поперечных стержней в сечении будет равно двум (n =2). Количество поперечных стержней в нормальном сечении сборного ригеля будет указано ниже при расчете этого элемента. При загружении изгибаемого элемента равномерно распределенной нагрузкой шаг поперечных стержней s принимается на основании следующих конструктивных требований (см. Рис. 4 настоящего пособия): - на приопорных участках шаг s1£ h0/ 2 и £ 30 0 мм, - на среднем участке шаг s2 £ ¾ h0 и £ 500 мм, где h 0 – рабочая высота сечения элемента После назначения диаметра, шага поперечных стержней и их размещения по длине пролета производится проверка прочности по наклонному сечению на действие поперечной силы. Расчёт изгибаемых элементов из тяжёлого бетона по бетонной полосе между наклонными сечениями производится из условия
где Q - поперечная сила в нормальном сечении, проходящем на расстоянии от опоры не менее h 0; Расчёт по наклонному сечению производится из условия
где Q - поперечная сила в нормальном сечении, проходящем на расстоянии С от опоры; Qв- поперечная сила, воспринимаемая бетоном в наклонном сечении; Qsw- поперечная сила, воспринимаемая хомутами (поперечными стержнями) в наклонном сечении;
Здесь
где C 0-длина проекции наклонной трещины, принимаемая равной С, но не более 2 h 0. Хомуты учитываются в расчёте, если соблюдается условие При расчёте элемента на действие равномерно распределенной нагрузки q, значение С принимается равным
При этом значение Q принимается равным где Q max-поперечная сила в опорном сечении. Диаметр поперечной арматуры принимают не менее 0,25 наибольшего диаметра продольной арматуры и ≥ 6 мм в случае вязанных каркасов. В случае необеспеченности по расчёту прочности наклонного сечения при первоначально принятых исходных данных (S 1, d sw), требуется или увеличить диаметр поперечных стержней или уменьшить их шаг и выполнить повторный проверочный расчёт на Q. Как и при проектировании других балочных изгибаемых элементов, длины приопорных участков l 1 второстепенной балки, на которых следует размещать поперечные стержни с учащённым шагом S 1 принимается большим из двух величин, определённым теоретическим и графическим способом. Фактическая же длина этих приопорных участков окончательно устанавливается при конструировании каркасов - при разбивке шагов их поперечных стержней, но не менее расчётных. При действии на элемент равномерно распределенной нагрузки длина участка с интенсивностью хомутов q sw принимается не менее значения l 1 определяемого в зависимости от если
где При этом, однако, если Если где Если значение Шаг хомутов, учитываемых в расчёте, должен быть не более значения:
Если ПРИМЕР 1.2 Вариант армирования сварными каркасами и сетками. Требуется рассчитать на прочность второстепенную балку монолитного железобетонного междуэтажного ребристого перекрытия при разбивке балочной клетки по рис. 2. Дополнительные исходные данные Коэффициент снижения временной нагрузки для второстепенной балки к3 =1,0 (по заданию). Продольная рабочая арматура пролетных сварных каркасов – класса А400. Опоры балки армируются гнутыми сварными сетками (рис.5, б; 6 и 7) с рабочей арматурой также класса А400. Класс поперечной арматуры подбирается из условия экономичности (по расходу материала). Расчетное сопротивление тяжелого бетона класса В15 с учетом коэффициента условий работы γb1 =1,0 равно Rb =8,50 МПа, Rbt =0,75 МПа. Предварительно принятые размеры сечения второстепенной балки: bВ =220 мм; hВ =500мм; шаг балок в осях S = 2,0 м; толщина плиты hп = 70 мм (см. Пример 1.1). По рекомендациям п. 2.2 настоящих указаний назначаем размеры сечения главной балки: высоту – hr = 1/9 l = 1/9∙6000=667 мм, принимаем hr =700 мм > hВ +150 мм =500+150=650 мм; ширину – bГ =(0,4-0,5) hr =(0,4-0,5)∙700=280-350 мм, принимаем bГ =300 мм. 1. Расчетные пролеты второстепенной балки (рис. 4, а) l1=lк - bГ =5,8-0,3=5,5 м. Расчетные нагрузки а) Постоянная (при γf =1,1 и γn =1,0). Расчетную нагрузку g0 от собственного веса плиты и веса пола и перегородок принимаем по подсчетам, выполненным в Примере 1.1: g0 =4,95 кН/м2. Расчетная погонная нагрузка от собственного веса ребра балки, расположенного ниже плиты: gp = γf (hВ - hП)∙ bВ ·ρ=1,1∙(0,50-0,08)∙0,22∙25=2,54 кН/м. Расчетная постоянная нагрузка с учетом коэффициента надежности по ответственности γn =1,0 равна: gp = γn∙ (g0∙S + gP)=1,0∙(4,95∙2,0+2,54)=12,44 кН/м б) Временная расчётная погонная нагрузка (при γf =1,2; к3 =1,0 и γn =1,0) составит: р = γn∙к3∙р0∙S =1,0∙1,0∙18∙2,0=36,0 кН/м. в) Полная расчетная погонная нагрузка на балку: q = g+р =12,44+36,0=48,44 кНм. 3. Расчетные изгибающие моменты (рис. 4,б) В крайнем пролете:
На второй с края опоре В:
В средних пролетах: а) положительный момент
б) отрицательный момент между точками 6 и 7
Значения коэффициента β при p/g =3 по табл. 1: для точки 6: β6 =–0,035; для точки 7: β7 =–0,016. Для определения момента М6-7:
М6-7 = β∙q∙l12 =-0,0255∙48,44∙5,52=-37,37 кН∙м. На средних опорах С: Мc =- М2 =-91,58 кН/м. 4. Расчетные поперечные силы по граням опор (рис. 4,в) На крайней опоре А: QA =0,4 q∙l1 =0,4∙48,44∙5,5=106,57 кН На второй с края опоре В слева: QЛВ =0,6 q∙l1 =0,6∙48,44∙5,5=159,85 кН. На опоре В справа и на всех средних опорах С: QПВ = QC =0,5 q∙l1 =0,5∙48,44∙5,5=133,21 кН.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 425; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.140.108 (0.012 с.) |

 ,
,
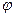 n
n , где
, где  . Значение Qb принимается не более 2,5 Rbtbh 0 и не менее 0,5 Rbtbh 0.
. Значение Qb принимается не более 2,5 Rbtbh 0 и не менее 0,5 Rbtbh 0. ,
, - усилие в хомутах на единицу длины элемента;
- усилие в хомутах на единицу длины элемента; . Если нет, то Мb принимается равным
. Если нет, то Мb принимается равным  .
. , а если при этом
, а если при этом  или
или  ,следует принимать
,следует принимать 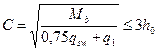 , где погонная нагрузка
, где погонная нагрузка  или
или  ø
ø ,
, следующим образом:
следующим образом: , то:
, то: ,
, принимается не более 3 h 0.
принимается не более 3 h 0. , то принимается
, то принимается 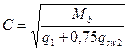 ;
; , то
, то  ,
,
 , длина l 1 вычисляется при
, длина l 1 вычисляется при  и
и  При этом сумма (
При этом сумма ( ) принимается не менее нескорректированных значений Qb ,min.
) принимается не менее нескорректированных значений Qb ,min. и не более значения по конструктивным требованиям.
и не более значения по конструктивным требованиям. , шаг хомутов принимается без расчёта по конструктивным требованиям.
, шаг хомутов принимается без расчёта по конструктивным требованиям. кН∙м;
кН∙м;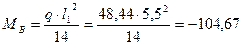 кН∙м;
кН∙м;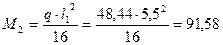 кН∙м;
кН∙м;