
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подбор сечения прогона из прокатного профиля (швеллер)Содержание книги
Поиск на нашем сайте Пример выполнения расчётной части Курсового проекта В. Пименов, В. Ячменёв, КГТУ, кафедра ПГС КГТУ, Калининград. Версия-2013
Схема фермы - №1 Пролёт фермы - L=16 м Длина панели верхнего пояса - d=2,0 м Левая опорная стойка - h0 =2,0 м Уклон - i=1/8 Шаг ферм - l =6 м Сталь марки - 10 ХСНД Постоянные нормативные нагрузки,, кН/м2 p1; p2; p3; p4 (см. табл.1)
Нормативная нагрузка от тельфера с Рис.1. Расчётная схема рамы грузом – Tn= 40 кН Высота колонны – Н = 10 м Район строительства – г. Киров
Покрытие производственного здания выполнить по прогонам из прокатного профиля. Кровля из панелей типа "сэндвич" с толщиной утеплителя согласно заданию. Снеговая нагрузка - по району строительства.
1. Сбор нагрузки на 1 м2 кровли Нагрузки представлены в табличной форме (см. таблицу 1.). Временная (снеговая) расчётная нагрузка на 1 м2 кровли определяется по формуле
s = s0∙μ= 3,2∙1 = 3,2 кН/м2 где: s0 - расчётное значение веса снегового покрова на 1 м2 горизонтальной поверхности, принимаемого по (табл. 10.1. СНиП 2.01.07 -85*) в зависимости от района строительства Заданный район строительства – г. Киров. Это V-й снеговой район, для которого s0 = 3,2 кН/м2; μ – коэффициент перехода от веса снегового покрова к снеговой нагрузке на покрытие, зависящий от очертаний кровли. Для бесфонарных зданий с уклоном кровли ≤ 25°, μ = 1. Нормативная временная (снеговая) нагрузка - sn= s/γn, где γn =0,7 - коэффициент надёжности при расчётах нормативной нагрзки.
Толщина утеплителя (минеральная вата плотностью ρ = 200 кг/м3) принимается в зависимости от района строительства. Для снеговых районов I и II, δ=100 мм; для снеговых районов III и IV, δ=200 мм и для V-го снегового района, δ=300 мм. Нормативная нагузка на 1 м2 кровли от утеплителя, толщиной 100 мм - p3= 0,2 кН/м2.
Нрмативная нагрузка на 1 м2 кровли от веса прогонов на первом этапе принимается как 10% от суммы постоянных нагрузок за исключением прогонов, т.е.
p4 = 0,1(p1+p2+p3) Сбор нагрузки на 1 м2 кровли Таблица 1.
Подбор сечения прогона из прокатного профиля (швеллер) Расчётная схема прогона - балка, свободно опёртая на две соседних фермы и загруженная погонной нагрузкой от веса кровли и веса снега.
Нормативная погонная нагрузка на один прогон, кН/м: qn = (pn + sn) ∙d =(1,05 + 2,24) ∙2,0 = 6,58; Расчётная погонная нагрузка на один прогон, кН/м: q = (p + s) ∙d =(1,19 + 3,20) ∙2,0 = 8,78; здесь: d=2,0 м - длина панели верхнего пояса (расстояние между узлами верхнего пояса.
Максимальный изгибающий момент в середине пролёта прогона:
Mmax = q∙l2 /8 = 8,78∙62/8 =39,5 кН∙м = 3950 кН∙см; где l =B =6 м - расстояние между фермами (пролёт прогона)
Требуемый момент сопротивления сечения прогона определяем из условия прочности при изгибе по формуле: σ = или - Wтр здесь: Ry = 34,5 кН/см2 -расчётное сопротивление по пределу текучести для стали марки 10 ХСНД (С375) при толщине фасонного проката 10...20 мм (табл.51 СНиП II-23-85*); γc =1 -коэффициент условий работы.
По требуемому моменту сопротивления Wтр = 114 см3 по сортаменту подбираем швеллер №18 по ГОСТ 8240-72, характеристики которого: момент инерции - Jx =1090 см4; момент сопротивления - Wx = 121 см3; масса 1 пог.м - mпог = 16,3 кг.
Проверяем для выбранного сечения соблюдения условия жёсткости по формуле:
fmax = где: - fmax -максимальный прогиб (в середине пролёта прогона);
[f] =
qn = 6,58 кН/м = 0,0658 кН/см - нормативная погонная нагрузка;
l =B =6 м = 600 см - расстояние между фермами (пролёт прогона); Е = 2,06∙104 кН/см2 - модуль упругости стали;
Jx =1090 см4 -момент инерции сечения.
Так как fmax = 4,94 см ˃ [f] = 3,0 см, назначаем швеллер болшего размера, т.е. №22, характеристики которого: момент инерции - Jx =2110 см4; момент сопротивления - Wx = 192 см3; масса 1 пог.м - mпог = 21,0 кг.
Тогда максимальный прогиб
fmax = Узловые нагрузки Нагрузка на каждый узел верхнего пояса (узловая нагрузка), за исключением узлов над опорами фермы, от веса кровли (постоянная расчётная нагрузка):
Fg = pфакт ∙ l∙ d = 1,20∙6∙2 =14,4 кН Узловая нагрузка от веса кровли на крайние узлы - 0,5 Fg = 0,5∙14,4 = 7,2 кН Здесь и далее, l иd - соответственно пролёт прогона и длина панели верхнего пояса (расстояние между узлами), м. Нагрузка на каждый узел верхнего пояса (узловая нагрузка), за исключением узлов над опорами фермы, от веса снегового покрова (временная расчётная нагрузка):
Fs = s ∙ l∙ d = 3,20∙6∙2 =38,4 кН Здесь, s -расчётная снеговая нагрузк на 1 м2 кровли, кН/м2. Узловая нагрузка от веса снега на крайние узлы - 0,5 Fs = 0,5∙38,4 = 19,2 кН Суммарная узловая нагрузка (вес кровли + вес снега)
F = Fg + Fs = 14,4 + 38,4 = 52,8 кН 0,5F = 0,5∙52,8 =26,4 кН Суммарную узловую нагрузку (вес кровли + вес снега) применять при аналитическом расчёте усилий в стержнях фермы. Расчёт фермы Расчёт усилий в стержнях фермы проводится либо графоаналитическим методом Максвелла-Кремоны, либо аналитическим методом, по выбору студента.
В первом случае строятся две диаграммы Максвелла-Кремоны, отдельно для постоянной и снеговой нагрузки и отдельно от тельферной нагрузки, причём в обоих случаях нагрузка прикладывается только к одной половине фермы. Так как постоянная нагрузка не меняет своего положения, рассматриваются рассматриваются следующие сочетания нагрузок: снег на левой половине -тельфер на левой половине; снег на правой половине -тельфер на левой половине; снег на левой половине -тельфер на правой половине; снег на правой половине -тельфер на правой половине. Это делается из-за того, что усилия в некоторых раскосах и стойках могут поменять знак. Усилия в поясах при любых сочетаниях нагрузок знак не меняют. Так усилия в стержнях верхнего пояса всегда имеют знак "минус" (сжатие), а усилия в стержнях нижнего пояса всегда иеют знак "плюс" (растяжение).
При выборе аналитического метода, расчёт усилий производится от полной нагрузки (постоянная + снеговая + тельферная). Учитывая симметрию самой фермы и нагрузки, расчёт проводится только для половиныфермы.
Методом Максвелла-Кремоны Проводим сечение I-I Рис.8. Узел 1. Проводим сечение I-I (см. рис.3 и рис.6). Сечение проводим таким образом, чтобы линия сечения пересекала не более 3-х стержней с неизвестными усилиями. Рассмотрим равновесие левой отсечённой части относительно узлов, в которых сходятся два стержня с неизвестными усилиями. Моменты всех сил относительно выбранных узлов должны равняться нулю. Рассмотрим равновесие левой отсечённой части (рис.9).
ΣМ3=0; (VA- 0,5F)∙d∙ cos γ + N3-5∙ cos γ∙h2=0; откуда N3-5 = [-(VA-0,5F)∙d]/h2 = [-(266- 0,5∙52,8)∙2,0]/2,248 = -213,2 кН
Сумма проекций всех сил на ось Y равна нулю: ΣY=0; VA - 0,5F - F + N3-5 ∙ sin γ + N2-5 ∙ sin α2 = 0, откуда: N2-5 = (1,5 F - VA - N3-5 ∙ sin γ)/ sin α2 = [1,5∙52,8 - 266 - (- 213,2)∙ sin 7,125°]/ sin 51,55° = - 160,3/0,7832 = -204,7 кН
Рис. 9. Левая отсечённая часть Сумма проекций всех сил на ось X равна нулю: ΣX=0;
N3-5 ∙ cos γ + N2-5 ∙ cos α2 + N2-4 = 0; откуда N2-4 = - N3-5 ∙ cos γ - N2-5 ∙ cos α2 = -(-213,2)∙ cos 7,125° - (-204,7)∙ cos 51,55° = 339 кН
N3-5 = - 213,2 кН; N2-5 = - 204,7 кН; N2-4 = 339 кН 5.2.3.4. Вырезаем узел 4 (рис.6 и рис.10) и рассматриваем его равновесие в проекциях сил на оси координат. ΣX=0; -N2-4 + N4-6 = 0; откуда N4-6 = N2-4 = 339 кН
ΣY=0; N4-5 - Т = 0, откуда N3-4 = Т = 54,8 кН
N4-6 = 339 кН; N4-5 = 54,8 кН
Рис. 10. Узел 4.
Рис.11. Левая осечённая часть
ΣМ6 = 0; (VA-0,5F)∙3d∙ cos γ -F∙2d∙cos γ – (F +T))∙d∙ cos γ + N5-7 ∙h3 ∙ cos γ + N5-7 ∙d ∙ sin γ = 0; откуда N5-7 = [-(VA-0,5F)∙3d∙ cos γ + F∙2d∙cos γ + (F + T)∙d∙cos γ]/(h3∙cos γ + d ∙ sin γ) = [-(266,0 – 26,4)∙3 + 52,8·2 + (52,8 + 54,8]∙2,0∙0,9923/(2,50·cos 7,125º + 2,0∙ sin 7,125º)· = = (- 718,8 + 105,6 + 107,6)·2·0,9923/(2,481 + 0,248) = - 1000/2,729 = - 366,4 кН Сумма проекций всех сил на ось Y равна нулю: ΣY=0; VA-0,5F – F –F – T + N5-7 ∙ sin γ – N5-6 ∙sin α2 = 0; откуда N5-6 = (VA-0,5F – F –F – T + N5-7 ∙ sin γ)/ sin α2 = (VA -2,5F - T + N5-7 ∙ sin γ)/sin α2 = [(266,0 - 2,5·52,8 – 54,8 + (-366,4)· sin 7,125º]/ sin 51,55º = 43,1 кН.
N5-7 = - 366,4 кН; N5-6 = 43,1 кН 5.2.3.6. Вырезаем узел 7 (рис.6 и рис.12) и рассматриваем его равновесие в проекциях сил на оси координат.
откуда N5-7 = N7-9 = - 366,4 кН;
ΣY=0; -N6-7 –F+ = 0, откуда N6-7 = - F = - 52,8 кН;
N6-7 = -52,8 кН; N5-7 = N7-9 = -366,4 кН
Рис.12. Узел 12.
5.2.3.7. Проводим сечение III-III (рис.6 и рис.13). Сечение проводим таким образом, чтобы линия сечения пересекала не более 3-х стержней с неизвестными усилиями. Рассмотрим равновесие левой отсечённой части. Рис.13. Сечение III - III. Левая отсечённая часть. Сумма проекций всех сил на ось Y равна нулю: ΣY=0;
VA - 3,5F - T + N7-9 ∙sin γ + N6-9 ∙sin α3 = 0, откуда N6-9 = - (VA - 3,5F - T + N7-9 ∙sin γ)/ sin α3 = -[266,0 - 3,5∙52,8 - 54,8 + (- 366,4)∙ sin 7,125º]/ sin 56,44° = 22,9 кН.
Сумма проекций всех сил на ось X равна нулю: ΣX=0;
N7-9 ∙ cos γ + N6-9 ∙ cos α3 + N6-8 = 0, откуда N6-8 = - N7-9 ∙ cos γ - N6-9 ∙ cos α3 = - (-366,4) ∙ cos 7,125°- 22,9 ∙ cos 56,44° = 351 кН
N6-9 = 22,9 кН; N7-9 = -366,4 кН; N6-8 = 351 кН.
ΣY=0; N8-8* = 0
Рис. 14. Узел 8 Расчётные длины стержней
Расчётные длины стержней для ферм из парных уголков назначаем по ([3], табл.1) и сводим в табл.4, представленную ниже. Таблица 5
Примечание: l – расстояние между узлами (теоретическая длина стержня); l
5.2.3.2. Назначение толщины фасонки.
Толщина узловых фасонок назначается в зависимости от усилий в стержнях решетки. Из стержней решетки наибольшим будет усилие в опорном раскосе или наибольшее усилие в ракосе всей решетки. По этому усилию и назначается толщина фасонки (табл. 2.3), которая может быть принята одинаковой во всех узлах фермы. Таблица 6
В нашем примере наибольшее усилие в опорном раскосе N1-2 = 300 кН, поэтому назначаем толщину фасонки t = 10 мм.
Опорный раскос.
Растягивающее усилие в опорном раскосе: N1-2 = 300 кН Величину требуемой площади сечения (пара уголков) находят по формуле: Атр = N1-2 / (Ry γc) = 300/(34,5·0,95) = 9,15 см Требуемая площадь сечения одного уголка – Атр1 = 9,15/2 = 4,6 см Предварительно, выбибираем равнополочный уголок 50×50×5 по ГОСТ 8509-86 (табл.П16.2, [4]), (уголки с шириной полки меньше 50 мм в фермах не применяются). Характеристики уголка, необходимые для расчёта: Площадь - А1 = 4,80 см Отстояние центра тяжести от обушка - Z0 = 1,42 см; Радиусы инерции: одиночного уголка – ix = 1,53 см Наименьшая гибкость это гибкость в плоскости фермы:
Гибкость в плоскости фермы λ = µ · l / ix = 1·282/1,53 = 184 < [λ] = 250
где µ ·=1 - коэффициент, учитывающиё сепень заделки концов стержня (в нашем случае это шарниры) l = R1-2 = 2,817 м = 282 см. Таким образом, для растянутых опорных раскосов окончательно назначаем равнополочный уголок 50×50×5 мм.
Центрально сжатые стержни.
Величину требуемой площади сечения (пара уголков) находят по формуле: Атр = N / (φ·Ry γc) где: φ – коэффциент продольного изгиба (см. табл.72 СНиП II-23-85); Ry - расчётное сопротивление по пределу текучести. Сталь марки 10 ХСНД соответствует обозначению стали С375 (табл.51 б, СНиП II-23-81). Стали С375 (фасонный прокат с толщинами св. 10 до 20 мм), соответствует Ry = 345 МПа, или, что более удобно для расчётов - Ry = 34,5 кН/см2. γc = 0,95 – коэффициент условий работы (нормальные условия).
Далее сравнивается гибкость стержня в плоскости и из плоскости изгиба фермы с предельной. Предельная гибкость при расчёте на динамическую нагрузку: для поясов, опорных раскосов и стоек, передающих опорные реакции и работающих на сжатие [λ] = 180-60α; для прочих элементов решетки, работающих на сжатие [λ] = 210-60α; Здесь: коэффициент α = N/(φ·A·Ry·γc), при этом должно выполняться условие α≥0,5 Предварительно задаются гибкостью (для поясов и опорных раскосов λ=60-80, для решетки λ=100-120)\
Верхний пояс. Nmax = │N5-7│= - 366,4 кН
Коэффициент продольного изгиба φ зависит о гибкости λ и от расчётного сопротивления Ry (см. табл.72 СНиП II-23-85), либо от значения приведенной гибкости -, определяемой по формуле: - = Е = 2,06·104 кН/см2 – модуль упругости стали. Рассмотрим оба этих случая:
1. Использование табл.72 СНиП II-23-85:
при Ry1 = 320 МПа (32,0 кН/см при Ry2 = 360 МПа (36,0 кН/см для Ry = 34,5 кН/см φ = φ = 0,687 – [(0,687-0,654)/(36,0-32,0)]·(34,5-32,0) = 0,666
φ = 0,67
2. Использование значения приведенной гибкости -: (Ю.И.Кудишин «Металлические конструкции», Приложение 8)
- = 0,041 λ = 0,041·70 = 2,9 При - = 2,8, φ = 0,673 При - = 3,0, φ = 0,628 Линейной интерполяцией получаем: φ = (0,673 + 0,628)/2 = 0,65 Как видно из рассмотренных примеров, значения φ различаются незначительно, но, объём вычислений гораздо меньше. Тогда Атр = 366,4 / (0,65·34,5 0,95) = 17,2 см Требуемая площадь сечения одного уголка – Атр1 = 17,2/2 = 8,6 см Предварительно, выбираем равнополочный уголок 75×75×6 по ГОСТ 8509-86 Характеристики уголка, необходимые для расчёта: Площадь - А1 = 8,78 см радиусы инерции: одиночного уголка относительно оси x(y) – ix = 2,3 см; составного сечения относительно оси y 1 не рассматриваем, т.к. он будет заведомо больше.
Гибкость в плоскости фермы λ = µ · l/ ix = 1·200/2,3 = 87 < [λ] = 105
где µ ·=1 - коэффициент, учитывающиё сепень заделки концов стержня (в нашем случае это шарниры) l = d = 200 см [λ] = 180-60α = 180-60·1,25 = 105;
где α = N/(φ·2A1·Ry·γc) = 366,4/(0,508·2·8,78·34,5·0,95) = 1,25 здесь: при - = 0,041·87 = 3,6 и φ = 0,508
Условие λ ≤ [λ] выполняется, поэтому для верхнего пояса окончательно назначаем равнополочный уголок 75×75×6 мм.
Раскос в районе тельферной балки N2-5 = -204,7 кН и длина раскоса R2-5 = 3,19 м = 319 см. Предварительно задаются гибкостью λ=70 и тогда - = 0,041 λ = 0,041·70 = 2,9 и, соответственно, φ = 0,65
Требуемая площадь пары уголков Атр = 204,7 / (0,65·34,5 0,95) = 9,6 см Требуемая площадь сечения одного уголка – Атр1 = 9,6/2 = 4,8 см Предварительно, выбираем равнополочный уголок 50×50×5 по ГОСТ 8509-86 (табл.П16.2, [4]). Характеристики уголка, необходимые для расчёта: Площадь - А1 = 4,88 см радиус инерции относительно оси x(y) – ix = 1,53 см
Гибкость в плоскости фермы λ= µ · R2-5/ ix = 1·319/1,53 = 208, что почти в три раза превышаеи исходную, поэтому назначаем уголок на три номера больше, т.е уголок 75 Характеристики уголка, необходимые для расчёта: Площадь - А1 = 8,78 см радиус инерции относительно оси x(y) – ix = 2,3 см
Гибкость в плоскости фермы λ= µ · R2-5/ ix = 1·319/2,3 = 139 ˃ [λ] = 101 Приведенная гибкость - = 0,041 λ = 0,041·139 = 5,7 Ближайшее табличное предельное значение - = 5,2 и соответственно φ = 0,27 [λ] = 180-60α = 180-60·1,32 = 101; где α = N/(φ·2A1·Ry·γc) = 204,7/(0,27·2·8,78·34,5·0,95) = 1,32
Так как условие λ ≤ [λ] не выполняется, увеличиваем сечение уголка и назначаем уголок 90х90х6 мм. Характеристики уголка, необходимые для расчёта: Площадь - А1 = 10,6 см радиус инерции относительно оси x(y) – ix = 2,78 см Гибкость в плоскости фермы λ= µ · R2-5/ ix = 1·319/2,78 = 115 < [λ] = 126 Приведенная гибкость - = 0,041 λ = 0,041·115 = 4,7 и φ = (0,340+0,312)/2=0,33 [λ] = 180-60α = 180-60·0,89 = 126; где α = N/(φ·2A1·Ry·γc) = 204,7/(0,33·2·10,6·34,5·0,95) = 0,89
Условие λ ≤ [λ] выполняется, поэтому окончательно назначаем уголок 90
Опорная стойка. NА-1 = -266 кН и длина стойки = h1 = 2,0 м = 200 см.
Предварительно задаются гибкостью λ=70 и тогда - = 0,041 λ = 0,041·70 = 2,9 и, соответственно, φ = 0,65
Требуемая площадь пары уголков Атр = 266 / (0,65·34,5 0,95) = 12,5 см Требуемая площадь сечения одного уголка – Атр1 = 12,5/2 = 6,25 см назначаем предварительно уголок 75 Характеристики уголка, необходимые для расчёта: Площадь - А1 = 8,78 см радиус инерции относительно оси x(y) – ix = 2,3 см
Гибкость в плоскости фермы λ= µ · h1 / ix = 1·200/2,3 = 87 < [λ] = 125 Приведенная гибкость - = 0,041 λ = 0,041·87 = 3,6 и φ = 0,508 [λ] = 180-60α = 180-60·0,91 = 125; где α = N/(φ·2A1·Ry·γc) = 266/(0,508·2·8,78·34,5·0,95) = 0,91
Условие λ ≤ [λ] выполняется, поэтому окончательно назначаем уголок 75 Сварные швы поясов Сварные швы поясов выполняются минимальным катетом через всю фасонку.
Верхний пояс выполнен из уголков 75×75×6 мм, поэтому, для пера катет шва k Для полуавтоматической сварки в среде СО2 минимальный катет при толщине наиболее толстого из свариваемых элементов t = 10 мм и пределе текучести до 380 МПа (38 кН/см2) по табл. 38* СНиП II-23-85 - kf = 5 мм = 0,5 см. Катет шва по обушку не более 1,2t =1,2∙0,6 = 0,7 см. Для того, чтобы не пренастраивать сварочный полуавтомат, оба шва (по перу и по обушку) выполняем единым катетом kf = 5 мм = 0,5 см. Нижний пояс выполнен из уголков 75×50×5 мм, поэтому, катет шва, учитывая требования выше, kf = 5 мм = 0,5 см. Длина сврных швов - по фасонке.
Расчёт стержня колонны.
Колонны промышленных зданий работают на внецентренное сжатие. Значения расчётных усилий (продольной силы N, изгибающего момента в плоскости рамы Mx и поперечной силы Q), определены по результатам статического расчёта рамы (см. п.6 выше). Расчётная длина в плоскости рамы определяется с учётом ряда упрощающих предпосылок: - колонна рассматривается как отдельно стоящий стержень с идеализированными условиями закрепления; - система загружается силами, приложенными только в узлах; - пространственная работа каркаса учитывается не в полной мере. Такой подход идёт в запас устойчивости.
Для колонны с постоянным по высоте сечением коэффициент расчётной длины m принимают в зависимости от способа закрепления колонны в фундаменте и соотношения погонных жесткостей ригеля и колонны. (см. СНиП II-23-85, п.6, табл.17а)
При жестком закреплении колонн в фундаменте (как в настоящем примере) m = При шарнирном закреплении ригеля к колонне n=0, тогда m= Сплошные колонны обычно проектируют двутаврового сечения. Для колонн с постоянным по высоте сечением применяются симметричные двутавры. Для снижения трудоёмкости изготовления колонн рационально применение прокатных профилей с параллельными гранями, типа Ш.
Последовательность подбора сечения сплошных колонн. Расчёт производим для левой стойки рамы (колонны), у которой изгибающий момент от горизонтальной нагрузки имеет наибольшую величину. 1. Находим коэффициент приведения m (он определён выше, m=2,0 2. Определяем расчётные длины lx и ly: lx = ly = m× l =2×10 =20 м =2000 см, где l =H=10 м – высота колонны; 3. Задаёмся высотой сечения колонны. При высоте Н до 12 м, h=Н/15 =1000/15=66,7 см. По сортаменту ГОСТ 26020-83, предварительно выбираем широкополочный двутавр 70Ш1, геометрические характеристики которого: h=683 мм – высота сечения; А=216,4 см2 – площадь сечения; Ix= 172000 см4 - момент инерции площади поперечного сечения относительно оси x; Wx= 5036 см3 – момент сопротивления площади сечения относительно оси x; ix =28,19 см – радиус инерции относительно оси x; Iy = 10400 см4 - момент инерции площади поперечного сечения относительно оси y; iy =6,93 см – радиус инерции относительно оси y; b=320 мм – ширина полки; s=13,5 мм – толщина стенки; t=19,0 мм –толщина полки.
4. Определяем условную гибкость
mx = eA/Wx где e – эксцентриситет, определяемый выражением e=Mmax/N e=110,5/266=0,415 м=41,5 см; mx= 41,5×216,4/5036 =1,78 здесь: Mmax=110,5 кН×м – максимальный изгибающий момент в колонне; N = 266 кН – центрально приложенная сжимающая продольная сила, равная опорной реакции фермы. 5. По полученным значениям mx и Предварительно опредеяем соотношение Af /Aw =608/926 = 0,66 где: Af = b∙t = 32∙19,0 = 608 см2 - площадь полок двутавра; Aw = h∙s =68,3∙13,5 = 926 см2;
При mx = 1,78 и при Af /Aw =0,66 и
h = (1,75-0,1mx) – 0,02(5-mx) Приведенный относительный эксцентриситет mef=h×mx = ×094•1,78=1,67 при
при при при
Требуемая площадь сечения
Атр = N / (φe·Ry γc) = 266/(0,435×34,5×0,95) =18,7 см2 ˂ 216,4 см2, поэтому можно назначить двутавр меньшего размера. Назначаем двутавр 40Ш1, для которого:
h=388 мм – высота сечения; А=122,4 см2 – площадь сечения; Ix= 34360 см4 - момент инерции площади поперечного сечения относительно оси x; Wx= 1771 см3 – момент сопротивления площади сечения относительно оси x; ix =16,76 см – радиус инерции относительно оси x; Iy = 6306 см4 - момент инерции площади поперечного сечения относительно оси y; iy =7,18 см – радиус инерции относительно оси y;
Далее проводим повторный расчёт
Определяем условную гибкость
mx = eA/Wx где e – эксцентриситет, определяемый выражением e=Mmax/N e=110,5/266=0,415 м=41,5 см; mx= 41,5×122,4/1771 =2,9 По полученным значениям mx и При mx = 2,9 и при Af /Aw =0,5 и h = (1,75-0,1mx) – 0,02(5-mx) Приведенный относительный эксцентриситет mef=h×mx = 1,25×2,9=3,6 при
при при при
Требуемая площадь сечения Атр = N / (φe·Ry γc) = 266/(0,160×34,5×0,95) =50,7 см2 ˂ 122,4 см2. Так как требуемая площадь практически в 2 раза меньше чем у принятого двутавра, берём двутавр 35Ш1, для которого:
h=338 мм – высота сечения; А=95,67 см2 – площадь сечения; Ix= 19790 см4 - момент инерции площади поперечного сечения относительно оси x; Wx= 1171 см3 – момент сопротивления площади сечения относительно оси x; ix =14,38 см – радиус инерции относительно оси x; Iy = 3260 см4 - момент инерции площади поперечного сечения относительно оси y; iy =5,84 см – радиус инерции относительно оси y; bf=250 мм – ширина полки; s=9,5 мм – толщина стенки; tf=12,5 мм –толщина полки.
Далее проводим повторный расчёт
Определяем условную гибкость
mx = eA/Wx где e – эксцентриситет, определяемый выражением e=Mmax/N e=110,5/266=0,415 м=41,5 см; mx= 41,5×95,6/1171 =3,4 По полученным значениям mx и При mx = 3,4 и при Af /Aw =0,5 и h = 1,25 Приведенный относительный эксцентриситет mef=h×mx = 1,25×3,4=4,25 при
при при при
Требуемая площадь сечения Атр = N / (φe·Ry γc) = 266/(0,124×34,5×0,95) =65,5 см2 ˂ 95,67 см2.
6. Проверяем устойчивость колонны из плоскости изгиба
Требуемая площадь сечения Атр = N / (φ·Ry γc) = 266/(0,158×34,5×0,95) =51,4 см2 ˂95,67 см2 у принятого двутавра. где j = 0,158 (получено интерполяцией значений по табл.72, СНиП II-23-85), при l = ly / iy = 1000/5,84 =170 Устойчивость колонны из плоскости изгиба обеспечена. Расчёт оголовка колонны
Конструктивное решение опорного узла фермы дано на Рис.16. Здесь нет явно выраженного опорного ребра. Его роль играет фасонка и уголки стойки фермы. На этом же рисунке дано конструктивное решение оголовка. Строганную плиту толщиной tpl = 20 мм привариваем к фрезерованному торцу стержня колонны угловыми швами катетом kf = 7 мм (см. табл. 38* СНиП II-23-81*). Размеры плиты в плане 280х380 мм, т.е края плиты выступают за габарит сечения колонны на 20 мм с каждой стороны по высоте сечения и на 15 мм по ширине. Ширину опорных рёбер принимаем не менее
br ≥ bh /2 + tpl -tw /2 = 160/2 + 20 - 9,5/2 = 95,25 мм. Назначаем br = 100 мм,где
bh = 75+75+10 = 160 мм - габарит сечения оорного узла по ширине фермы. Здесь 75 мм - ширина полки уголка, 10 мм - толщина фасонки.
Рёбра и плиту проектируем из стали С235 (учитывая относительно небольшую нагрузку на ферму), для которой Rp = Ru = 35 кН/см2 (см. табл. 51а СНиП II-23-81*). Здесь Rp = Ru -расчётное сопротивление смятию, равное расчётному сопротивлению попределу прочности. Расчётная длина сминаемой поврхности рёбер равна:
lef = bh + tpl = 160 + 20 = 180 мм = 18 см.
Рис.16. Проектирование оголовка колонны
Толщину рёбер оголовка определяем по формуле
tr = N /(lef ∙∙Rp ∙γc) = 266/(18∙35∙1) = 0,42 см = 4,2 мм. Принимая во внимание, что основная нагрузка через 2 плиты действует на стенку колонны, и роль ребра в опорном узле играет фасонка, необходимость в рёбрах отпадает. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 ≤ Ry∙ γc -откуда требуемый момент сопротивления: Wтр
≤ Ry∙ γc -откуда требуемый момент сопротивления: Wтр  Mmax /(Ry ∙ γc)
Mmax /(Ry ∙ γc) 3950/(34,5 ∙ 1) = 114 см3
3950/(34,5 ∙ 1) = 114 см3 =
=  = 4,94 см ˃ [f] =
= 4,94 см ˃ [f] =  =
=  =3,0 см;
=3,0 см; - нормируемый (допускаемый) прогиб.
- нормируемый (допускаемый) прогиб. = 2,55 см ˂ [f] = 3,0 см
= 2,55 см ˂ [f] = 3,0 см


 ;
; = λ·
= λ·  = 0,041 λ где:
= 0,041 λ где: λ=70, φ
λ=70, φ  = 0,654
= 0,654 6 мм.
6 мм. 90х
90х  = t-1 мм = 6 -1 = 5 мм (0,5 см).
= t-1 мм = 6 -1 = 5 мм (0,5 см). ;
; =2,0
=2,0 x и относительный эксцентриситет mx
x и относительный эксцентриситет mx = (2000/28,19)
= (2000/28,19) 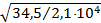 =2,9
=2,9 x =4,05 и mef = 1,67 je определяем интерполяцией:
x =4,05 и mef = 1,67 je определяем интерполяцией:



