
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрические характеристики приведенного сеченияСодержание книги
Поиск на нашем сайте
Круглое очертание пустот заменяется эквивалентным квадратным со стороной с = 0,9· d = 0,9·15,9 = 14,3 см. Размеры расчетного двутаврового сечения: толщина полок: h’ƒ = hƒ = (22 – 14,3)·0,5 = 3,85 см; ширина ребра b = 146 – 14,3·7 = 45,9 см; ширина полок b’ƒ =146 см; bƒ = 149 см. Определяем геометрические характеристики приведенного сечения: α = Es/Eb = (2·106)/31,8·104 = 6,29. Площадь приведенного сечения: Ared = A + αAs = b’ƒ ·h’ƒ + bƒ ·hƒ + b·c + αAs = (146 + 149)·3,85 + 45,9·14,3 + 6,29·5,6 = 1135,75 + 656,37 + 35,22 = 1827,34 см2; А = 1792,12 см2 – площадь сечения бетона. Статический момент приведенного сечения относительно нижней грани: Sred = b’ƒ ·h’ƒ· (h + 0,5·h’ƒ) + bƒ ·hƒ · 0,5·hƒ + b·c·0,5·h + α·As·a = = 146·3,85·(22 – 0,5·3,85) + 149·3,85·0,5·3,85 + 45,9·14,3·0,5·22 + 6,29·5,6·3 = = 11284,16 + 1104,28 + 7220,07 + 105,67 = 19714,18 см3. Удаление центра тяжести сечения от его нижней грани: y0 = Sred/Ared = 19714,18/1827,34 = 10,788 ≈ 10,8 см. Момент инерции приведенного сечения относительно его центра тяжести: Ired = = 108296,23 см4 Момент приведенного сечения по нижней грани: Wred = Ired/y0 = 108296,23/10,8 = 10027,43 см3. То же, по верхней грани:
Расчет предварительно напряженных изгибаемых элементов по раскрытию трещин производят в тех случаях, когда соблюдается условие: M > Mcrc M – изгибающий момент от внешней нагрузки (нормативной); Mcrc – изгибающий момент, воспринимаемый нормальным сечением элемента при образовании трещин и равный: Mcrc = Rbt,ser ·W + P·e яр, где W – момент сопротивления приведенного сечения для крайнего растянутого волокна; еяр = еор + r – расстояние от точки приложения усилия предварительного обжатия до ядровой точки, наиболее удаленной от растянутой зоны; еор – то же, до центра тяжести приведенного сечения; r - расстояние от центра тяжести приведенного сечения до ядровой точки; W = 1,25 · Wred для двутаврового симметричного сечения; P – усилие предварительного обжатия с учетом потерь предварительного напряжения в арматуре, соответствующих рассматриваемой стадии работы элемента. Определяем: r = Wred/Ared = 10027,43/1827,34 = 5,49 см; еор = y0 – a = 10,8 – 3 = 7,8 см; еяр = 7,8 + 5,49 =13,29 см; W = 1,25·10027,43 = 12534,3 см3. Потери предварительного напряжения арматуры. Потери от релаксации напряжений арматуры Δσsp1определяют для арматуры класса А600 при электромеханическом способе натяжении в соответствии с п.2.2.3.3 СП 52-102-2004. Δσsp1 = 0,03· σsp = 0,03·4880 = 146, 4 кг/см2. Потери от температурного перепада при агрегатно-поточной технологии принимаются равными 0; Δσsp2 = 0. Потери от деформации формы при электротермическом способе натяжения арматуры не учитывают; Δσsp3 = 0. Потери от деформации анкеров при электротермическом способе натяжения арматуры не учитывают; Δσsp4 = 0. Первые потери: Δσsp(1) = Δσsp1 + Δσsp2 +Δσsp3 +Δσsp4 = 146,4 кг/см2. Потери от усадки бетона: Δσsp5 = σb,sh·Es σb,sh – деформации усадки бетона, значение которого можно принять в зависимости от класса бетона (В30) равным: 0,0002 Δσsp5 = 0,0002·2·106 = 400 кг/см2. Потери от ползучести бетона Δσsp6 определяются по формуле: Δσsp6 = α = 6,29 φb,ser – коэффициент ползучести бетона. φb,ser = 2,3; σbpj - напряжение в бетоне на уровне центра тяжести рассматриваемой j-ой группы стержней напрягаемой арматуры; σbp = P(1)/Ared + (P(1) P(1) – усилие предварительного обжатия с учетом только первых потерь; еор – эксцентриситет усилия P(1) относительно центра тяжести приведенного сечения; µspj – коэффициент армирования, равный Aspj/A, где А – площадь поперечного сечения элемента; Аspj – площадь рассматриваемой группы стержней напрягаемой арматуры. P(1) = Asp(σsp – Δσsp(1)); σsp = 4880 кг/см2; Δσsp(1) = 146,4 кг/см2; Р(1) = 5,6(4880 – 146,4) = 26508,16 кг; еор = 7,8 см; Ired = 108296,23 108296,23 σbp = 26508,16/1792,12 + (26508,16·7,82)/ 108296,23 = 29,68 кг/см2; А = 1792,12 см2; µ = 5,6/1792,12 = 0,0031; Δσsp6 = Полное значение первых и вторых потерь: Δσsp(2) = Δσsp(2) = 146,4 + 400 + 211,51 = 757,91 кг/см2. При проектировании конструкций полные суммарные потери для арматуры расположенной в растянутой при эскплуатации зоне сечения элемента, следует принимать не менее 100 МПа (п. 2.2.3.9 СП 52-102-2004), поэтому принимаем Δσsp(2) = 1000 кг/см2. После того, как определены суммарные потери предварительного напряжения арматуры, можно определить Мcrc. Р(2) = (σsp – Δσsp(2))·Asp; P(2) – усилие предварительного обжатия с учетом полных потерь; Р(2) = (4880 – 1000)·5,6 = 21728 кг; Мcrc = Rbt,ser ·W + P(2)·eяр = 17,8·12534,3 + 21728 ·13,29 = 511875,7 кг·см = 5118,76 кг·м. Так как Mn = 3470,06 кг·м < Mcrc = 5118,76 кг·м, то трещины в растянутой зоне от эксплуатационных нагрузок не образуются.
Расчет прогиба плиты. Расчет изгибаемых элементов по прогибам производят из условия: ƒ ≤ ƒ ult, где ƒ – прогиб элемента от действия внешней нагрузки; ƒ ult – значение предельно допустимого прогиба. При действии постоянных, длительных и кратковременных нагрузок прогиб балок или плит во всех случаях не должен превышать 1/200 пролета. Для свободно опертой балки максимальный прогиб определяют по формуле: ƒ = Sl 2 (1/r) max, где S – коэффициент, зависящий от расчетной схемы и вида нагрузки; при действии равномерного рапределения нагрузки S = 5/48; при двух равных моментах по концам балки от силы обжатия – S = 1/8. (1/r)max – полная кривизна в сечении с наибольшим изгибающим моментов от нагрузки, при которой определяется прогиб. Полную кривизну изгибаемых элементов определяют для участков без трещин в растянутой зоне по формуле: 1/r = (1/r)1 + (1/r)2 - (1/r)3, где (1/r)1 – кривизна от непродолжительного действия кратковременных нагрузок; (1/r)2 – кривизна от продолжительного действия постоянных и длительных нагрузок; (1/r)3 – кривизна от непродолжительного действия усилия предварительного обжатия P(1), вычисленного с учетом только первых потерь, т.е. при действии момента М = Р(1)·е0р. Кривизну элемента на участке без трещин определяют по формуле: 1/r = M/(Eb1·Ired), где М – изгибающий момент от внешней нагрузки или момент усилия предварительного обжатия относительно оси, проходящей через центр тяжести приведенного сечения; Ired – момент инерции приведенного сечения; Eb1 – модуль деформации сжатого бетона, определяемый по формуле: Eb1 = Eb/(1+φb,cr), где φb,cr – коэффициент ползучести бетона Прогиб определяется с учетом эстетико-психологических требований, т.е. от действия только постоянных и временных длительных нагрузок: (1/r)2 = Mnl /(E b1·Ired) Eb1 = Eb/(1+φb,cr) = 331·103/(1+2,3) = 100303 кг/см3 (1/r)2 = Mnl/(Eb1·Ired) = 347006/(100303·108296,23) = 3,19·10-5 Кривизна от кратковременного выгиба при действии усилия предварительного обжатия (1/r)3 = (Р(1)·еор)/(Eb1·Ired) = (26508,16·7,8)/(100303 ·108296,23) = 1,9 ·10-5 В запас жесткости плиты оценим ее прогиб от постоянной и длительной нагрузок (без учета выгиба от усилия предварительного обжатия): ƒ = (5/48·3,19·10-5)·6092 = 1,23 см < 3,045 см; Допустимый прогиб ƒ = (1/200) l = 609/200 = 3,045 см. (1/r)4 – кривизна, обусловленная выгибом элемента вследствие усадки и ползучести бетона в стадии изготовления от неравномерного обжатия по высоте сечения плиты. (1/r)4 = (σsb – σ’sb)/(Es·h0), где σsb, σ’sb – значения, численно равные сумме потерь предварительного напряжения арматуры от усадки и ползучести бетона соотвественно для арматуры растянутой зоны и для арматуры, условно расположенной в уровне крайнего сжатого волокна бетона. σ’sb = Р(2)/Аred – (P(2)·eop·(h – y0))/Ired = = 21728/1827,34 – (21728 ·7,8·(22 – 10,8))/108296,23 = – 5,64 кг/см2. Следовательно, в верхнем волокне в стадии предварительного обжатия возникает растяжение, поэтому σ’sb = 0. Следует проверить, образуются ли в верхней зоне трещины в стадии предварительного обжатия: Мcrc = γ·
rinf – расстояние от центра тяжести приведенного сечения до ядровой точки, наиболее удаленной от грани элемента, растянутой усилием Р(1); Р(1) и e0p,1 – усилие обжатия с учетом первых потерь и его эксцентриситет относительно центра тяжести приведенного сечения;
γ = 1,25 – для двутаврового симметричного сечения; rinf = 9669,3/1827,34 = 5,29 см; e0p1 = 7,8 см; Р(1) = (σsp – Δσsp(1))·As; P(1) = (4880 – 146, 4)·5,6 = 26508,16 кг; Передаточная прочность назначается не менее 15 МПа и не менее 50% принятого класса бетона. Rbp = 224 кг/см2.
Mcrc = 1,25·9669,3·11,2 – 26508,16 · (7,8 – 5,29) = = 135370,2 – 66535,5 = 68834,7 кг·см = 688,3 кг·м > 0. Следовательно, трещины в верхней хоне в стадии предварительного обжатия не образуются. В нижней зоне в стадии эксплуатации трещин также нет. Для элементов без трещин сумма кривизн (1/r)3 + (1/r)4 принимается не менее кривизны от усилия предварительного обжатия при продолжительном его действии. При продолжительном действии усилия предварительного обжатия: Eb1 = 331·103/(1+2,3) = 10,03·104 кг/см2. (1/r)3 = (Р(2)·еор)/(Eb1·Ired) = (21728 ·7,8)/(100303·108296,23) = 1,56·10-5 σsb = Δσsb5 + Δσsb6; σsb = 400 + 211,51 = 611,51 кг/см2; (1/r)4 = 611,51 / (2·106·19) = 1,61·10-5 (1/r)3 + (1/r)4 = (1,9 + 1,61)·10-5 = 3,51·10-5 Это значение больше, чем кривизна от усилия предварительного обжатия при продолжительном его действии (1,56·10-5 Таким образом, прогиб плиты с учетом выгиба (в том числе его приращения равномерной усадки и ползучести бетона в стадии изготовления вследствие неравномерного обжатия сечения по высоте) будет равен: ƒ = (5/48·3,19·10-5 – 1/8·3,51·10-5)·6092 = – 0,395 см. 3. Вариант расчета многопустотной предварительно напряженной плиты перекрытия при действии временной нагрузки, равной 4,5 кН/м2.
Постоянная нагрузка та же, что при расчете плиты перекрытия на действие нагрузки V = 150 кг/м2.
Нагрузка на 1 погонный метр длины плиты при номинальной ее ширине 1,5 м: - расчетная постоянная g = 471,3·1,5·1 = 706,95 кг/м; - расчетная полная (g + V) = 1076,1·1,5·1 = 1614,15 кг/м; - нормативная постоянная gn = 415·1,5·1 = 622,2 кг/м; - нормативная полная (gn + Vn) = 919·1,5·1 = 1378,5 кг/м; - нормативная постоянная и длительная (gn + Vlon,n) = (415 + 214) ·1,5·1 = 943,6 кг/м.
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 3341; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.68.161 (0.008 с.) |

 (146·3,853)/12 + 146·3,85· (22 – 10,8 – 0,5·3,85)2 + (45,9·14,33)/12 + 45,9·14,3·(0,5·22 – 10,8)2 + (149·3,853)/12 + 149·3,85·(10,8 – 0,5·3,85)2 + 6,29·5,6·(10,8 – 3)2 = 694,3 + 48355,0 + 11185,1 + 26,3 + 708,6 + 45183,9 + 2143,03 =
(146·3,853)/12 + 146·3,85· (22 – 10,8 – 0,5·3,85)2 + (45,9·14,33)/12 + 45,9·14,3·(0,5·22 – 10,8)2 + (149·3,853)/12 + 149·3,85·(10,8 – 0,5·3,85)2 + 6,29·5,6·(10,8 – 3)2 = 694,3 + 48355,0 + 11185,1 + 26,3 + 708,6 + 45183,9 + 2143,03 = = Ired/(h – y0) = 108296,23/(22 – 10,8) = 9669,3 см3.
= Ired/(h – y0) = 108296,23/(22 – 10,8) = 9669,3 см3. , где
, где )/Ired;
)/Ired;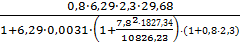 = 211,51 кг/см2.
= 211,51 кг/см2.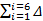 σspi
σspi .
.
 – P(1)(e0p,1 – rinf), где
– P(1)(e0p,1 – rinf), где – значение Rbt,ser при классе бетона, численно равном передаточной прочности Rbt;
– значение Rbt,ser при классе бетона, численно равном передаточной прочности Rbt;




