Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построением диаграммы Максвелла-КремоныСодержание книги
Поиск на нашем сайте
1. Определяют расчетные нагрузки на 1 м2 покрытия. Расчетная нагрузка равна произведению нормативной нагрузки на коэффициент перегрузки. Нормативную нагрузку, в свою очередь, определяют по правилам, приведенным в строительных нормах. Определение ее выходит за рамки задачи, поэтому нормативная постоянная gn и нормативная временная (снеговая) sn нагрузки приводят в условии задачи. Порядок определения расчетных нагрузок следующий. Расчетная постоянная нагрузки gd равна произведению нормативной нагрузки gn на коэффициент надежности по постоянно нагрузке gg:
Расчетная временная нагрузка sd равна произведению нормативной нагрузки sn на коэффициент надежности по временной нагрузке gs:
Полная нагрузка равна сумме постоянной и временной нагрузок. Полная нормативная нагрузка
Полная расчетная нагрузка
Все эти нагрузки являются распределенными на 1 м2 покрытия. 2. Определяют узловые нагрузки, т.е. нагрузки, приходящиеся на один узел фермы. Узловая нагрузка является сосредоточенной и равна произведению распределенной нагрузки на грузовую площадь, приходящуюся на этот узел.
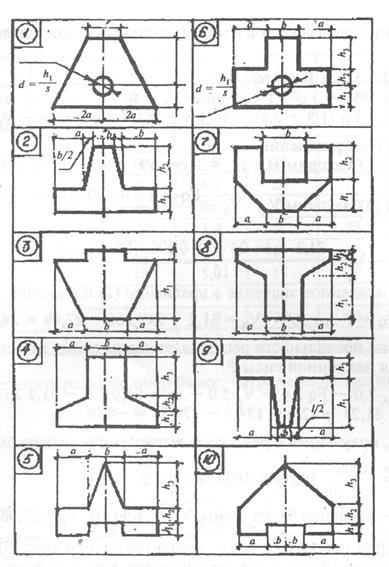
где qd - полная расчетная распределенная нагрузка на 1 м2 покрытия; Агруз – площадь покрытия, с которой собирается нагрузка на узел. Общая площадь в общем случае определяется по формуле
где b – шаг ферм или расстояние между смежными фермами; d - панель верхнего пояса фермы, или расстояние между серединами стержней пояса, примыкающих к узлу. Грузовые площади могут быть одинаковыми для всех промежуточных узлов или разными. Следовательно, узловые силы тоже могут быть одинаковыми или разными. 3. Вычерчивают геометрическую схему фермы строго в масштабе. Масштаб определяются размерами чертежа (1:300, 1:200, 1:100). После вычерчивания фермы к узлам прикладываются внешние силы. 4. Обозначают внешние и внутренние поля: а) внешние поля ограничены внешними силами и поясами фермы. Эти поля разомкнуты, их принято обозначать буквами а, b, c, d, …, обходя ферму по часовой стрелке. Первое поле, как правило, ограничено линией действия опорной реакции и первой (крайней) силы – оно представляет собой полуплоскость, расположенную слева от линии действия указанных сил. Если ферма и нагрузки имеют ось симметрии, то симметричные поля правой части фермы обозначаются теми же буквами, что и на левой части фермы обозначаются теми же буквами, что и на левой половине, но с индексами, например a’, b’, c’, d’, … Поле, расположенное между опорными реакциями, не имеет себе симметричного (при отсутствии нагрузки по нижнему поясу фермы);
б) внутренние поля ограничены только стержнями фермы. Они замкнуты, их обозначают цифрами 1, 2, 3, …, обходя ферму слева направо. При симметричной схеме фермы поля правой половины можно обозначать теми же цифрами, что и левой, например, 1’,2’, 3’, … 3. Определяют опорные реакции фермы графическим способом в следующем порядке: а) выбирают масштаб сил. Он также зависит от размеров чертежа; б) откладывают в принятом масштабе все внешние силы поочередно в том порядке, в каком они встречаются при обходе фермы по часовой стрелке. Теперь каждая сила будет обозначаться двумя полями (буквами), между которыми она расположена. Отложенные последовательно сверху вниз внешние силы образуют силовую линию, длина которой в масштабе сил равна сумме всех внешних сил, действующих на ферму; в) определяют опорные реакции фермы. Вследствие симметрии схемы фермы и нагрузки опорные реакции равны между собой, причем каждая из них составляет половину длины силовой линии и направлена вверх. Опорные реакции, как и внешние силы, обозначаются полями, между которыми они лежат. На силовую линию наносят точку, которая обозначает поле, расположенное между опорными реакциями. Она находится в середине силовой линии. Нижняя половина силовой линии является правой опорной реакцией, а верхняя – левой. 4. Строят собственно диаграмму усилий: а) обозначают стержни. При этом нужно твердо уяснить, что при графическом способе расчета каждый стержень обозначается двумя полями, между которыми он лежит. Наименование стержня зависит также от рассматриваемого узла: стержень обозначается двумя полями, которые читаются в том порядке, в каком встречаются при обходе рассматриваемого узла по часовой стрелке. Обозначение стержней может быть цифровым (1-2, 2-3 и т.д.) для элементов решетки и буквенно-цифровым (1-а, 2-в и т.д.) – для поясов и опорных стоек; б) мысленно вырезают узлы. Первым вырезают узел, в котором сходятся два стержня, - с чего начинается расчет. Стержни этого узла расположены между тремя полями: двумя буквенными и одним цифровым. На силовой линии уже есть точки, соответствующие буквенным полям. Через эти точки проводят линии, параллельные стержням рассматриваемого узла. Пересечение этих линий обозначаются цифрой, соответствующей цифре поля, примыкающего к рассматриваемому узлу. Стержень и параллельное ему усилие имеют одинаковое обозначение. Длина линии на диаграмме, измеренная в масштабе сил, и является величиной усилия в соответствующем стержне. Знак усилия определяется следующим образом. Сначала на схеме фермы читают название стержня, обходя узел по часовой стрелке, затем на диаграмме перемещаются по усилию от одной точки к другой в том порядке, как читается стержень, и, наконец, это движение переносят на стержень фермы. Если движение при этом направлено по стержню от узла, то стержень считается растянутым, а если у узлу – сжатым. На диаграмме сжатый стержень показывается жирной (или красной), а растянутый – тонкой (или синей) линией;
в) вырезают узел, в котором сходятся три стержня, причем усилия в двух из них неизвестны, а в третьем оно найдено при рассмотрении первого узла. На диаграмме усилий находят две точки, соответствующие двум полям, прилегающим к рассматриваемому узлу. Через эти точки проводят линии, параллельные стержням, усилия в которых неизвестны. Точку пересечения обозначают номером поля, которое лежит между двумя стержнями, усилия в которых отыскиваются. Длины линий на диаграмме, измеренные в масштабе сил, равны величине усилий в этих стержнях. Знак определяются по правилам, описанным для первого узла; г) каждым следующим рассматриваемым узлом будет тот, в котором сходятся два стержня с неизвестными усилиями, а усилия в остальных стержнях уже определены. Порядок определения величины и знака усилия остается тем же, что для первого и второго узлов. Для симметричной фермы диаграмму усилий можно строить для одной (левой) половины, усилия в стержнях правой половины равны усилиям в симметричных стержнях левой половины; д) определение усилий заканчивается составлением таблицы с обозначением стержней и указанием величины и знака усилий.
Пример 17. Определить усилия в стержнях от полной расчетной нагрузки на всей ферме путем построения диаграммы Максвелла-Кремоны, если qn =0,3кН/м2, sn =0,2кН/м2, gg =1,1, gs =1,4, шаг ферм b =6м (рис. 32, а). Решение. 1. Определим расчетную нагрузку на 1 м2: расчетная постоянная
Методические указания по выполнению контрольные вопросы
По данной дисциплине студентами выполняются две контрольные работы. Первая контрольная работы включает в себя выполнение пяти задач, вторая – двух. Все задачи составлены по многовариантной системе. Изучать дисциплину рекомендуется последовательно по темам, в соответствии с примерным тематическим планом и методическим указаниями к ним. Степень усвоения материала проверяется умением ответить на вопросы для самоконтроля, приведенные в конце каждой темы. Чтобы определить свой вариант контрольной работы студенту необходимо воспользоваться таблицей, приведенной к каждой задаче, которая построена следующим образом: - вертикальная крайняя графа содержит алфавит, - в вертикальной графе 1 указаны схемы к задаче,
- остальные вертикальные графы содержат числовые данные, необходимые для решения задачи. Контрольная работа, выполненная не в соответствии с этими данными, не засчитывается и возвращается студенту. При выполнении контрольной работы необходимо соблюдать следующие требования: - записываются условия задач; - решения задач следует сопровождать пояснениями; - вычислениям должны предшествовать исходные формулы; - для всех исходных и вычисленных физических величин должны указываться размерности; - приводятся необходимые эскизы и схемы. В установленные учебным графиком сроки студент стает работу на проверку. Незачетные контрольные работы подлежат повторному выполнению В методических указаниях к выполнению практических работ приведены примеры решения задач.
ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ № 1 Задача № 1. Определить аналитическим и графическим способами усилия в стержнях АВ и ВС заданной стержней системы (рис. 28). Исходные данные для задачи своего варианта взять из таблицы 1 (графы 1, 4 – начальная буква фамилии, 2, 5 – имени, 3, 6 – отчества).
Таблица 1.
Рис. 28 Задача № 2. Определить реакции опор балки, нагруженной, как показано на рис. 29. Исходные данные приведены в таблице 2.
Таблица 2.
Рис. 29
Задача № 3. Для сечения сборных элементов зданий (рис. 30) определить положение центра тяжести. Данные для задачи своего варианта взять из таблицы 3.
Таблица 3.
Рис. 30
Задача № 4. Для двухопорной балки (рис. 31) построить эпюры изгибающих моментов и поперечных сил, подобрать сечение стального двутавра. Расчет провести по допускаемым напряжениям, приняв [s]=160МПа. Данные для задачи своего варианта взять из таблицы 4.
Таблица 4.
Рис. 31
Задача № 5. По оси ступенчатого бруса приложены силы F1 и F2. Необходимо построить эпюры продольных сил и нормальных напряжений, определить абсолютную деформацию бруса (рис. 32). Принять Е=2,1·105 МПа. Данные для задачи своего варианта взять из таблицы 5.
Таблица 5.
Рис. 32
Пример 15. Для данного ступенчатого бруса (рис. 33) построить эпюры продольных сил и нормальных напряжений. Определить абсолютное удлинение (укорочение) бруса. Дано: F1=28 кН; F2=64 кН; l1= 2,4 м; l2= 2,2 м; l3= 2,0 м; А=3,2см2; Е=2,1·105 МПа.
Рис. 33
Решение. 1. Проводим ось Z в сторону свободного конца бруса и определяем реакцию заделки V.
2. Разбиваем брус на участки, границы которых определяются сечениям, где изменяется площадь поперечного сечения или приложены внешние силы. На каждом из участков проводим характерные сечения 1-1, 2-2, 3-3. С помощью метода сечений определяем продольные силы на каждом из участков бруса: мысленно рассекаем брус в пределах первого участка сечением 1-1, отбрасываем верхнюю часть бруса и заменяем ее действие продольной силой N1, для оставшейся части составляем уравнение равновесия:
Аналогично находим N2 и N3: сечение 2-2
сечение 3-3
По найденным значениям продольной силы строим соответствующую эпюру. Для этого параллельно оси бруса проведем базовую (нулевую) линию. Левее ее откладываем отрицательные значения N, соответствующие сжатому участку, а правее – положительные, соответствующие растянутому участку. Определяем нормальные напряжения в характерных сечениях бруса по формуле
Строим соответствующую найденным значениям эпюру σ. Определяем абсолютное удлинение бруса. В соответствии с законом Гука:
где Е=2,1·105 МПа – модуль продольной упругости для стали.
Складывая удлинение участков, получим:
Учитывая, что 1м=103мм будем иметь
Абсолютное удлинение бруса
ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ № 2 Задача № 1. Для заданной статически определимой фермы (рис. 34) необходимо построить диаграмму Максвелла-Кремоны; по построенной диаграмме определить числовые значения усилий и составить таблицу расчетных усилий. Данные для задачи своего варианта взят из таблицы 6.
Таблица 6.
Рис. 34
Задача № 2. Построить эпюры Q и M для неразрезной балки (рис. 35). Данные для задачи своего варианта взять из таблицы 7.
Таблица 7.
Рис. 35 VI. приложение
Приложение 1 Таблица 1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 2145; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.195.78 (0.013 с.) |




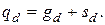
 ,
,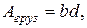












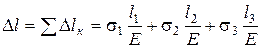 или
или