
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение эпюр поперечных сил и изгибающихСодержание книги
Поиск на нашем сайте
Моментов для балки на двух опорах Пример 11. Построить эпюры Qx и Мx балки, показанной на рис. 19, а. Решение. 1. Определим опорные реакции балки. Составим уравнения: 1) Из первого уравнения найдем VB:
или
откуда Из второго уравнения найдем VА:
или
откуда Выполним проверку:
или
2. Обозначим характерные сечения балки C, D, A, E, B. K. 3. Строим эпюру Qx. Определим значения поперечных сил в характерных сечениях:
Соединим полученные значения прямыми линиями (рис. 19, б) и получим эпюру Qx. Эпюра Qx на участке АЕ пересекает нулевую линию. Определим положение точки, в которой эпюра Qx пересекает нулевую линию. Рассмотрим подобие треугольников HRL и HNS (см. рис. 19, б), откуда HR/HN = HL/HS, или x0/5 = 73,6/100, откуда
Это сечение считается также характерным для эпюры Qx и Мx.
Рис. 19
4. Строим эпюру Мx (см. рис. 19, в). Определим изгибающие моменты в характерных точках:
5. Проверка. В качестве проверки возьмем сумму моментов всех сил относительно точки, расположенной на расстоянии x0 от левой опоры, но рассмотрим правую часть балки:
Разница в значениях Мx при рассмотрении левых и правых сил возможна из-за округления величин опорных реакций и расстояния x0.
Задание для практической работы № 10. Построить эпюры Qx и Мx балки по данным одного из вариантов, показанных на рис. 20.
Рис. 20
Рис. 20 Продолжение
Рис. 20 Продолжение
Рис. 20 Окончание
Практическая работа № 11 Определение допустимого значения центрально-сжимающей силы 1. Определяют величину расчетного сопротивления материала на сжатие R, как правило, по справочникам или строительным нормам. Для решения можно воспользоваться прил. VIII. 2. Находят площадь поперечного сечения А стойки. 3. Определяют коэффициент продольного изгиба j в следующем порядке: а) вначале определяют расчетную (эффективную) длину стержня
где µ - коэффициент приведения длины, который зависит от способа закрепления концов стержня (см. прил. III); l – геометрическая длина стержня; б) потом определяют моменты инерции сечения Jx и Jy относительно главных центральных осей. Формулы для определения моментов инерции простых геометрических фигур относительно собственных осей приведены в прил. II. Моменты инерции профилей проката приведены в ГОСТах (см. прил. I);
в) находят радиусы инерции сечения относительно осей x и y:
Если ix и iy не равны между собой, то для дальнейших расчетов принимают наименьший из них, обозначив его imin. Если ix = iy, то расчет можно вести по любому из них; г) определяют гибкость стержня:
д) по найденному значению гибкости в зависимости от материала стержня определяют коэффициент продольного изгиба (см. прил. IV). При этом, как правило, приходиться пользоваться интерполяцией. 4. Определяют величину допускаемого значения сжимающей силы:
Пример 12. Определить значение допустимой силы для центрально-сжатого стержня, показанного на рис. 21, а. Материал стержня сталь марки С-245. Сечение стержня состоит из четырех уголков 100х63х8. Решение. 1. Расчетное сопротивление стали R = 240 МПа (прил. VIII) 2. Площадь поперечного сечения стержня (рис. 21, б)
3. Определить коэффициент продольного изгиба j: а) расчетная длина стержня
Рис. 21
где µ=1 (прил. III); б) определим моменты инерции сечения относительно осей x и y. Поскольку сечение состоит из неравнополочных уголков, то момент инерции относительно оси x не будет равен моменту инерции относительно оси y. Момент инерции относительно оси y
где Момент инерции относительно оси x
где Момент инерции относительно оси x является наименьшим; в) минимальный радиус инерции сечения
г) наибольшая гибкость стержня
д) коэффициент j определим по прил. IV, интерполируя значения гибкости l=70 (j=0,754) и l=80 (j=0,686):
4. Допустимая сжимающая сила
Задание для практической работы № 11. Определить величину допускаемого значения центрально-сжимающей силы по данным одного из вариантов, показанных на рис. 22. Для нечетных вариантов материал для стержня – алюминий марки АМг2М, для четных – сталь марки С-345.
Рис. 22
Рис. 22 Продолжение
Рис. 22 Продолжение
Рис. 22 Окончание
Практическая работа № 12
|
|||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 2380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.42.159 (0.01 с.) |

 2)
2) 

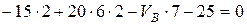 ,
,
 .
.
 ,
, .
.
 откуда
откуда  .
.











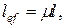



 (см. табл. 1, прил.I).
(см. табл. 1, прил.I).


 , принято по табл. 1 и 2, прил. I.
, принято по табл. 1 и 2, прил. I.
 принято по табл. 1 и 2, прил. I.
принято по табл. 1 и 2, прил. I.













