
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематический анализ кулачковых механизмовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задачей кинематического анализа кулачкового механизма так же, как и других механизмов, является определение в нём закона преобразования движения с одновременным определением скоростей и ускорений толкателя при заданной скорости вращения кулачка (в случае вращающегося кулачка). При этом чаще всего принимается, что угловая скорость кулачка В результате анализа кинематики определяется функция положения механизма в форме Из этих простейших выкладок ясно, что анализ кинематики необходимо начинать с определения функции положения, то есть зависимости перемещения толкателя от угла поворота кулачка. Рассмотрим несколько методов решения этой задачи.
Кулачок 1 вращается против часовой стрелки с угловой скоростью
Это и есть функция положения механизма. Продифференцировав один раз полученное выражение, находим аналог скорости
После второго дифференцирования получаем аналог ускорения
Г р а ф и ч е с к и й м е т о д с и с п о л ь з о в а н и е м г р а ф и ч е с- Решение задачи начинается с разборки механизма и очерчивания рабочего профиля его кулачка на листе бумаги (рис. 9.6). Центр кулачка определяется известным геометрическим способом. Затем из этого центра проводится окружность эксцентриситета и основная окружность рабочего профиля. С помощью радиуса ролика производится переход от рабочего профиля к теоретическому. Для этого раствором циркуля, равным радиусу ролика, проводится ряд окружностей (или дуг окружностей) с центрами на линии рабочего профиля. Огибающая этих окружностей даст теоретический профиль. Ось толкателя во всех положениях механизма остаётся касательной к окружности эксцентриситета, поэтому через небольшой угловой интервал необходимо провести как можно больше касательных к этой окружности с той стороны от центра кулачка, с которой располагается толкатель. Касательные необходимо пронумеровать в направлении, обратном направлению вращения кулачка. На этих касательных расстояния между точками их пересечения с основной окружностью теоретического профиля радиуса
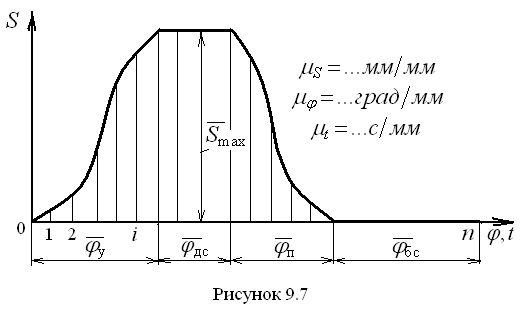
После измерения во всех положениях механизма перемещения толкателя представляются в виде графика По оси абсцисс вместо угла поворота
Сумма углов удаления, дальнего стояния и приближения образует так называемый рабочий угол Для построения графика аналога скорости необходимо продифференцировать полученный график функции положения по П л а н с к о р о с т е й к у л а ч к о в о г о м е х а н и з м а. Для анализа кинематики кулачкового механизма полезно уметь построить для него план скоростей. Возьмём кулачковый механизм с поступательно движущимся толкателем (рис. 9.8, а). Для простоты будем считать, что заранее нами построен теоретический профиль. В этом случае с ним в контакте работает толкатель, оканчивающийся остриём.
Обозначим Г р а ф и ч е с к и й м е т о д с и с п о л ь з о в а н и е м о с н о в н о г о
Проведём нормаль n – n к профилям в точке K, которая пройдёт через центр ролика и пересечёт межосевую линию в полюсе зацепления П. Так как полюс зацепления П является точкой касания центроид, то скорости точек, принадлежащих центроидам звеньев, одинаковы. Толкатель совершает поступательное движение, поэтому скорости всех его точек равны друг другу и скорости полюса. Значит, для определения скорости толкателя необходимо знать скорость полюса, а она найдётся по формуле Так можно определить скорость полюса, а следовательно, и скорость толкателя во всех требуемых положениях механизма и далее поступить с ней так же, как это пояснялось выше.
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 1027; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.195.180 (0.007 с.) |

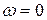 .
. и её производные по
и её производные по 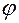 :
:  , называемая аналогом скорости, и
, называемая аналогом скорости, и 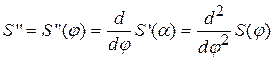 , называемая аналогом ускорения. Аналогичным образом определяются данные кинематические параметры и в случае возвратно-вращательного движения толкателя. Как известно из материалов по исследованию кинематики рычажных механизмов, имея аналоги скоростей и ускорений, легко вычислить и сами скорости и ускорения толкателя, то есть
, называемая аналогом ускорения. Аналогичным образом определяются данные кинематические параметры и в случае возвратно-вращательного движения толкателя. Как известно из материалов по исследованию кинематики рычажных механизмов, имея аналоги скоростей и ускорений, легко вычислить и сами скорости и ускорения толкателя, то есть  и
и  .
. А н а л и т и ч е с к и й м е т о д. Возьмём для простоты тангенциальный кулачок, профиль которого на некотором участке очерчен прямой линией
А н а л и т и ч е с к и й м е т о д. Возьмём для простоты тангенциальный кулачок, профиль которого на некотором участке очерчен прямой линией 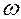 вокруг точки O. Отсчёт угла поворота
вокруг точки O. Отсчёт угла поворота 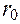 . Это расстояние определяется разностью
. Это расстояние определяется разностью  . Так как из прямоугольного треугольника OA 0 A
. Так как из прямоугольного треугольника OA 0 A  , то
, то .
. .
.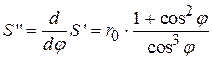 .
.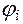 , и соответствующее ему перемещение отмечено
, и соответствующее ему перемещение отмечено  .
.
 (рис. 9.7).
(рис. 9.7). , имея в виду линейную зависимость между углом поворота кулачка и временем, а именно,
, имея в виду линейную зависимость между углом поворота кулачка и временем, а именно,  . Согласно этой зависимости шкала времени будет равномерной, как и угловая шкала. В точке
. Согласно этой зависимости шкала времени будет равномерной, как и угловая шкала. В точке  на рисунке будет заканчиваться время полного оборота кулачка
на рисунке будет заканчиваться время полного оборота кулачка  .
.
 . Поделив рабочий угол на угловую скорость кулачка, получим время прохождения механизмом рабочего угла, то есть
. Поделив рабочий угол на угловую скорость кулачка, получим время прохождения механизмом рабочего угла, то есть  .
.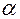 . Повторное дифференцирование даёт график аналога ускорения. Если вместо
. Повторное дифференцирование даёт график аналога ускорения. Если вместо 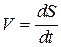 . Затем продифференцировав график скорости также по времени согласно формуле
. Затем продифференцировав график скорости также по времени согласно формуле  , построится график ускорения. Методика графического дифференцирования изложена в разделе кинематики механизмов с низшими кинематическими парами.
, построится график ускорения. Методика графического дифференцирования изложена в разделе кинематики механизмов с низшими кинематическими парами.
 точку кулачка 1, находящуюся в данный момент в контакте с толкателем 2, и
точку кулачка 1, находящуюся в данный момент в контакте с толкателем 2, и 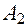 точку толкателя, контактирующую с кулачком. В данный момент эти точки совпадают друг с другом. Векторное уравнение скоростей для точек
точку толкателя, контактирующую с кулачком. В данный момент эти точки совпадают друг с другом. Векторное уравнение скоростей для точек  .
.  и направленной перпендикулярно R в сторону вращения кулачка, то есть известной по величине и направлению. Второе слагаемое представляет относительную скорость точки
и направленной перпендикулярно R в сторону вращения кулачка, то есть известной по величине и направлению. Второе слагаемое представляет относительную скорость точки  з а к о н а з а ц е п л е н и я. Вместо метода планов скоростей можно для определения скоростей воспользоваться основным законом зацепления. Пусть имеется кулачковый механизм с поступательно движущимся роликовым толкателем (рис. 9.9). С точки зрения теории зацепления центры вращения звеньев, образующих высшую пару, лежат на так называемой межосевой линии. Причём, в данном случае центр O кулачка находится в пределах чертежа, а центр вращения толкателя находится в бесконечности, так как толкатель движется поступательно. Поэтому межосевая линия расположена горизонтально и образует прямой угол с осью толкателя. Ролик толкателя и кулачок находятся в котакте между собой в точке K.
з а к о н а з а ц е п л е н и я. Вместо метода планов скоростей можно для определения скоростей воспользоваться основным законом зацепления. Пусть имеется кулачковый механизм с поступательно движущимся роликовым толкателем (рис. 9.9). С точки зрения теории зацепления центры вращения звеньев, образующих высшую пару, лежат на так называемой межосевой линии. Причём, в данном случае центр O кулачка находится в пределах чертежа, а центр вращения толкателя находится в бесконечности, так как толкатель движется поступательно. Поэтому межосевая линия расположена горизонтально и образует прямой угол с осью толкателя. Ролик толкателя и кулачок находятся в котакте между собой в точке K. , так как кулачок вращается вокруг центра O вместе со своей центроидой.
, так как кулачок вращается вокруг центра O вместе со своей центроидой.


