

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Трение в поступательной кинематической паре
У г о л и к о н у с т р е н и я. Угол, образованный полной реакцией в поступательной паре и её нормальной составляющей, называется углом трения. Ползун находится на плоскости и движется по ней со скоростью 
(рис. 5.5). На ползун сверху вниз действует сила Q, вызывающая появление нормальной реакции N. Навстречу движению ползуна на его нижней плоскости действует сила трения 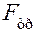 против относительной скорости. Геометрическая сумма нормальной составляющей реакции и силы трения равна полной реакции R в кинематической паре ползуна с плоскостью. Угол против относительной скорости. Геометрическая сумма нормальной составляющей реакции и силы трения равна полной реакции R в кинематической паре ползуна с плоскостью. Угол 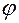 между этой реакцией и её нормальной составляющей N и является углом трения. Величина угла трения определяется следующей формулой, которая очевидна из рисунка, между этой реакцией и её нормальной составляющей N и является углом трения. Величина угла трения определяется следующей формулой, которая очевидна из рисунка,  , или , или 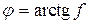 (причём, (причём,  ), то есть угол трения – это угол, тангенс которого равен коэффициенту трения. Если двигать ползун в различных направлениях, то полная реакция опишет коническую поверхность, которая называется конусом трения. В общем случае конус трения не является круглым, так как условия трения в разных направлениях могут быть различными и сила трения может быть также различной. Значение угла и конуса трения заключается в том, что если движущая сила своей линией действия проходит внутри конуса трения (угла трения), то движение под действием этой силы невозможно. Для доказательства этого положения обратимся к рис. 5.6. На нём показан ползун, движущийся вправо со скоростью V. Сила ), то есть угол трения – это угол, тангенс которого равен коэффициенту трения. Если двигать ползун в различных направлениях, то полная реакция опишет коническую поверхность, которая называется конусом трения. В общем случае конус трения не является круглым, так как условия трения в разных направлениях могут быть различными и сила трения может быть также различной. Значение угла и конуса трения заключается в том, что если движущая сила своей линией действия проходит внутри конуса трения (угла трения), то движение под действием этой силы невозможно. Для доказательства этого положения обратимся к рис. 5.6. На нём показан ползун, движущийся вправо со скоростью V. Сила 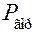 , вызывающая движение в этом направлении, является горизонтальной составляющей силы P, то есть , вызывающая движение в этом направлении, является горизонтальной составляющей силы P, то есть  , где , где  – угол между вертикалью и линией действия силы P. Этому движению препятствует сила трения – угол между вертикалью и линией действия силы P. Этому движению препятствует сила трения 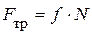 , где из условия равновесия , где из условия равновесия  , вертикальной составляющей силы P. Так как , вертикальной составляющей силы P. Так как  , то сила трения , то сила трения  . .
Возможны следующие три случая:
1.  , то есть , то есть  = =  , или , или 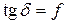 . Так как . Так как  , то получаем , то получаем  . Это значит, что при равенстве угла наклона движущей силы и угла трения будет сохраняться равномерное движение или состояние покоя. . Это значит, что при равенстве угла наклона движущей силы и угла трения будет сохраняться равномерное движение или состояние покоя.
2.  . Согласно приведённым выше выкладкам, получим . Согласно приведённым выше выкладкам, получим 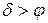 , в этом случае будет происходить движение с ускорением, так как движущая сила больше силы сопротивления. , в этом случае будет происходить движение с ускорением, так как движущая сила больше силы сопротивления.
3.  . Здесь получается соотношение, обратное предыдущему, то есть . Здесь получается соотношение, обратное предыдущему, то есть  , при котором движение будет невозможным, какую бы силу ни удалось приложить в направлении движения. , при котором движение будет невозможным, какую бы силу ни удалось приложить в направлении движения.
Т р е н и е н а н а к л о н н о й п л о с к о с т и. Рассмотрим ползун, находящийся на наклонной плоскости, образующей угол 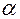 с горизонтом (рис. 5.7, а). Ползун движется вверх по наклонной плоскости со скоростью с горизонтом (рис. 5.7, а). Ползун движется вверх по наклонной плоскости со скоростью  под действием движущей силы P, направленной под углом под действием движущей силы P, направленной под углом  к плоскости. На ползун действует также сила Q под углом к плоскости. На ползун действует также сила Q под углом 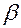 к вертикали, прижимая ползун к плоскости. И, наконец, на ползун также действует реакция к вертикали, прижимая ползун к плоскости. И, наконец, на ползун также действует реакция 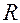 наклонной плоскости, отклонённая от нормали к ней на угол трения наклонной плоскости, отклонённая от нормали к ней на угол трения 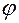 . .
Известными величинами здесь являются сила Q, угол 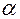 и коэффициент трения f, следовательно, угол и коэффициент трения f, следовательно, угол 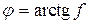 . Задача заключается в определении движущей силы P, необходимой для движения ползуна. Она решается с помощью сил, действующих на ползун, согласно уравнению . Задача заключается в определении движущей силы P, необходимой для движения ползуна. Она решается с помощью сил, действующих на ползун, согласно уравнению 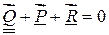 , в котором первый вектор подчёркнут дважды, так как он задан, два другие подчеркнуты одной чертой, так как они известны только по направлению. , в котором первый вектор подчёркнут дважды, так как он задан, два другие подчеркнуты одной чертой, так как они известны только по направлению.

Построив треугольник сил (план сил) (рис. 5.7, б), приступаем к его решению. Удобнее всего здесь воспользоваться теоремой синусов, согласно которой в косоугольном треугольнике отношение сторон к синусу противолежащего угла является постоянной величиной (необходимые для решения углы указаны на плане сил)
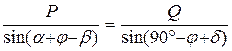 . .
Знаменатель правой части может быть заменён на  . Решая после этого данное выражение относительно P, получаем . Решая после этого данное выражение относительно P, получаем
 . .
Частные случаи.
1. Сила Q действует вертикально вниз, тогда  , и выражение приобретает вид , и выражение приобретает вид
 . .
2. Сила Q действует вертикально вниз, сила P горизонтальна, то есть угол  , ,  , тогда , тогда
 . .
 Самотормозящаяся наклонная плоскость. Самотормозящаяся наклонная плоскость.
Наклонная плоскость называется самотормозящейся, если движение по ней вниз под действием силы тяжести невозможно. Предельным случаем самотормозящейся наклонной плоскости является горизонтальная плоскость, у которой угол наклона  . Однако движение под действием силы тяжести становится невозможным и при некотором значении α, не равном нулю. Рассмотрим ползун на наклонной плоскости (рис. 5.8), на который вертикально вниз действует сила тяжести . Однако движение под действием силы тяжести становится невозможным и при некотором значении α, не равном нулю. Рассмотрим ползун на наклонной плоскости (рис. 5.8), на который вертикально вниз действует сила тяжести  . При скольжении ползуна вниз сила трения . При скольжении ползуна вниз сила трения 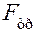 направлена вверх по наклонной плоскости, а полная реакция направлена вверх по наклонной плоскости, а полная реакция 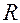 отклонена от нормали n-n на угол трения отклонена от нормали n-n на угол трения 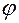 . Составляющая . Составляющая 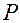 силы веса силы веса  , направленная вниз по наклонной плоскости, является движущей силой и составляет величину , направленная вниз по наклонной плоскости, является движущей силой и составляет величину  , а так как , а так как  , то , то  . Силу трения создаёт нормальная составляющая . Силу трения создаёт нормальная составляющая 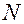 полной реакции полной реакции 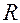 , причём эта составляющая равна нормальной составляющей силы веса, т. е. , причём эта составляющая равна нормальной составляющей силы веса, т. е.  . Сила трения равна . Сила трения равна  . Если сила . Если сила 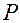 меньше силы трения меньше силы трения 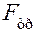 , то движение вниз невозможно. С учётом имеющихся выражений сил запишем это условие так: , то движение вниз невозможно. С учётом имеющихся выражений сил запишем это условие так:  , или , или  . Так как . Так как  , то получаем , то получаем  , или , или  . Это и есть условие самоторможения наклонной плоскости – угол наклона плоскости должен быть меньше угла трения. . Это и есть условие самоторможения наклонной плоскости – угол наклона плоскости должен быть меньше угла трения.
Т р е н и е к л и н ч а т о г о п о л з у н а. Клинчатый ползун часто применяется в виде направляющих металлорежущих станков и другого оборудования, где требуется перемещать вдоль направляющих некоторые устройства, например суппорт станка и др.
 На рис. 5.9, а изображена схема клинчатого ползуна в двух проекциях. На него действует сверху вниз сила Q, которая на боковых наклонных стенках жёлоба вызывает появление нормальных реакций N, а от них затем появляется сила трения На рис. 5.9, а изображена схема клинчатого ползуна в двух проекциях. На него действует сверху вниз сила Q, которая на боковых наклонных стенках жёлоба вызывает появление нормальных реакций N, а от них затем появляется сила трения 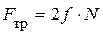 . Известными являются сила Q и коэффициент трения . Известными являются сила Q и коэффициент трения 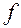 . Требуется определить движущую силу P, приводящую в движение ползун в направлении скорости V. Из плана сил ползуна, который построен по уравнению равновесия . Требуется определить движущую силу P, приводящую в движение ползун в направлении скорости V. Из плана сил ползуна, который построен по уравнению равновесия  (рис. 5.9, б), можем определить нормальные составляющие (рис. 5.9, б), можем определить нормальные составляющие 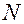 . Здесь мы имеем в виду, что, вследствие симметричности ползуна, модули нормальных реакций справа и слева равны друг другу, и поэтому на плане сил они обозначены одинаково. Итак, . Здесь мы имеем в виду, что, вследствие симметричности ползуна, модули нормальных реакций справа и слева равны друг другу, и поэтому на плане сил они обозначены одинаково. Итак,  . Отсюда следует, что . Отсюда следует, что  . Так как движущая сила . Так как движущая сила  , то , то  . Отношение . Отношение  зависит от условий трения в контакте ползуна с направляющими и от геометрии зоны контакта. Он называется приведённым коэффициентом трения клинчатого ползуна и обозначается зависит от условий трения в контакте ползуна с направляющими и от геометрии зоны контакта. Он называется приведённым коэффициентом трения клинчатого ползуна и обозначается  , то есть , то есть  , а движущая сила , а движущая сила 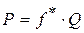 . .
На горизонтальной плоскости угол 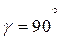 , поэтому , поэтому 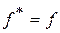 . .
Потери мощности на трение в поступательной кинематической паре определяются формулой  , причём сила трения вычисляется через реакцию в паре, которую мы научились определять выше в силовом расчёте групп Ассура. , причём сила трения вычисляется через реакцию в паре, которую мы научились определять выше в силовом расчёте групп Ассура.
|





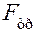 против относительной скорости. Геометрическая сумма нормальной составляющей реакции и силы трения равна полной реакции R в кинематической паре ползуна с плоскостью. Угол
против относительной скорости. Геометрическая сумма нормальной составляющей реакции и силы трения равна полной реакции R в кинематической паре ползуна с плоскостью. Угол 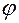 между этой реакцией и её нормальной составляющей N и является углом трения. Величина угла трения определяется следующей формулой, которая очевидна из рисунка,
между этой реакцией и её нормальной составляющей N и является углом трения. Величина угла трения определяется следующей формулой, которая очевидна из рисунка,  , или
, или 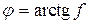 (причём,
(причём,  ), то есть угол трения – это угол, тангенс которого равен коэффициенту трения. Если двигать ползун в различных направлениях, то полная реакция опишет коническую поверхность, которая называется конусом трения. В общем случае конус трения не является круглым, так как условия трения в разных направлениях могут быть различными и сила трения может быть также различной. Значение угла и конуса трения заключается в том, что если движущая сила своей линией действия проходит внутри конуса трения (угла трения), то движение под действием этой силы невозможно. Для доказательства этого положения обратимся к рис. 5.6. На нём показан ползун, движущийся вправо со скоростью V. Сила
), то есть угол трения – это угол, тангенс которого равен коэффициенту трения. Если двигать ползун в различных направлениях, то полная реакция опишет коническую поверхность, которая называется конусом трения. В общем случае конус трения не является круглым, так как условия трения в разных направлениях могут быть различными и сила трения может быть также различной. Значение угла и конуса трения заключается в том, что если движущая сила своей линией действия проходит внутри конуса трения (угла трения), то движение под действием этой силы невозможно. Для доказательства этого положения обратимся к рис. 5.6. На нём показан ползун, движущийся вправо со скоростью V. Сила 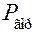 , вызывающая движение в этом направлении, является горизонтальной составляющей силы P, то есть
, вызывающая движение в этом направлении, является горизонтальной составляющей силы P, то есть  , где
, где  – угол между вертикалью и линией действия силы P. Этому движению препятствует сила трения
– угол между вертикалью и линией действия силы P. Этому движению препятствует сила трения 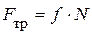 , где из условия равновесия
, где из условия равновесия  , вертикальной составляющей силы P. Так как
, вертикальной составляющей силы P. Так как  , то сила трения
, то сила трения  .
. , то есть
, то есть  =
=  , или
, или 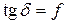 . Так как
. Так как  , то получаем
, то получаем  . Это значит, что при равенстве угла наклона движущей силы и угла трения будет сохраняться равномерное движение или состояние покоя.
. Это значит, что при равенстве угла наклона движущей силы и угла трения будет сохраняться равномерное движение или состояние покоя. . Согласно приведённым выше выкладкам, получим
. Согласно приведённым выше выкладкам, получим 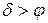 , в этом случае будет происходить движение с ускорением, так как движущая сила больше силы сопротивления.
, в этом случае будет происходить движение с ускорением, так как движущая сила больше силы сопротивления. . Здесь получается соотношение, обратное предыдущему, то есть
. Здесь получается соотношение, обратное предыдущему, то есть  , при котором движение будет невозможным, какую бы силу ни удалось приложить в направлении движения.
, при котором движение будет невозможным, какую бы силу ни удалось приложить в направлении движения.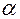 с горизонтом (рис. 5.7, а). Ползун движется вверх по наклонной плоскости со скоростью
с горизонтом (рис. 5.7, а). Ползун движется вверх по наклонной плоскости со скоростью  под действием движущей силы P, направленной под углом
под действием движущей силы P, направленной под углом 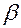 к вертикали, прижимая ползун к плоскости. И, наконец, на ползун также действует реакция
к вертикали, прижимая ползун к плоскости. И, наконец, на ползун также действует реакция 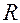 наклонной плоскости, отклонённая от нормали к ней на угол трения
наклонной плоскости, отклонённая от нормали к ней на угол трения 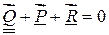 , в котором первый вектор подчёркнут дважды, так как он задан, два другие подчеркнуты одной чертой, так как они известны только по направлению.
, в котором первый вектор подчёркнут дважды, так как он задан, два другие подчеркнуты одной чертой, так как они известны только по направлению.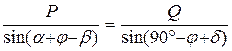 .
. . Решая после этого данное выражение относительно P, получаем
. Решая после этого данное выражение относительно P, получаем .
. , и выражение приобретает вид
, и выражение приобретает вид .
. , тогда
, тогда .
. Самотормозящаяся наклонная плоскость.
Самотормозящаяся наклонная плоскость. . Однако движение под действием силы тяжести становится невозможным и при некотором значении α, не равном нулю. Рассмотрим ползун на наклонной плоскости (рис. 5.8), на который вертикально вниз действует сила тяжести
. Однако движение под действием силы тяжести становится невозможным и при некотором значении α, не равном нулю. Рассмотрим ползун на наклонной плоскости (рис. 5.8), на который вертикально вниз действует сила тяжести  . При скольжении ползуна вниз сила трения
. При скольжении ползуна вниз сила трения 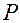 силы веса
силы веса  , а так как
, а так как  , то
, то  . Силу трения создаёт нормальная составляющая
. Силу трения создаёт нормальная составляющая 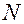 полной реакции
полной реакции  . Сила трения равна
. Сила трения равна  . Если сила
. Если сила  , или
, или  . Так как
. Так как  , или
, или  . Это и есть условие самоторможения наклонной плоскости – угол наклона плоскости должен быть меньше угла трения.
. Это и есть условие самоторможения наклонной плоскости – угол наклона плоскости должен быть меньше угла трения. На рис. 5.9, а изображена схема клинчатого ползуна в двух проекциях. На него действует сверху вниз сила Q, которая на боковых наклонных стенках жёлоба вызывает появление нормальных реакций N, а от них затем появляется сила трения
На рис. 5.9, а изображена схема клинчатого ползуна в двух проекциях. На него действует сверху вниз сила Q, которая на боковых наклонных стенках жёлоба вызывает появление нормальных реакций N, а от них затем появляется сила трения 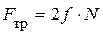 . Известными являются сила Q и коэффициент трения
. Известными являются сила Q и коэффициент трения 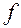 . Требуется определить движущую силу P, приводящую в движение ползун в направлении скорости V. Из плана сил ползуна, который построен по уравнению равновесия
. Требуется определить движущую силу P, приводящую в движение ползун в направлении скорости V. Из плана сил ползуна, который построен по уравнению равновесия  (рис. 5.9, б), можем определить нормальные составляющие
(рис. 5.9, б), можем определить нормальные составляющие  . Отсюда следует, что
. Отсюда следует, что  . Так как движущая сила
. Так как движущая сила  , то
, то  . Отношение
. Отношение  зависит от условий трения в контакте ползуна с направляющими и от геометрии зоны контакта. Он называется приведённым коэффициентом трения клинчатого ползуна и обозначается
зависит от условий трения в контакте ползуна с направляющими и от геометрии зоны контакта. Он называется приведённым коэффициентом трения клинчатого ползуна и обозначается  , то есть
, то есть  , а движущая сила
, а движущая сила 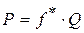 .
.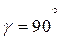 , поэтому
, поэтому 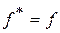 .
. , причём сила трения вычисляется через реакцию в паре, которую мы научились определять выше в силовом расчёте групп Ассура.
, причём сила трения вычисляется через реакцию в паре, которую мы научились определять выше в силовом расчёте групп Ассура.


