
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристика сил, действующих в машинахСодержание книги
Поиск на нашем сайте
I. Движущие силы P д, или их моменты M д. Эти силы и моменты приложены к ведущим звеньям и приводят машины в действие. Их работа всегда имеет положительный знак, т. е. A д > 0. Это связано с тем, что движущие силы образуют острый угол с направлением движения звена, к которому они приложены. При решении задач кинетостатики двигателей эти силы задаются в виде индикаторных или силовых диаграмм. В технологических машинах они подлежат определению. Необходимо иметь в виду, что в таких машинах, как двигатели внутреннего сгорания, такт сжатия требует затрат энергии, и в этом такте работа движущих сил не производится, а выполняемая работа является работой сил сопротивления. Однако работа движущих сил в такте расширения (рабочего хода) существенно больше работы сопротивления в такте сжатия. Поэтому в течение каждого цикла имеется превышение работы движущих сил над работой сил сопротивления, что позволяет двигателю быть двигателем. II. Силы полезного сопротивления P п.с., или их моменты M п.с. Эти силы и моменты приложены к ведомым звеньям, связанным с исполнительными органами машин, и поэтому являются силами и моментами производственных, или технологических сопротивлений. Их работа имеет отрицательный знак, т. е. A п.с. < 0, так как моменты направлены против угловых скоростей звеньев, а силы образуют с направлением скоростей движения тупые углы. При решении задач кинетостатики технологических машин эти силы задаются в виде механических характеристик, или силовых диаграмм. В некоторых технологических машинах, таких как поршневые компрессоры,в такте расширения сила давления сжатого газа выполняет положительную работу, и по этой причине относится к движущей силе. Однако затем в такте сжатия выполняемая силами сопротивления работа существенно больше положительной работы в такте расширения, поэтому поршневой компрессор и относится к технологическим машинам. III. Силы вредного сопротивления. К этим силам относятся силы трения F тр (или моменты сил трения M тр), которые возникают во всех кинематических парах в связи с наличием в них относительного движения звеньев. Они направлены всегда против движения звена в кинематической паре, поэтому совершают отрицательную работу, т. е. A тр < 0. В некоторых случаях силы трения выполняют положительную роль, например в тормозах или транспортных машинах в точках соприкосновения колёс с дорогой (автомобиль) или с рельсом (локомотив).
К силам вредного сопротивления относятся также силы сопротивления среды, в которой функционирует техническое устройство. Это – силы сопротивления движению в воздушной среде и силы сопротивления движению в воде и других средах. Однако изучение этих сил выходит за рамки данного курса и здесь они не рассматриваются. IV. Силы тяжести (или силы веса) G. Эти силы действуют в зоне притяжения Земли согласно закону всемирного тяготения и определяются произведением V. Силы инерции VI. Силы реакций связей в кинематических парах (или просто реакции в кинематических парах)
Полезно помнить, что, несмотря на то, что эти реакции равны и противоположны, они не уравновешивают друг друга, так как каждая из них приложена к своему звену. Реакции уравновешиваются в случае, если кинематическая пара рассматривается в сборе. Работа реакций в кинематической паре равна нулю, т. е.
Задачи кинетостатики
Основными задачами раздела являются: 1) определение реакций в кинематических парах механизмов с целью их использования в дальнейшем для прочностных расчётов звеньев и элементов кинематических пар, расчёта сил трения, КПД и т. д.; 2) определение уравновешивающей силы P ур или уравновешивающего момента M ур на ведущем звене. Для решения этих задач необходимо знать: 1) кинематическую схему механизма и кинематические размеры его звеньев; 2) массы и моменты инерции звеньев. 3) внешние силы, действующие в машинах (применительно к технологическим машинам должны быть известны силы полезного, то есть технологического сопротивления, применительно к машинам-двигателям необходимо знать движущие силы).
Для лучшего понимания задач кинетостатики и необходимых для этого исходных данных обратимся к примеру на рис. 4.2. Механизм, представленный на этом рисунке, является четырёхшарнирным кривошипно-коромысловым, к звену 3 которого присоединён исполнительный орган, например тигель плоскопечатной машины. На это звено против направления его движения действует момент сопротивления По всем указанным на схеме силам и моментам после кинетостатического расчета (анализа) должна быть полная ясность как в отношении их величин, так и в отношении направлений. Решение задачи может быть представлено в виде следующих ступеней: 1. И с х о д н ы е д а н н ы е: схема механизма со всеми кинематическими размерами его звеньев, массовые характеристики звеньев (массы – m, кг; моменты инерции – J, 2. П р е д в а р и т е л ь н ы й р а с ч ё т: силы веса звеньев ( 3. О с н о в н о й р а с ч ё т: реакции в кинематических парах: Расчёт сил инерции
Расчёт сил инерции относится к предварительному расчёту, предшествующему основной задаче определения реакций в кинематических парах. Силы инерции возникают во всех случаях, когда звенья движутся непрямолинейно и/или неравномерно. Рассмотрим три вида движения звеньев. П о с т у п а т е л ь н о е д в и ж е н и е з в е н а. Этот вид движения чаще всего относится к ползунам, движущимся относительно прямолинейных направляющих (рис. 4.3). Пусть при этом
В р а щ а т е л ь н о е д в и ж е н и е з в е н а. В этом движении находятся кривошипы, кулисы, коромысла и другие звенья механизмов. Возьмём стержневое звено ОА (рис. 4.4), вращающееся вокруг неподвижной точки О. Масса звена равна
Угловое ускорение звена вызывает появление инерционного момента (или момента сил инерции), направленного по отношению к нему в противоположную сторону В этой формуле момент инерции принимается относительно центра вращения и определяется как Частные случаи 1. 2. 3. П л о с к о-п а р а л л е л ь н о е д в и ж е н и е з в е н а. Такое движение совершают чаще всего шатуны механизмов. На рис. 4.5 изображён шатун, совершающий такое движение. Масса шатуна равна
Замечание. Как видим, для расчёта сил инерции необходимо знать ускорения, с которыми движутся звенья механизма. Поэтому кинетостатическому расчёту должен предшествовать кинематический анализ механизма.
Общие положения силового расчёта П р и н ц и п Д а л а м б е р а. Силовой расчёт механизмов выполняется на основе принципа Даламбера, позволяющего рассматривать подвижные системы, к которым относятся механизмы как неподвижные, так и находящиеся в равновесии. Принцип Даламбера можно сформулировать так: если к системе сил, действующих на подвижную систему, добавить силы инерции, то такую систему можно рассматривать как находящуюся в равновесии, и к ней применимы законы статики. П р и н ц и п о с в о б о ж д а е м о с т и. Если рассматривать механизм в целом, то имеющаяся в каждой кинематической паре, согласно принципу равенства действия и противодействия, пара сил (реакций), действующих по одной линии действия и равных по величине, уравновешивается и на равновесие механизма в целом не влияет. Так что даже в простом механизме определить эти реакции невозможно – они не войдут в уравнения равновесия. Для определения реакций необходимо механизм расчленить на части, каждая из которых была бы статически определима и в которой неизвестные реакции входили бы в число внешних сил и в уравнения равновесия. Принцип освобождаемости заключается, таким образом, в выделении части механизма путём разрушения некоторых кинематических пар и заменой в них связей реакциями, подлежащими определению. С т а т и ч е с к а я о п р е д е л и м о с т ь г р у п п А с с у р а.
Это равенство совпадает с условием существования группы Ассура, следовательно, группа Ассура является статически определимой кинематической цепью, и силовой расчёт механизмов производится по группам Ассура.
П о с л е д о в а т е л ь н о с т ь с и л о в о г о р а с ч ё т а м е х а н и з м а. Силовой расчёт начинается с последней группы Ассура, в состав которой входит исполнительный орган машины, на который, как известно, действуют силы полезных (производственных или технологических) сопротивлений. При расчёте технологических машин эти силы входят в число исходных данных. В последнюю очередь рассчитывается входное (ведущее) звено. М е т о д ы с и л о в о г о р а с ч ё т а. Здесь мы только перечислим эти методы. Итак, задачи силового расчёта решаются с применением следующих методов: – метод планов сил; – метод разложения сил; – аналитический метод; – метод «жёсткого рычага» Н. Е. Жуковского; – экспериментальный метод. 4.5. Метод планов сил Рассмотрим метод планов сил для групп Ассура 2-го класса. Схемы этих групп хорошо известны из разделов структуры и кинематического исследования механизмов. Начинаем изучение проблемы с простейшей группы 2-го класса – группы 5-го вида. Г р у п п а А с с у р а 2-г о к л а с с а 5-г о в и д а. Согласно принципуосвобождаемости, выделяем эту группу из механизма, освобождая от связей в кинематических парах и заменяя их реакциями. Схема группы представлена на рис. 4.7, а в масштабе
Сама же группа, как видим, состоит из двух ползунов 2 и 3, образующих поступательную кинематическую пару друг с другом. Ползун 2 при этом образует вращательную кинематическую пару A с отброшенным звеном 1, а звено 3 движется поступательно вдоль горизонтальных направляющих. В большинстве случаев и сила веса звена 2, и его сила инерции невелики из-за малости массы этого звена. Поэтому без ущерба для точности расчётов этими силами можно пренебречь. На ползун 3 действуют сила сопротивления Со стороны отброшенных звеньев действуют реакции Для решения задачи определения реакций запишем уравнение равновесия всей группы Ассура в векторной форме
в котором, согласно принципу Даламбера, учтём силу инерции звена 3. В этом уравнении первые три вектора подчёркнуты двумя чертами, как известные по величине и направлению. Другие два подчёркнуты одной чертой, так как вектор Выбрав масштаб плана сил Что касается реакции Г р у п п а А с с у р а 2-г о к л а с с а 2-г о в и д а. Рассмотрим группу Ассура второго класса второго вида, состоящую из шатуна 2 и ползуна 3 Группа изображается в масштабе Записываем уравнение равновесия всей группы в целом в векторной форме
Если результат расчёта по приведённому выражению оказывается отрицательным, то в дальнейшем направление
В этом уравнении первые три вектора известны полностью, третий вектор определится построением плана сил. Можно обойтись и без построения отдельного плана, если на предыдущем плане сил сначала построить векторы сил, действующих на звено 3, а затем на звено 2. Тогда необходимые векторы сгруппируются, как часть плана сил группы Ассура, и остаётся только соединить конец вектора Измерив векторы на плане сил и умножив их на масштаб плана, получим физические величины искомых реакций. Г р у п п а А с с у р а 2-г о к л а с с а 1-г о в и д а. Эта группа представлена на рис. 4.9. Она состоит из двух стержневых звеньев 1 и 2 и трёх кинематических вращательных пар. С целью упрощения нагрузим звенья группы произвольной системой сил, не вдаваясь в их природу. Особенностью расчёта данной группы Ассура является то, что, в отличие от предыдущей группы, здесь приходится раскладывать на составляющие две реакции, в точках A и C.
Сразу же разложим неизвестные реакции в крайних шарнирах на тангенциальные и нормальные составляющие согласно равенствам – в шарнире A:
Для определения нормальных составляющих и полных реакций составляется уравнение равновесия сил, действующих на оба звена группы, в векторной форме
в котором сначала записаны векторы сил, действующих на звено 2, затем векторы сил, действующих на звено 3. Известные по величине и направлению векторы подчёркнуты двумя чертами, известные только по направлению – одной чертой. Они и подлежат определению с помощью плана сил. Его построение производится без затруднений на основе и с использованием предшествующего материала, поэтому здесь не рассматривается. Чтобы определить реакцию во внутренней кинематической паре B группы, необходимо так же, как и в предыдущей группе, построить план сил звена 2 отдельно от звена 3 по уравнению Если на плане сил группы Ассура векторы сил, действующих на звено 2, сосредоточены в одной зоне и не перемешиваются с векторами сил, действующими на звено 3, то нетрудно найти положение отрезка, соответствующего искомой реакции Г р у п п а А с с у р а 2-г о к л а с с а 3-г о в и д а. Схема группы этого вида с действующими на её звенья силами представлена в масштабе
Теперь уравнение для построения плана сил приобретает вид Г р у п п а А с с у р а 2-г о к л а с с а 4-г о в и д а. Данная группа состоит из двух ползунов, связанных между собой вращательной кинематической парой. Она представлена на рис. 4.11 в масштабе С и л о в о й р а с ч ё т к р и в о ш и п а. Как и в случае группы Ассура, необходимо прежде составить расчётную схему, приложив известные силы (рис. 4.12, а). В точке А прикладывается реакция
Вместо уравновешивающего момента можно приложить уравновешивающую силу Если приложить к кривошипу вместо уравновешивающего момента уравновешивающую силу, то она войдёт в векторное уравнение равновесия и повлияет на реакцию
Метод разложения сил
|
|||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 766; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.26.154 (0.011 с.) |

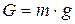 , где m – масса звена, кг; g – ускорение свободного падения, равное
, где m – масса звена, кг; g – ускорение свободного падения, равное  . Силы веса приложены в центре тяжести звена и направлены всегда к центру Земли, т. е. вертикально вниз. При движении звена вниз силы веса совершают положительную работу, при движении вверх – отрицательную работу. За цикл движения звена суммарная работа этих сил равна нулю.
. Силы веса приложены в центре тяжести звена и направлены всегда к центру Земли, т. е. вертикально вниз. При движении звена вниз силы веса совершают положительную работу, при движении вверх – отрицательную работу. За цикл движения звена суммарная работа этих сил равна нулю.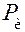 , или их моменты
, или их моменты 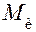 . Эти силы возникают во всех случаях, когда имеет место неравномерное и/или непрямолинейное движение звена. Они направлены против соответствующих ускорений (линейного или углового). Работа сил инерции может быть как положительной, так и отрицательной, в зависимости от направления этих сил по отношению к скорости движения звена, однако сумма этих работ за цикл движения равна нулю.
. Эти силы возникают во всех случаях, когда имеет место неравномерное и/или непрямолинейное движение звена. Они направлены против соответствующих ускорений (линейного или углового). Работа сил инерции может быть как положительной, так и отрицательной, в зависимости от направления этих сил по отношению к скорости движения звена, однако сумма этих работ за цикл движения равна нулю.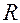 . Реакция в кинематической паре возникает в результате того, что под действием сил, приложенных к одному из звеньев пары, это звено стремится совершить движение в направлении действия сил, однако другое звено препятствует этому. Согласно одному из основных постулатов механики, любое действие вызывает равное и противоположно направленное противодействие, поэтому со стороны другого звена появляется реакция, противоположная направлению равнодействующей сил, приложенных к первому звену.
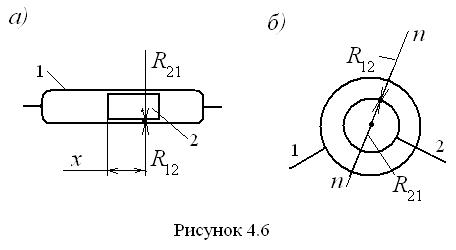
. Реакция в кинематической паре возникает в результате того, что под действием сил, приложенных к одному из звеньев пары, это звено стремится совершить движение в направлении действия сил, однако другое звено препятствует этому. Согласно одному из основных постулатов механики, любое действие вызывает равное и противоположно направленное противодействие, поэтому со стороны другого звена появляется реакция, противоположная направлению равнодействующей сил, приложенных к первому звену.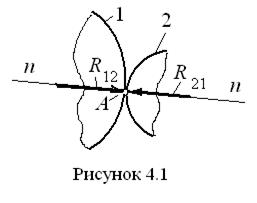 В первом приближении, т. е. при неучёте сил трения в кинематической паре, реакции направляются вдоль нормали в точке контакта элементов кинематической пары (рис. 4.1). На указанном рисунке изображены элементы звеньев 1 и 2, образующих кинематическую пару с контактом в точке A. Через эту точку проведена нормаль n - n к элементам кинематической пары, на которой располагаются реакции в точке A. Реакции обозначены, как отмечено выше, буквой
В первом приближении, т. е. при неучёте сил трения в кинематической паре, реакции направляются вдоль нормали в точке контакта элементов кинематической пары (рис. 4.1). На указанном рисунке изображены элементы звеньев 1 и 2, образующих кинематическую пару с контактом в точке A. Через эту точку проведена нормаль n - n к элементам кинематической пары, на которой располагаются реакции в точке A. Реакции обозначены, как отмечено выше, буквой 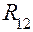 – это реакция первого звена на второе,
– это реакция первого звена на второе, 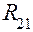 – это реакция второго звена на первое; естественно, что имеет место равенство
– это реакция второго звена на первое; естественно, что имеет место равенство 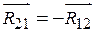 .
.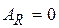 , так как в направлении их действия отсутствует движение.
, так как в направлении их действия отсутствует движение.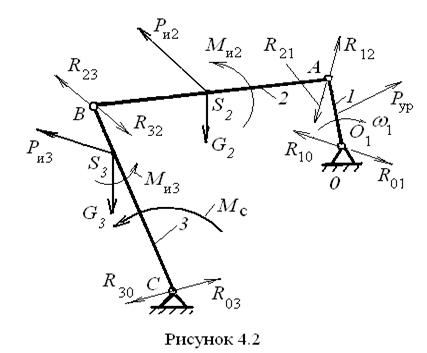
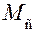 , являющийся полезной нагрузкой. Движение механизма происходит в результате действия на ведущий кривошип 1 движущей силы, являющейся одновременно уравновешивающей силой
, являющийся полезной нагрузкой. Движение механизма происходит в результате действия на ведущий кривошип 1 движущей силы, являющейся одновременно уравновешивающей силой 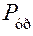 . Под её действием кривошип вращается по направлению движения часовой стрелки с угловой скоростью ω 1. На звенья механизма действуют также силы веса звеньев, силы инерции и, конечно, реакции в кинематических парах.
. Под её действием кривошип вращается по направлению движения часовой стрелки с угловой скоростью ω 1. На звенья механизма действуют также силы веса звеньев, силы инерции и, конечно, реакции в кинематических парах.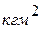 ): звена 1 – m 1,
): звена 1 – m 1, 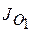 , звена 2 – m 2,
, звена 2 – m 2, 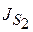 , звена 3 – m 3,
, звена 3 – m 3, 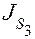 .
.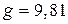
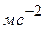 ) – G 1, G 2, G 3; силы инерции и моменты сил инерции звеньев –
) – G 1, G 2, G 3; силы инерции и моменты сил инерции звеньев – 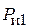 , Н;
, Н; 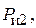 Н,
Н, 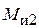 , Нм;
, Нм;  , Н,
, Н, 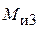 , Нм.
, Нм.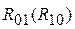 – в кинематической паре O 1,
– в кинематической паре O 1, 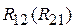 – в кинематической паре A,
– в кинематической паре A, 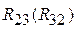 – в кинематической паре B,
– в кинематической паре B, 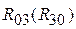 – в кинематической паре C. Уравновешивающая сила
– в кинематической паре C. Уравновешивающая сила 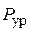 на кривошипе, приводящая в действие механизм.
на кривошипе, приводящая в действие механизм.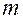 – масса ползуна,
– масса ползуна, 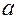 – его ускорение.
– его ускорение.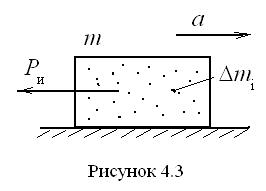 Сила инерции элементарной массы звена
Сила инерции элементарной массы звена 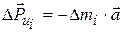 . Если просуммировать все элементарные силы инерции данного ползуна, то есть найти сумму
. Если просуммировать все элементарные силы инерции данного ползуна, то есть найти сумму 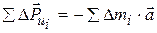 , то получится главный вектор сил инерции звена, равный
, то получится главный вектор сил инерции звена, равный 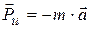 . То есть главный вектор сил инерции, или просто сила инерции звена в его поступательном движении равна массе звена, помноженной на его ускорение. Знак «−» в правой части формулы указывает на противоположность направления силы инерции по отношению к ускорению.
. То есть главный вектор сил инерции, или просто сила инерции звена в его поступательном движении равна массе звена, помноженной на его ускорение. Знак «−» в правой части формулы указывает на противоположность направления силы инерции по отношению к ускорению.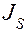 . Вращение происходит с угловой скоростью
. Вращение происходит с угловой скоростью 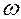 и угловым ускорением
и угловым ускорением 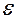 . Расстояние между центром масс и центром вращения равно
. Расстояние между центром масс и центром вращения равно 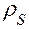 .
.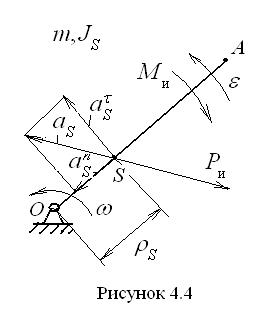 Вычислим ускорение, с которым движется центр масс S. Его нормальное ускорение равно
Вычислим ускорение, с которым движется центр масс S. Его нормальное ускорение равно 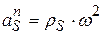 , тангенциальное ускорение равно
, тангенциальное ускорение равно 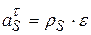 . Так как эти составляющие полного ускорения перпендикулярны друг другу, то полное ускорение
. Так как эти составляющие полного ускорения перпендикулярны друг другу, то полное ускорение 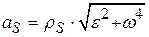 . Результатом этого ускорения является сила инерции, приложенная в центре масс и направленная противоположно ускорению
. Результатом этого ускорения является сила инерции, приложенная в центре масс и направленная противоположно ускорению 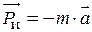 .
.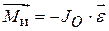 .
.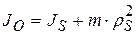 .
.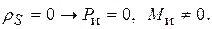
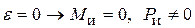 .
.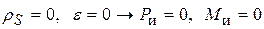 .
.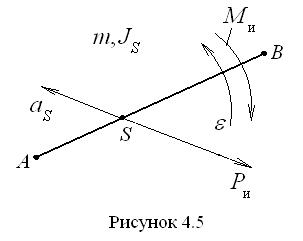 Звено движется, имея угловое ускорение
Звено движется, имея угловое ускорение 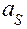 . Аналогично вращательному движению в этом случае также будут действовать оба инерционных фактора: сила инерции
. Аналогично вращательному движению в этом случае также будут действовать оба инерционных фактора: сила инерции 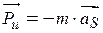 , противоположная ускорению центра масс, и момент сил инерции
, противоположная ускорению центра масс, и момент сил инерции 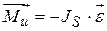 , противоположный угловому ускорению.
, противоположный угловому ускорению.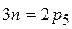 .
.
 , где отброшенные звенья изображены штриховыми линиями.
, где отброшенные звенья изображены штриховыми линиями.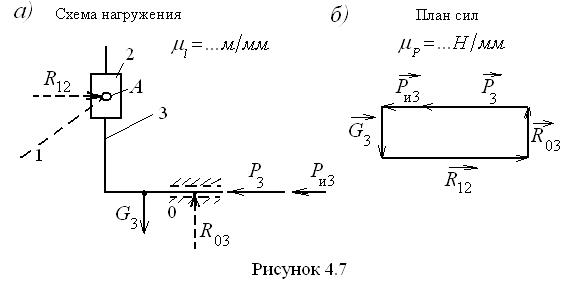
 , сила веса
, сила веса 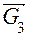 и сила инерции
и сила инерции 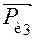 .
.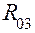 со стороны направляющих. Во внутренней поступательной паре группы действует реакция
со стороны направляющих. Во внутренней поступательной паре группы действует реакция 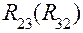 . Все три реакции подлежат определению. На схеме нагружения реакции показаны штриховыми линиями, так как точные направления их действия неизвестны.
. Все три реакции подлежат определению. На схеме нагружения реакции показаны штриховыми линиями, так как точные направления их действия неизвестны.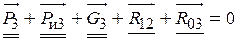 ,
,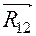 направлен по горизонтали в силу того, что, как было сказано выше, влиянием сил веса и сил инерции ползуна 2 мы пренебрегли из-за их малости, а вектор
направлен по горизонтали в силу того, что, как было сказано выше, влиянием сил веса и сил инерции ползуна 2 мы пренебрегли из-за их малости, а вектор 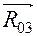 направлен перпендикулярно направляющим ползуна 3.
направлен перпендикулярно направляющим ползуна 3.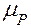 и поделив на него известные значения сил, строим векторный многоугольник в порядке их записи в уравнении (рис. 4.7, б). В этом многоугольнике все векторы по обходу контура направлены в одну сторону, т. е. нет ни одного вектора, направленного навстречу остальным. Это соответствует условию равновесия системы сил, действующих на группу Ассура.
и поделив на него известные значения сил, строим векторный многоугольник в порядке их записи в уравнении (рис. 4.7, б). В этом многоугольнике все векторы по обходу контура направлены в одну сторону, т. е. нет ни одного вектора, направленного навстречу остальным. Это соответствует условию равновесия системы сил, действующих на группу Ассура.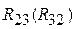 , то из-за невесомого ползуна 2 она будет равна реакции во вращательной паре A, т. е. имеют место равенства:
, то из-за невесомого ползуна 2 она будет равна реакции во вращательной паре A, т. е. имеют место равенства: 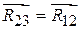 и
и 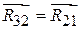 . В заключение вычисляются физические величины сил реакций с использованием масштаба плана
. В заключение вычисляются физические величины сил реакций с использованием масштаба плана 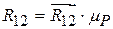 , Н и
, Н и 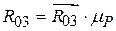 , Н.
, Н.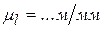 . На ползун 3 действует внешняя сила
. На ползун 3 действует внешняя сила 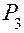 и сила инерции ползуна
и сила инерции ползуна 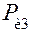 , на шатун действуют сила инерции
, на шатун действуют сила инерции 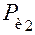 , приложенная в центре масс S 2, и момент сил инерции
, приложенная в центре масс S 2, и момент сил инерции 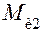 . Крайними кинематическими парами группы Ассура являются вращательная пара в точке А и поступательная пара ползуна 3 со стойкой. Отбрасывая кривошип 1 и стойку 0, освобождаем группу Ассура от связей и вместо них прикладываем неизвестные реакции
. Крайними кинематическими парами группы Ассура являются вращательная пара в точке А и поступательная пара ползуна 3 со стойкой. Отбрасывая кривошип 1 и стойку 0, освобождаем группу Ассура от связей и вместо них прикладываем неизвестные реакции 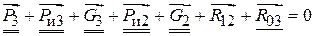 .
.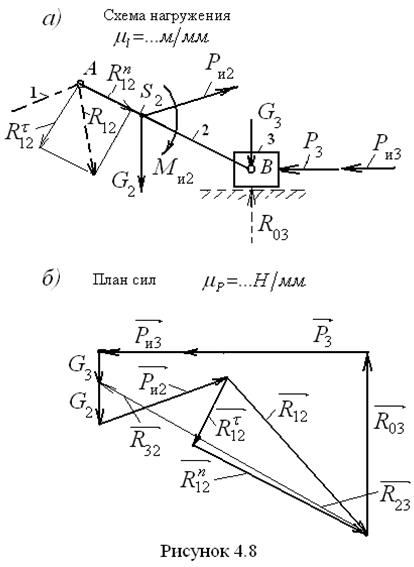 В правой части этого уравнения стоит нуль, указывающий на равновесие. В этом уравнении первые пять векторов, подчёркнутых двумя чертами, известны по величине и направлению. Шестой вектор неизвестен полностью, поэтому не подчёркнут совсем. Последний вектор, представляющий реакцию в поступательной паре, направлен перпендикулярно направляющей и подчёркнут одной чертой. Уравнение в таком виде не может быть решено, так как в нём три неизвестных параметра, а необходимо только два. Для сокращения количества неизвестных разложим вектор
В правой части этого уравнения стоит нуль, указывающий на равновесие. В этом уравнении первые пять векторов, подчёркнутых двумя чертами, известны по величине и направлению. Шестой вектор неизвестен полностью, поэтому не подчёркнут совсем. Последний вектор, представляющий реакцию в поступательной паре, направлен перпендикулярно направляющей и подчёркнут одной чертой. Уравнение в таком виде не может быть решено, так как в нём три неизвестных параметра, а необходимо только два. Для сокращения количества неизвестных разложим вектор 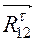 , направим перпендикулярно шатуну 2 и назовём тангенциальной составляющей. Вторую,
, направим перпендикулярно шатуну 2 и назовём тангенциальной составляющей. Вторую, 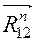 , направим вдоль шатуна и назовём нормальной составляющей. Данная операция соответствует равенству
, направим вдоль шатуна и назовём нормальной составляющей. Данная операция соответствует равенству 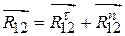 . Составляющая
. Составляющая 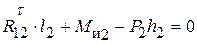 , из которого имеем
, из которого имеем 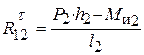 . Размеры плеч в этих выражениях измеряются в миллиметрах (
. Размеры плеч в этих выражениях измеряются в миллиметрах (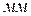 ) на схеме механизма и с помощью масштаба переводятся в натуральную величину. Причём, плечо
) на схеме механизма и с помощью масштаба переводятся в натуральную величину. Причём, плечо 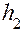 есть кратчайшее расстояние линии действия силы
есть кратчайшее расстояние линии действия силы 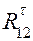 следует принять обратным по отношению к принятому на схеме. Составляющая
следует принять обратным по отношению к принятому на схеме. Составляющая 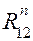 и реакция
и реакция 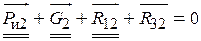 .
.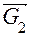 отрезком прямой, который и представит искомый вектор
отрезком прямой, который и представит искомый вектор 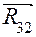 . Этот вектор направлен к началу
. Этот вектор направлен к началу 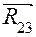 , который можно было бы получить построением плана сил звена 3 отдельно от звена 2.
, который можно было бы получить построением плана сил звена 3 отдельно от звена 2.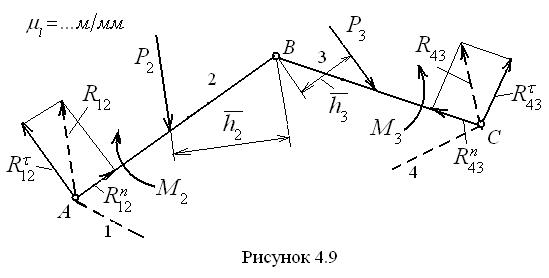
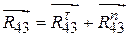 . При этом направляем тангенциальные составляющие перпендикулярно соответствующим звеньям, нормальные – вдоль звеньев. Для определения
. При этом направляем тангенциальные составляющие перпендикулярно соответствующим звеньям, нормальные – вдоль звеньев. Для определения 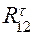 составляем уравнение равновесия звена 2 в форме моментов относительно точки B:
составляем уравнение равновесия звена 2 в форме моментов относительно точки B: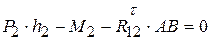 , из которого следует
, из которого следует 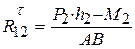 . Для определения
. Для определения 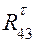 составляем уравнение равновесия в форме моментов сил звена 3 относительно точки B:
составляем уравнение равновесия в форме моментов сил звена 3 относительно точки B: 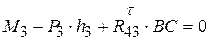 . Из этого уравнения следует, что
. Из этого уравнения следует, что 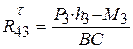 . Необходимо иметь в виду, что, если результаты расчётов тангенциальных составляющих окажутся с отрицательным знаком, то в дальнейших расчётах их направления должны быть приняты обратными указанным на схеме.
. Необходимо иметь в виду, что, если результаты расчётов тангенциальных составляющих окажутся с отрицательным знаком, то в дальнейших расчётах их направления должны быть приняты обратными указанным на схеме.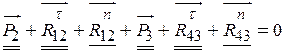 ,
,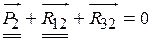 , или план сил звена 3 отдельно от звена 2 по уравнению
, или план сил звена 3 отдельно от звена 2 по уравнению 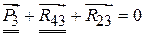 . Так как имеет место равенство
. Так как имеет место равенство 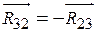 , то из этих двух вариантов достаточно выбрать один.
, то из этих двух вариантов достаточно выбрать один.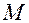 против часовой стрелки и сила
против часовой стрелки и сила 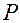 , как показано на рисунке. В большинстве практических случаев звено 2 (кулисный камень) выполнено таким образом, что его размеры и масса невелики и ими можно пренебречь. Тогда реакция
, как показано на рисунке. В большинстве практических случаев звено 2 (кулисный камень) выполнено таким образом, что его размеры и масса невелики и ими можно пренебречь. Тогда реакция 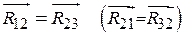 . В связи с этим заключаем, что
. В связи с этим заключаем, что 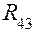 в паре B, то она неизвестна ни по величине, ни по направлению.
в паре B, то она неизвестна ни по величине, ни по направлению.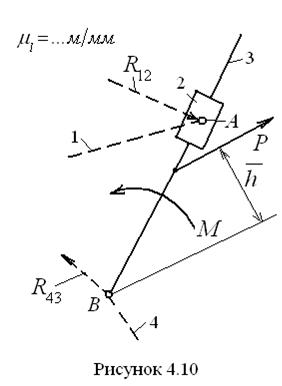 Для построения плана сил записываем уравнение равновесия всей группы в целом в векторной форме
Для построения плана сил записываем уравнение равновесия всей группы в целом в векторной форме 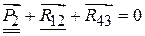 , подчеркнув в нём двумя чертами первый вектор, как известный по величине и направлению, и одной чертой второй вектор, как известный только по направлению линии действия. В этих условиях план сил не строится, так как в уравнении имеется три неизвестных вместо двух. Однако в связи с тем, что
, подчеркнув в нём двумя чертами первый вектор, как известный по величине и направлению, и одной чертой второй вектор, как известный только по направлению линии действия. В этих условиях план сил не строится, так как в уравнении имеется три неизвестных вместо двух. Однако в связи с тем, что  . Решая это уравнение относительно
. Решая это уравнение относительно  . Если результат расчёта получится отрицательным, то это значит, что на самом деле реакция
. Если результат расчёта получится отрицательным, то это значит, что на самом деле реакция 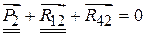 (в нём появилась вторая черта под вектором
(в нём появилась вторая черта под вектором 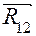 ) и может быть решено графическим путём. Это решение не представляет трудностей, поэтому здесь его опустим. В заключение необходимо измерить искомые векторы сил и умножить их на масштаб плана.
) и может быть решено графическим путём. Это решение не представляет трудностей, поэтому здесь его опустим. В заключение необходимо измерить искомые векторы сил и умножить их на масштаб плана.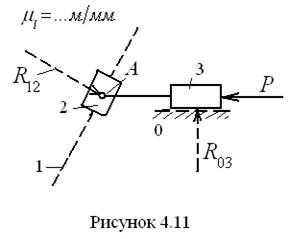 же, как и ранее, имеется в виду, что ползун 2 невесом, и на него не действуют никакие внешние силы. Векторное уравнение для построения плана сил с целью определения неизвестных реакций запишется так:
же, как и ранее, имеется в виду, что ползун 2 невесом, и на него не действуют никакие внешние силы. Векторное уравнение для построения плана сил с целью определения неизвестных реакций запишется так: 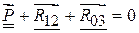 . В нём двумя чертами подчёркнута заданная, известная по величине и направлению сила, и одной чертой подчёркнуты силы, известные только по направлению. План сил (в данном случае треугольник) легко строится, и в нём также легко находятся искомые величины векторов в виде сторон треугольника. После их умножения на масштаб плана определяются физические величины реакций
. В нём двумя чертами подчёркнута заданная, известная по величине и направлению сила, и одной чертой подчёркнуты силы, известные только по направлению. План сил (в данном случае треугольник) легко строится, и в нём также легко находятся искомые величины векторов в виде сторон треугольника. После их умножения на масштаб плана определяются физические величины реакций 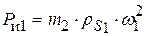 . Она направлена к точке А (это соответствует постоянству угловой скорости
. Она направлена к точке А (это соответствует постоянству угловой скорости 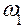 кривошипа). В точке О кривошипа действует реакция
кривошипа). В точке О кривошипа действует реакция 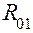 со стороны стойки, которую необходимо определить. Кроме того, к кривошипу необходимо приложить так называемый уравновешивающий момент
со стороны стойки, которую необходимо определить. Кроме того, к кривошипу необходимо приложить так называемый уравновешивающий момент 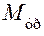 , действующий на него со стороны машины-двигателя, приводящей в движение данную машину.
, действующий на него со стороны машины-двигателя, приводящей в движение данную машину.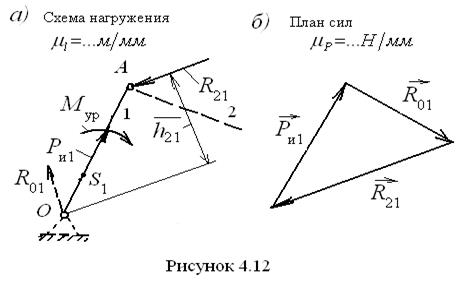
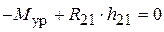 , из которого ясно, что
, из которого ясно, что 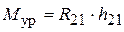 . Для нахождения реакции
. Для нахождения реакции 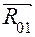 строится план сил согласно векторному уравнению
строится план сил согласно векторному уравнению 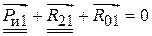 (рис. 4.12, б). В этом уравнении первые два вектора подчёркнуты дважды, т. к. они известны и по величине, и по направлению. Третий вектор неизвестен, поэтому не подчёркнут. Треугольник сил, в данном случае, нетрудно построить.
(рис. 4.12, б). В этом уравнении первые два вектора подчёркнуты дважды, т. к. они известны и по величине, и по направлению. Третий вектор неизвестен, поэтому не подчёркнут. Треугольник сил, в данном случае, нетрудно построить.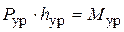 , в котором плечо
, в котором плечо 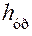 уравновешивающей силы и её направление должны быть выбраны произвольно.
уравновешивающей силы и её направление должны быть выбраны произвольно. Метод основан на двух известных из механики положениях, утверждающих, что, во-первых, если твёрдое тело (звено механизма) находится в равновесии под действием трёх сил, то линии действия этих сил пересекаются в одной точке. Во-вторых, любая сила может быть разложена по правилу параллелограмма по любым двум направлениям. Кроме того, здесь уч
Метод основан на двух известных из механики положениях, утверждающих, что, во-первых, если твёрдое тело (звено механизма) находится в равновесии под действием трёх сил, то линии действия этих сил пересекаются в одной точке. Во-вторых, любая сила может быть разложена по правилу параллелограмма по любым двум направлениям. Кроме того, здесь уч 


