
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения энергии в механике. Общефизический закон сохранения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим систему материальных точек и обозначим:
Тогда результирующая всех сил:
Умножим (1) скалярно на малое перемещение
Выясним физический смысл:
Перепишем (35) в виде:
или Принимая во внимание, что
Если система замкнута, то на нее внешние силы не действуют и
Если в системе не действуют неконсервативные силы, например силы трения, то
(37) – математическая формулировка закона сохранения механической энергии: - полная энергия замкнутой механической системы не меняется с течением времени. Однако в реальных системах механическая энергия, отдельно взятая, не сохраняется. В любой реальной системе при движении тел возникают силы трения, которые являются неконсервативными силами. В этом случае Поэтому рассмотренный нами закон сохранения и превращения механической энергии является частным случаем всеобщего физического закона сохранения и превращения энергии.
Абсолютно упругий и абсолютно неупругий центральные удары. Абсолютно упругий центральный удар подчиняется закону сохранения импульса и закону сохранения механической энергии: ЗСИ: ЗСЭ: Абсолютно неупругий центральный удар наличие общей скорости после соударения ЗСИ: ЗСЭ:
где
Твердое тело в механике. Уравнение вращательного движения твердого тела относительно точки.
Запишем для i-той материальной точки II закон Ньютона:
Умножим слева обе части (38) векторно на
Видно, что
В самом деле:
причем:
Перепишем уравнение (39) с учетом (40):
Векторное произведение радиус-вектора точки на ее импульс называется моментом импульса точки относительно т. О:
Векторное произведение радиус-вектора точки приложения силы на вектор этой силы называется моментом силы относительно т. О.
Перпендикуляр С учетом (41) и (43) перепишем (40) в виде:
Записывая аналогичные уравнения для всех n точек твердого тела и суммируя их почленно, получим:
Векторная сумма Векторная сумма моментов внешних сил, приложенных ко всем точкам системы, называется результирующим или главным моментом внешних сил относительно т. О:
Наконец, векторная сумма моментов всех внутренних сил относительно т. О равна нулю:
Это уравнение называется уравнением вращательного движения твердого тела относительно неподвижной точки.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 505; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.008 с.) |

 - результирующая всех внешних сил, действующих на систему;
- результирующая всех внешних сил, действующих на систему; - результирующая всех внутренних консервативных сил;
- результирующая всех внутренних консервативных сил;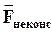 - результирующая всех внутренних неконсервативных сил, действующих на материальные точки.
- результирующая всех внутренних неконсервативных сил, действующих на материальные точки. (34)
(34) :
: (35)
(35) - работа результирующей силы, которая, как было установлено ранее, равна приращению
- работа результирующей силы, которая, как было установлено ранее, равна приращению  кинетической энергии системы:
кинетической энергии системы: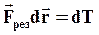
 - работа внешних сил;
- работа внешних сил; - работа консервативных сил, равная убыли потенциальной энергии системы:
- работа консервативных сил, равная убыли потенциальной энергии системы:
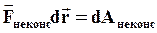 - работа неконсервативных сил.
- работа неконсервативных сил.
 (36)
(36) , где
, где  - полная энергия системы, получим:
- полная энергия системы, получим:
 , тогда:
, тогда:
 и
и , т.е.
, т.е.  (37)
(37)




 - выделившееся после соударения тепло;
- выделившееся после соударения тепло; - кинетическая энергия тел до соударения;
- кинетическая энергия тел до соударения; - кинетическая энергия тел после соударения.
- кинетическая энергия тел после соударения.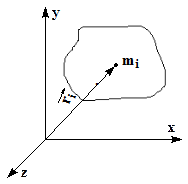
 ,
, 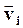 - масса и скорость i-той точки;
- масса и скорость i-той точки;
 - ее радиус-вектор;
- ее радиус-вектор;
 - внутренняя сила, действующая на i-тую точку со стороны k-той;
- внутренняя сила, действующая на i-тую точку со стороны k-той;
 - равнодействующая всех внешних сил, действующих на i -тую точку.
- равнодействующая всех внешних сил, действующих на i -тую точку.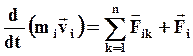 (38)
(38) (39)
(39) (40)
(40)

 (41)
(41) (42)
(42)
 находится по правилу векторного произведения. Для случая на рисунке
находится по правилу векторного произведения. Для случая на рисунке  , и направлен вверх. Модуль момента импульса равен:
, и направлен вверх. Модуль момента импульса равен:
 ,
,  (43)
(43)
 (11)
Направление
(11)
Направление  покажем на рисунке.
Модуль момента силы равен:
покажем на рисунке.
Модуль момента силы равен:  (44)
где
(44)
где  ,
, 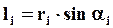
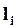 , опущенный из т.О на направление вектора силы, называется плечом этой силы.
, опущенный из т.О на направление вектора силы, называется плечом этой силы. (45)
(45) (46)
(46) называется моментом импульса тела относительно т. О.
называется моментом импульса тела относительно т. О.
 , т.к. момент каждой пары внутренних сил
, т.к. момент каждой пары внутренних сил  и
и 
 равен нулю. Тогда уравнение (40) примет вид:
равен нулю. Тогда уравнение (40) примет вид: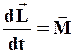 (47)
(47)


