Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Угловая скорость подвижного трехгранника, относительно другого трехгранникаСодержание книги
Поиск на нашем сайте
Существуют три независимых коэффициента разложения векторов
Определение вектора угловой скорости подвижного трехгранника на оси этого подвижного трехгранника.
Вектор угловой скорости трехгранника
Аналогично: БИЛЕТ 7.
Существует такой вектор
Определение вектора угловой скорости подвижного трехгранника на оси этого подвижного трехгранника.
Вектор угловой скорости трехгранника
Аналогично: Определение: угловой скоростью АТТ будем называть угловую скорость подвижного трехгранника, жестко связанного с АТТ. Корректно ли такое определение? Угловая скорость тела не зависит от выбора начала координат или полюса.
В подвижном трехграннике проекции не изменяются.
Пусть С- произвольная точка АТТ.
Таким образом, доказана теорема о независимости угловой скорости от выбора полюса. Где бы ни находилось начало трехгранника, угловая скорость остается одной и той же.
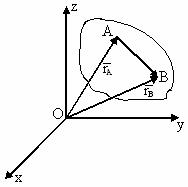
БИЛЕТ 8. Пусть
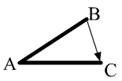
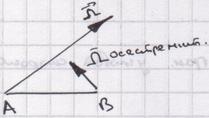
Точка В относительно точки А движется по окружности постоянного радиуса.
Теорема (о проекциях скоростей на прямую, их соединяющую). Проекции скоростей двух точек твёрдого тела на прямую, их соединяющую равны между собой. Доказательство.
БИЛЕТ 9. Проведем дифференцирование формулы Эйлера.
где
БИЛЕТ 10. Поступательным движением АТТ называется такое движение АТТ, при котором любая прямая, проведённая в АТТ, остаётся параллельной своему начальному положению.
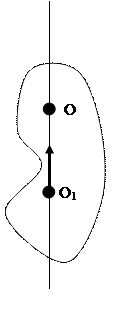
Вращающим движением а.т.т. относительно неподвижной оси называется такое движение, когда в теле существует такие 2 т-ки, такие что
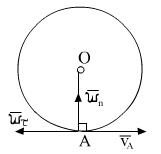
т. А движется по окружности, т.к. расстояние от точки О до А
Величина скорости точки = модулю расстояния угловой скорости и расстояния до оси вращения. Вектор скорости т. А
По формуле Ривальса:
Вторая составляющая ускорения называется осестремительным ускорением.
БИЛЕТ 12.
Плоско-параллельное движение АТТ. Называется такое движение, при котором скорости всех точек АТТ параллельны некоторой неподвижной в пространстве плоскости.
Пример1. Безотрывное движение (скольжение) АТТ по неподвижной плоскости и скорости всех точек будут параллельны плоскости.
Пример 2. Качение цилиндра. Скорости всех точек цилиндра будут перпендикулярны образующим цилиндра. Вращение вокруг неподвижной оси – частный случай плоско параллельного движения.
Аналогично:
Угловая скорость АТТ перпендикулярна неподвижной плоскости. Скорости всех точек, лежащих на одном перпендикуляре плоскости
Распределение скоростей в любом сечении плоскостью, || -ной плоскости
.
Эти уравнения определяют движение плоского сечения.
Формула Эйлера:
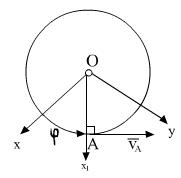
Для нахождения кинематического угла следует в начало графа т.А поместить ось x, затем от оси х к
Для плоскопараллельного движения:
БИЛЕТ 13.
|
||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 675; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

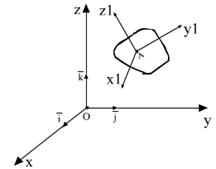
 - неподвижный трехгранник.
- неподвижный трехгранник.  .
.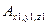 - жестко связ с АТТ.
- жестко связ с АТТ.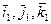 - единичные вектора
- единичные вектора 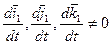
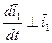 . Рассмотрим разложение вектора
. Рассмотрим разложение вектора 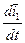 по векторам
по векторам 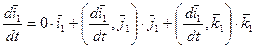
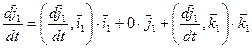
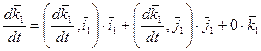
 ,
, 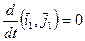


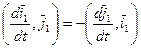
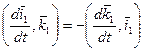
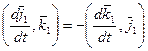
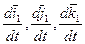 по векторам
по векторам 


 (1)
(1) 
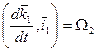
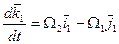
 (2)
(2)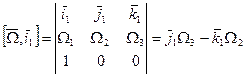
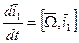 (3)
(3)
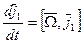 (3)
(3)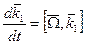 (3)
(3)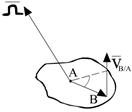
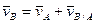 ,
,  где
где 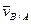 - скорость движения в точке В относительно точки А
- скорость движения в точке В относительно точки А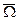 - угловая скорость АТТ.
- угловая скорость АТТ.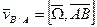
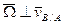

 .
.
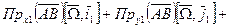

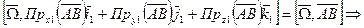
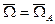 , А- полюс.
, А- полюс. 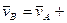
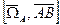 .
.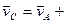
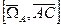 .
.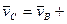
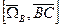 .
.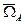 - угловая скорость для точки А.,
- угловая скорость для точки А., 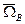 - угловая скорость для точки В.
- угловая скорость для точки В.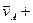
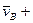

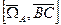 =
= 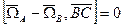

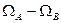
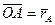
 ,
, 
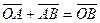
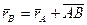
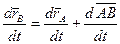
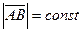 (из определения АТТ).
(из определения АТТ).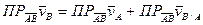
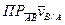 =0, так как
=0, так как 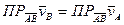 , что и требовалось доказать.
, что и требовалось доказать.
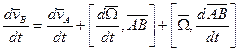
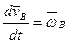 ,
,  ,
, 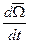 =
=  - угловое ускорение АТТ,
- угловое ускорение АТТ, 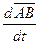 =
= 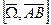 .
.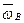
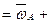
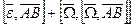 - формула Ривальса.
- формула Ривальса.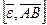 - тангенциальное ускорение,
- тангенциальное ускорение, 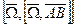 - осестремительное ускорение.
- осестремительное ускорение.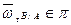
 ,
, 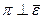 прох. через В.
прох. через В.
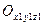 - подвижный трехгранник, связанный с АТТ.
- подвижный трехгранник, связанный с АТТ. 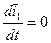 ,
,  ,
, 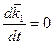
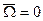 ,
, 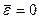
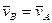
 БИЛЕТ 11.
БИЛЕТ 11.
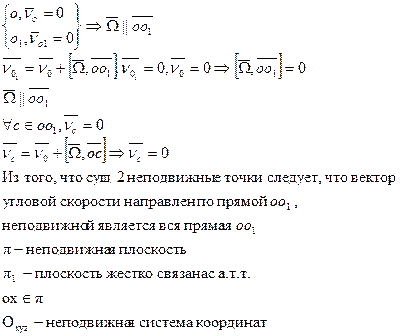

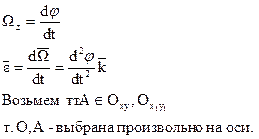

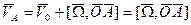
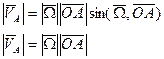
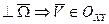
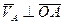
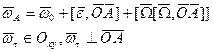
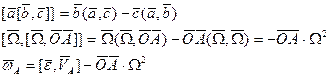


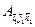 жестко связанос АТТ
жестко связанос АТТ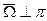



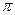 одинаковы.
одинаковы.
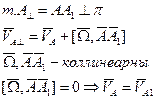
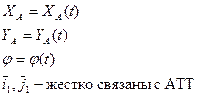
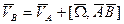
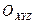 - неподв. трехгр-к.
- неподв. трехгр-к.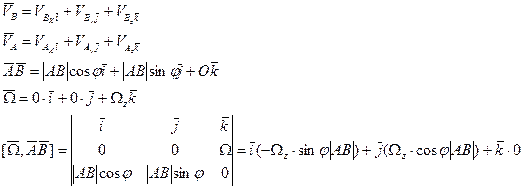
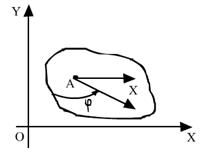
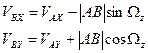

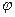 - кинематический угол
- кинематический угол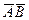 отсчитать угол против часовой стрелки, тогда:
отсчитать угол против часовой стрелки, тогда: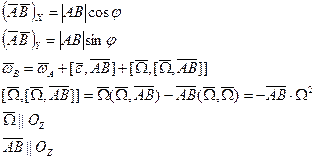

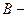 проекции на оси
проекции на оси 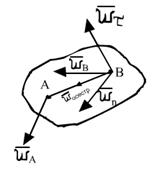
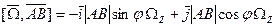


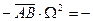
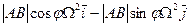
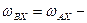
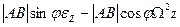
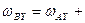

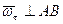 ,
,