
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мгновенный центр скоростей плоского сечения.Содержание книги Поиск на нашем сайте
МЦС плоского сечения называется такая точка, скорость в которой в данный момент времени = 0
Теорема: Если угловая скорость плоского сечения отлично от нуля, то МЦС существует и он единственен.
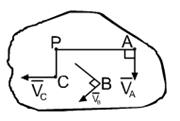
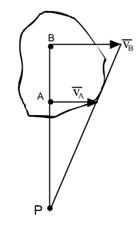
Доказательство: Пусть S-плоское сечение
Пусть т. а) б) Направление на
Выберем
Но
Согласно определению векторного произведения:
Таким образом существование МЦС доказано. Докажем теперь единственность. Пусть существует две точки P1, P2 Возьмем произвольную точку
Значит точки P1, P2 совпадают. ч.т.д.
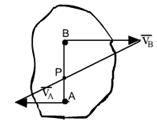
Понятие МЦС позволяет построить картину распределения векторов скоростей в плоском сечении. Таким образом:
Вектор скорости любой точки плоского сечения перпендикулярен радиусу, проведенному из МЦС.
а) б) Скорость точки плоского сечения пропорциональна расстоянию т этой точки до МЦС
т.к.
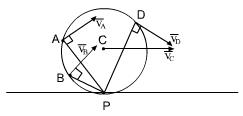
Способы нахождения МЦС. Мгновенное поступательное движение
2).
3).
4). Распределение скоростей в диске, катящемся по неподвижной плоскости без проскальзывания.
Циклоида.
БИЛЕТ 14. Пусть
Вектор
Таким образом:
Локальная производная:
Полная производная вектора
Теорема о сложении скоростей: Сложное движение материальной точки Сложным движением материальной точки называется движение, которое складывается из движения точки относительно подвижной с.к. и движения точки вместе с подвижной с.к. Движение точки относительно неподвижной с.к. называется абсолютным движением. Движение точки относительно подвижной с.к. называется относительным движением. Движение точки с подвижной с.к. называется переносным движением.
Пусть координаты точки в подвижной системе координат будут
где
Так как вектор
представляет собой относительную производную от
Переносной скоростью называется абсолютная скорость точки принадлежащей подвижной с.к., в которой в данный момент находиться точка.
Абсолютная скорость точки в сложном движении равна геометрической сумме скорости точки относительной и переносной.
БИЛЕТ 15. Будем называть сложным или «абсолютным» движением точки ее движение по отношению к системе координат, выбранной за основную. Движение точки по отношению к подвижной системе координат будем называть относительным. Под переносным, движением будем понимать движение подвижной системы координат относительно неподвижной.
Ускорение точки принадлежащей подвижной с.к. и находящаяся в данный момент там же где находиться точка M – переносное ускорение.
Относительным ускорением называется ускорение точки относительно подвижной с.к.
Абсолютным ускорением называется ускорение точки относительно неподвижной с.к.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.166.45 (0.009 с.) |

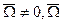 направлен к нам
направлен к нам
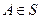
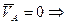 А-МЦС
А-МЦС
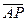 выберем в соответствии с направлением вращения т.е. повернем
выберем в соответствии с направлением вращения т.е. повернем 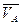 на 90 против часовой стрелки.
на 90 против часовой стрелки.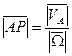

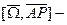 вектор
вектор 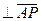 и
и 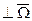 , принадлежащий сечению.
, принадлежащий сечению.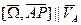
 (по построению точки Р)=
(по построению точки Р)= 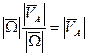
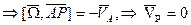
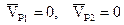 .
. 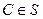 . Тогда по формуле Эйлера:
. Тогда по формуле Эйлера:

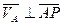 ,
, 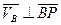 и так далее.
и так далее.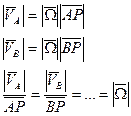



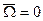

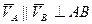
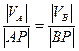
 Скорость направлена по касательной к направлению движения.
Скорость направлена по касательной к направлению движения.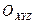 - неподвижный трехгранник с
- неподвижный трехгранник с  .
. 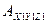 -подвижный с
-подвижный с 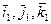
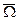 -вектор угловой скорости, угловая скорость в подвижной СК относительно неподвижной СК.
-вектор угловой скорости, угловая скорость в подвижной СК относительно неподвижной СК.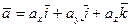 и
и 
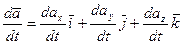 ,
, 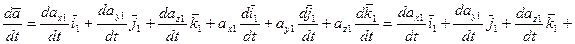

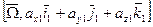 .
.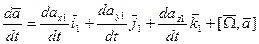 ., где
., где 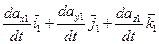 - производная от вектора
- производная от вектора 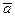 относительно неподвижного трехгранника.
относительно неподвижного трехгранника.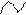
 - производная вектора
- производная вектора 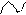 Полная производная:
Полная производная: 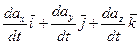

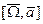 - Формула Бура.
- Формула Бура.  Если радиус-вектор
Если радиус-вектор 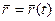 определяет положение точки М по отношению к системе координат
определяет положение точки М по отношению к системе координат 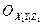 , радиус-вектор
, радиус-вектор 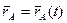 определяет положение начала системы координат
определяет положение начала системы координат 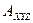 в системе
в системе  определяет положение точки М в системе координат
определяет положение точки М в системе координат 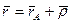
 тогда
тогда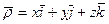
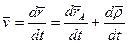
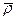 определен в подвижной системе координат, то для нахождения абсолютной производной от него воспользуемся формулой
определен в подвижной системе координат, то для нахождения абсолютной производной от него воспользуемся формулой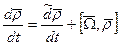
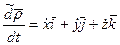
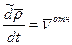 - скорость точки с относительной с.к.-относительная скорость
- скорость точки с относительной с.к.-относительная скорость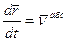 -скорость точки относительно неподвижной с.к.- абсолютная скорость точки
-скорость точки относительно неподвижной с.к.- абсолютная скорость точки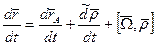
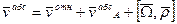
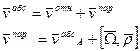
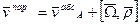 -переносной скоростью называется абсолютная скорость точки принадлежащей подвижной с.к., в которой в данный момент находиться точка.
-переносной скоростью называется абсолютная скорость точки принадлежащей подвижной с.к., в которой в данный момент находиться точка.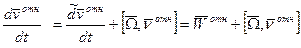
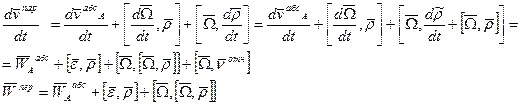
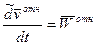 -локальная производная относительно скорости.
-локальная производная относительно скорости.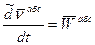 -абсолютное ускорение
-абсолютное ускорение



