
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о сложении ускоренийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Абсолютное ускорение равно геометрической сумме переносного, относительного и добавочного (ускорения Кориолиса) ускорений.
Движение по трубе вдоль оси y – движение относительное Суперпозиция или наложение даст нам движение абсолютное.
Иллюстрация к теореме о сложении скоростей.
Иллюстрация к теореме о сложении ускорений.
Три закона Ньютона. I Если на м.т. не действуют никакие силы, то т-ка сохраняет состояние покоя или равномерного прямолинейного движения. Замечание: Движение относительно! Существуют такие системы отсчета, в которых 1 з-н Ньютона выполняется, такие системы отсчета называются инерциальными. II Если на т-ку действует сила, то она создает ускорение пропорциональное этой силе III Если на материальная т-ка 1 действует материальную на т-ку 2 с силами F12, то 2-ая точка действует на 1 точку с силами F21 = - F21 Некоторые вопросы о силе Определение: Сила – это количественная мера взаимодействия материальных тел, это вектор, который определяется величиной, направлением и точкой приложения. Аксиомы: 1) Силы приложенные в одной точке можно складывать по правилу параллелограмма 2) Силы можно переносить вдоль линии действия Следствие: Система сил, линия действия которых пересекаются, можно заменить одной силой приложенной к точке пересечения линий действия сил, и такая система пересекающихся сил приводиться к равновесию и называется приводящей к равнодействующей. Прямая и обратная задача динамики точки.
Рассмативается свободная материальная точка массой По второму закону Ньютона:
1). Прямая задача.
Дано:
Нужно найти Решается путем интегрирования дифференциальных уравнений.
2). Обратная задача. Дано: Определить силы, под действием которых тело движется. Если продифференцировать
БИЛЕТ 17. Момент силы относительно точки. Моментом силы относительно точки называется векторное произведение радиуса-вектора точки приложения силы на вектор силы.
По определению векторного произведения
Плечо силы- длина перпендикуляра, опущенного из той точки, относительно которой вычисляется момент силы, на линию действия этой силы.
Вектор момента относительно точки Момент силы зависит от точки, относительно которой вычисляется момент. Момент силы может быть равен нулю, если точка, относительно которой вычисляется момент, лежит на линии действия силы.
+
Проекции вектора момента силы
Момент силы относительно оси.
БИЛЕТ 18. Главный вектор и главный момент системы сил.
Главным вектором системы сил называется геометрическая сумма всех сил системы.
При изменении точки приведения системы сил главный вектор системы сил не изменяется, а главный момент меняется.
Изменение точки приведения:
Главный момент системы относительно точки
Условие равновесия системы сил: система сил или система АТТ, на которую действует система сил находится в равновесии тогда и только тогда, когда равны нулю главный вектор системы сил и главный момент системы сил.
Это условие сохраняется при изменении точки приведения.
БИЛЕТ 19.
Парой сил называется система двух сил, равных по величине и противоположных по направлению. Линии действия этих сил параллельны. Расстояние межу этими линиями действия сил называется плечом пары.
Плоскость, в которой лежат прямые называется плоскостью пары.
Теорема: момент пары сил не зависит от точки, относительно которой этот момент вычисляется. Момент пары сил равен моменту одной из сил, составляющих пару, относительно точки приложения другой.
Момент пары сил:
Не зависит от выбора точки
Как расположены плоскости для эквивалентной пары сил?- Они параллельны.
Чему равен главный вектор пары сил? = 0.
БИЛЕТ 20.
По третьему закону Ньютона:
Тогда для
Главный вектор внутренних сил БИЛЕТ 21. Количеством движения материальной точки называется сумма произведений масс на их скорость.
По третьему закону Ньютона:
Тогда для
Главный вектор внутренних сил
Производная по времени от вектора количества движения равна главному вектору внешних сил.
Система материальных точек называется замкнутой, если на нее не действуют внешние силы; и если на систему не действуют внешние силы, то вектор количества движения (импульса) есть величина постоянная.
БИЛЕТ 22. Центр масс системы материальных точек - это точка, полжение которой в пространстве опредляется вектором
Связь вектора количества движения со скоростью центра масс:
Тогда из теоремы изменения количества движения следует теорема о движении центра масс: Центр масс системы движется как материальная точка, в которой сосредоточена вся масса системы и на которую действует сила, равная главному вектору внешних сил.
Если
БИЛЕТ 23. Кинетическим моментом системы материальных точек относительно точки
Инерциональная с.о.
Пример:
|
||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.196.177 (0.009 с.) |

 Движение вокруг оси z – переносное движение
Движение вокруг оси z – переносное движение



 , на которую действуют силы, сумма которых обозначим:
, на которую действуют силы, сумма которых обозначим:  .
.
 .
.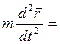


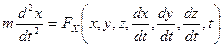


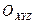 - инерциальная система координат.
- инерциальная система координат. ,
, 


 то есть
то есть 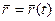
 .
.



 ,
,  ,
,  - правая тройка векторов.
- правая тройка векторов. параллелограмма.
параллелограмма.
 - плечо силы.
- плечо силы. параллелограмма =
параллелограмма = 
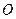 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов  Поместим начало системы координат в точку
Поместим начало системы координат в точку 



 .
.





 Момент силы относительно оси - произведение проекции силы на плоскость, перпендикулярную оси, на плечо проекции. Скалярная величина.
Момент силы относительно оси - произведение проекции силы на плоскость, перпендикулярную оси, на плечо проекции. Скалярная величина.




 - сумма векторов элементов всех сил, взятых относительно точки O.
- сумма векторов элементов всех сил, взятых относительно точки O. . При совершении этой операции допускается перенос всех векторов в точку O.
. При совершении этой операции допускается перенос всех векторов в точку O.



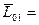
 равен главному моменту системы относительно точки
равен главному моменту системы относительно точки 




 перпендикулярен плоскости пары.
перпендикулярен плоскости пары.
 Момент пары сил полностью характеризует пару.
Момент пары сил полностью характеризует пару. Все точки системы находятся под действием силы.
Все точки системы находятся под действием силы. - силы, действующие на точки системы со стороны внешних по отношению к этой системе тел.
- силы, действующие на точки системы со стороны внешних по отношению к этой системе тел. - силы, действующие между точками системы.
- силы, действующие между точками системы. - сила, действующая на
- сила, действующая на  -ю точку со стороны
-ю точку со стороны  - й точки системы.
- й точки системы. . Они равны по модулю и действуют по прямой, их соединяющей, в противоположные стороны.
. Они равны по модулю и действуют по прямой, их соединяющей, в противоположные стороны.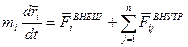
 - слева.
- слева. =
=  .
. , потому что все силы встречаются парами равными по величине и противоположными по направлению.
, потому что все силы встречаются парами равными по величине и противоположными по направлению. - вектор количества движения.
- вектор количества движения.
 - теорема об изменении количества движения системы материальных точек в инерциальной системе отсчета.
- теорема об изменении количества движения системы материальных точек в инерциальной системе отсчета. ,
, 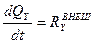 ,
,  .
. .
. .
. Координаты центра масс:
Координаты центра масс:





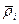 - радиус-вектор относительно центра масс.
- радиус-вектор относительно центра масс. , но
, но 




 , где
, где 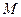 - масса всей системы.
- масса всей системы.  - скорость центра масс.
- скорость центра масс.
 = 0, то центр масс системы находится в покое или в состоянии равномерного прямолинейного движения.
= 0, то центр масс системы находится в покое или в состоянии равномерного прямолинейного движения. называется сумма векторных произведений радиус-векторов относительно точки
называется сумма векторных произведений радиус-векторов относительно точки 








