
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стандартные матрицы ориентации.Содержание книги Поиск на нашем сайте
ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ 1. Векторный и координатный (декартовы координаты), способы задания движения материальной точки. Скорость и ускорение точки для векторного и координатного (декартовы координаты) способов задания движения точки. 2. Естественный способ задания движения материальной точки. Скорость и ускорение точки для естественного способа задания движения. 3. Матрица взаимной ориентации двух трехгранников (матрица направляющих косинусов). Свойства строк и столбцов матрицы ориентации. 4. Стандартные матрицы ориентации. 5. Параметры ориентации твердого тела: углы Эйлера. Матрица направляющих косинусов как функция углов Эйлера. 6. Понятие угловой скорости одного трехгранника относительно другого. 7. Угловая скорость абсолютно твердого тела. Теорема о независимости угловой скорости от выбора полюса. 8. Связь между скоростями двух точек твердого тела. Теорема о проекциях скоростей двух точек твердого тела на прямую, их соединяющую. 9. Связь между ускорениями двух точек твердого тела (вращательное и осестремительное ускорения). Угловое ускорение твердого тела. 10. Поступательное движение твердого тела. Скорости и ускорения точек при поступательном движении твердого тела. 11. Вращение абсолютно твердого тела вокруг неподвижной оси. Уравнение вращательного движения. Скорости и ускорения точек твердого тела. 12. Плоско-параллельное движение абсолютно твердого тела. Уравнения плоскопараллельного движения. Скорости и ускорения точек твердого тела, направление угловой скорости и углового ускорения. 13. Понятие мгновенного центра скоростей (МЦС) при плоском движении твердого тела. Теорема о существовании и единственности МЦС. Способы нахождения МЦС. 14. Сложное движение точки: понятия абсолютной, относительной и переносной скоростей. Связь между производными вектора относительно разных трехгранников (формула Бура). Теорема о сложении скоростей. 15. Сложное движение точки: понятия абсолютного, относительного, переносного и кориолисова (добавочного) ускорений. Теорема о сложении ускорений (теорема Кориолиса). 16. Три закона Ньютона. Прямая и обратная задачи динамики. 17. Момент силы относительно точки. Проекции момента силы относительно точки на оси координат. Момент силы относительно оси.
18. Главный момент системы сил относительно точки. Главный вектор системы сил. Изменение главного момента при переносе точки приведения. 19. Пара сил. Независимость главного момента пары сил от центра приведения. Момент пары сил. 20. Внешние и внутренние силы системы материальных точек. Свойства системы внутренних сил. 21. Количество движения (импульс) системы материальных точек. Теорема об изменении импульса. 22. Центр масс системы материальных точек. Связь импульса системы материальных точек со скоростью центра масс. Теорема о движении центра масс. 23. Момент количества движения (кинетический момент) системы материальных точек относительно произвольного центра приведения. Теорема об изменении кинетического момента системы материальных точек относительно произвольного центра приведения. Случай неподвижного центра приведения и случай, когда центр приведения совпадает с центром масс. 24. Работа и мощность системы сил. Мощность момента пары сил. Кинетическая энергия системы материальных точек. Момент инерции системы материальных точек относительно оси. Теорема об изменении кинетической энергии. 25. Кинетическая энергия для простейших движений абсолютно твердого тела. Момент инерции системы материальных точек относительно оси. Теорема Кенига для произвольного движения системы материальных точек. 26. Консервативные системы. Силовая функция, потенциальная энергия, потенциальные силы. Теорема о приращении кинетической энергии для консервативных систем. Полная механическая энергия. Закон сохранения полной механической энергии системы материальных точек для потенциальных сил. 27. Понятие связей, наложенных на механическую систему. Примеры связей. Уравнения связей. Классификация связей. Возможные перемещения и возможные скорости точек механической системы, допускаемые связями. Примеры. 28. Силы реакций связей. Аксиома освобождаемости от связей. Идеальные связи. Примеры. 29. Число степеней свободы механической системы, обобщенные координаты и обобщенные скорости. Примеры. 30. Обобщенные силы. Обобщенные силы реакции идеальных связей. 31. Даламберовы силы инерции. Принцип Даламбера-Лагранжа.
32. Принцип Даламбера-Лагранжа для систем с идеальными удерживающими связями. Принцип возможных перемещений. Условие равновесия системы с идеальными голономными стационарными связями. 33. Тождества Лагранжа. Дифференциальные уравнения движения механической системы с идеальными связями (уравнения Лагранжа второго рода). 34. Уравнения Лагранжа второго рода для потенциальных сил. Функция Лагранжа. Уравнения равновесия консервативных механических систем с идеальными голономными связями. 35. Уравнения плоскопараллельного движения абсолютно твердого тела. БИЛЕТ 1. Кинематика - это часть механики, которая занимается изучением движения материальных тел, не интересуясь причинами возникновения этого движения (с геометрической точки зрения).
Материальная точка - тело, размерами которого можно принебречь. Это модель.
Скорость точки при векторном и координатном способе задания движения. Векторный способ.
Координатный способ.
Сравниваем (1) и (2)
При координатном способе задания движения материальной точки вектор скорости определяется своими проекциями на оси координат, являющиеся неподвижными.
Направление вектора скорости можно задать с помощью углов, которые образуют вектор скорости с координатными осями.
Ускорение точки при векторном и координатном способе задания движения. Ускорением точки
Направляющие косинусы для
БИЛЕТ 2. Естественный способ задания движения точки. Движение точки заданно естественно, если: 1) Задана траектория 2) Начало отсчета 3) Задано направление отсчета 4) Известна длина дуги как функция времени.
Каждое положение точки на траектории характеризуется своим радиус-вектором. Зависимость точки
Так как длина дуги стремится к длине секущей при сближении точек (для достаточно гладких кривых), то длина этого вектора:
В каждой точке может быть введен
Вектор
Скалярное произведение двух не нулевых векторов равно нулю, если угол между ними
Вектор постоянной длины и переменного направления. Если его начало закрепить, то при движении он будет описывать сферу. Производная вектора есть скорость конца вектора, то есть величина, вектор которой направлен по касательной к сфере, а значит
Если кривая достаточно гладкая, т.е. вектор касательной резко не изменяет своего положения, то на малом перемещении Кривизна траектории характеризует изменение направления вектора
БИЛЕТ 3.
Плоскость, проходящая через вектора Плоскость, проходящая через вектора
9 координат, удовл. 3 уравнениям
В векторных пределах свободно можно выбрать (2) и (3) ограничив
Координаты начала подвижной системы координат.
Матрицей ориентации (матрицей направляющих косинусов) трехгранника называется
Независимыми являются только три. В силу свойств матрицей направляющих косинусов.
Пусть даны вектора
Векторным произведением двух векторов называется вектор, обладающий следующими свойствами: 1). Этот вектор перпендикулярен плоскости векторов 2). Вектора 3). Модуль
БИЛЕТ 4. БИЛЕТ 5. Углы Эйлера.
На На На
БИЛЕТ 6. БИЛЕТ 7.
Существует такой вектор
БИЛЕТ 8. Пусть
Точка В относительно точки А движется по окружности постоянного радиуса.
Доказательство.
БИЛЕТ 9. Проведем дифференцирование формулы Эйлера.
где
БИЛЕТ 10. Поступательным движением АТТ называется такое движение АТТ, при котором любая прямая, проведённая в АТТ, остаётся параллельной своему начальному положению.
Вращающим движением а.т.т. относительно неподвижной оси называется такое движение, когда в теле существует такие 2 т-ки, такие что
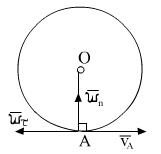
т. А движется по окружности, т.к. расстояние от точки О до А
Величина скорости точки = модулю расстояния угловой скорости и расстояния до оси вращения. Вектор скорости т. А
По формуле Ривальса:
Вторая составляющая ускорения называется осестремительным ускорением.
БИЛЕТ 12.
БИЛЕТ 13. Способы нахождения МЦС. 3).
4). Распределение скоростей в диске, катящемся по неподвижной плоскости без проскальзывания.
Циклоида.
БИЛЕТ 14. Пусть
Вектор
Таким образом:
Локальная производная:
Полная производная вектора
Теорема о сложении скоростей: БИЛЕТ 15. Будем называть сложным или «абсолютным» движением точки ее движение по отношению к системе координат, выбранной за основную. Движение точки по отношению к подвижной системе координат будем называть относительным. Под переносным, движением будем понимать движение подвижной системы координат относительно неподвижной.
Ускорение точки принадлежащей подвижной с.к. и находящаяся в данный момент там же где находиться точка M – переносное ускорение.
Относительным ускорением называется ускорение точки относительно подвижной с.к.
Абсолютным ускорением называется ускорение точки относительно неподвижной с.к.
Три закона Ньютона. I Если на м.т. не действуют никакие силы, то т-ка сохраняет состояние покоя или равномерного прямолинейного движения. Замечание: Движение относительно! Существуют такие системы отсчета, в которых 1 з-н Ньютона выполняется, такие системы отсчета называются инерциальными. II Если на т-ку действует сила, то она создает ускорение пропорциональное этой силе III Если на материальная т-ка 1 действует материальную на т-ку 2 с силами F12, то 2-ая точка действует на 1 точку с силами F21 = - F21 Некоторые вопросы о силе Определение: Сила – это количественная мера взаимодействия материальных тел, это вектор, который определяется величиной, направлением и точкой приложения. Аксиомы: 1) Силы приложенные в одной точке можно складывать по правилу параллелограмма 2) Силы можно переносить вдоль линии действия Следствие: Система сил, линия действия которых пересекаются, можно заменить одной силой приложенной к точке пересечения линий действия сил, и такая система пересекающихся сил приводиться к равновесию и называется приводящей к равнодействующей. Прямая и обратная задача динамики точки.
Рассмативается свободная материальная точка массой По второму закону Ньютона:
1). Прямая задача.
Дано:
Нужно найти Решается путем интегрирования дифференциальных уравнений.
2). Обратная задача. Дано: Определить силы, под действием которых тело движется. Если продифференцировать
БИЛЕТ 17. БИЛЕТ 18. БИЛЕТ 19.
Парой сил называется система двух сил, равных по величине и противоположных по направлению. Линии действия этих сил параллельны. Расстояние межу этими линиями действия сил называется плечом пары.
Плоскость, в которой лежат прямые называется плоскостью пары.
Теорема: момент пары сил не зависит от точки, относительно которой этот момент вычисляется. Момент пары сил равен моменту одной из сил, составляющих пару, относительно точки приложения другой.
Момент пары сил:
Не зависит от выбора точки
Как расположены плоскости для эквивалентной пары сил?- Они параллельны.
Чему равен главный вектор пары сил? = 0.
БИЛЕТ 20.
По третьему закону Ньютона:
Тогда для
Главный вектор внутренних сил БИЛЕТ 21. Количеством движения материальной точки называется сумма произведений масс на их скорость.
По третьему закону Ньютона:
|
||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 715; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.48.125 (0.015 с.) |

 Движение - изменение положения.
Движение - изменение положения.
 - радиус-вектор точки M.
- радиус-вектор точки M. - векторный закон движения точки.
- векторный закон движения точки.
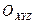 - принимаем за неподвижную.
- принимаем за неподвижную.  - едничные вектора.
- едничные вектора.

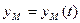 - движение задано координатным способом.
- движение задано координатным способом.


 ,
, 
 - средняя скорость за
- средняя скорость за 
 ,
,  - мгновенная скорость.
- мгновенная скорость.

 (1)
(1) (2)
(2) ,
,  ,
, 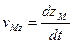 .
. . Эти проекции скорости равны производным от соответствующих координат. Знание проекций скорости позволяет найти ее величину и ее направление.
. Эти проекции скорости равны производным от соответствующих координат. Знание проекций скорости позволяет найти ее величину и ее направление. .
. ,
,  ,
, 
 Положение
Положение  стремится к касательной точки. Скорость в каждый момент времени направлена по касательной к траектории.
стремится к касательной точки. Скорость в каждый момент времени направлена по касательной к траектории.
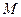 называется
называется  по времени.
по времени. ,
,  .
.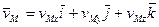 , так как
, так как 




 :
: ,
,  ,
,  .
.
 - естественный закон движения точки.
- естественный закон движения точки.  .
.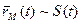 ,
,  .
. на траектории.
на траектории.
 ,
,  - вектор.
- вектор. . Вектор
. Вектор 
 - единичный вектор касательной.
- единичный вектор касательной. .
.  направлен в сторону увеличения
направлен в сторону увеличения  - проекция вектора скорости на направление касательной.
- проекция вектора скорости на направление касательной. Если
Если  , то
, то  . Если же
. Если же  , то
, то  .
. 


 .
.  -вектор
-вектор  .
.





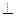 -ый измен. вектору.
-ый измен. вектору.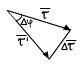


 ,
,  - кривизна траектории.
- кривизна траектории. угол изменяется на малую величину.
угол изменяется на малую величину. .
. 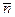 - единичный вектор.
- единичный вектор.  .
.

 , где
, где  . Если движение по окружности, то
. Если движение по окружности, то  радиусу окружности.
радиусу окружности. ,
,  .
. Естественный трехгранник (трехгранник Дарбу). Естественный способ задания движения точки.
Естественный трехгранник (трехгранник Дарбу). Естественный способ задания движения точки. ,
, 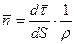 .
.  - единичный вектор бинормаль.
- единичный вектор бинормаль. образуют правый трехгранник. – сопровождающий трехгранник или трехгранник Дарбу.
образуют правый трехгранник. – сопровождающий трехгранник или трехгранник Дарбу.  ,
,  .
. - нормальная плоскость.
- нормальная плоскость. - соприкасающаяся плоскость.
- соприкасающаяся плоскость. Абсолютно твердым телом называется система материальных точек, растояние между которыми остается неизменным все время движения.
Абсолютно твердым телом называется система материальных точек, растояние между которыми остается неизменным все время движения.


 (1)
(1)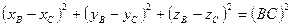 (2)
(2) (3)
(3) - независимые.
- независимые. , затем из (1) найти
, затем из (1) найти  .
.
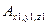 - жестко связ с АТТ.
- жестко связ с АТТ.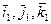 - единичные вектора
- единичные вектора  - неподвижные оси,
- неподвижные оси, 





 - матрица 3х3
- матрица 3х3


 .
.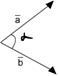 Определение: Скалярное произведение векторов
Определение: Скалярное произведение векторов  .
. , если
, если 
 =
=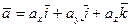 ,
, 
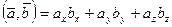
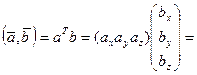 число.
число. составляют правую тройку векторов.
составляют правую тройку векторов. равен модулю
равен модулю  . Другими словами,
. Другими словами,  равен площади параллелограмма, построенного на векторах
равен площади параллелограмма, построенного на векторах 
 .
.
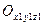 - подвижный трехгранник (связанный с АТТ).
- подвижный трехгранник (связанный с АТТ). - линия узлов.
- линия узлов.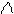
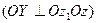 .
.

 - угол прецессии.
- угол прецессии.
 - угол нутации.
- угол нутации. - угол собтвенного вращения
- угол собтвенного вращения Все три угла определены, если
Все три угла определены, если  .
.
 - углы меняются со временем.
- углы меняются со временем. вокруг OY
вокруг OY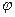 вокруг Oz
вокруг Oz 



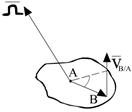
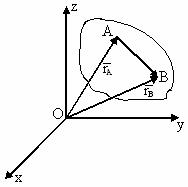
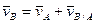 ,
,  где
где 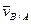 - скорость движения в точке В относительно точки А
- скорость движения в точке В относительно точки А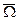 - угловая скорость АТТ.
- угловая скорость АТТ.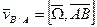
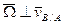
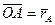
 ,
, 
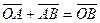
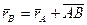
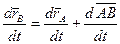
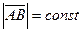 (из определения АТТ).
(из определения АТТ).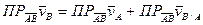
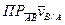 =0, так как
=0, так как 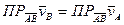 , что и требовалось доказать.
, что и требовалось доказать.
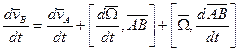
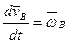 ,
,  ,
, 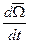 =
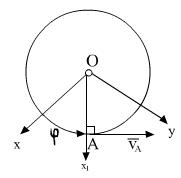
=  - угловое ускорение АТТ,
- угловое ускорение АТТ, 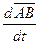 =
= 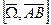 .
.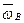
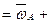
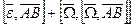 - формула Ривальса.
- формула Ривальса.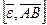 - тангенциальное ускорение,
- тангенциальное ускорение, 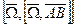 - осестремительное ускорение.
- осестремительное ускорение.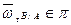
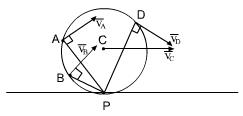
 ,
, 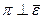 прох. через В.
прох. через В.
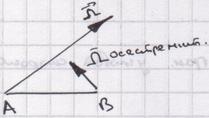
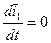 ,
,  ,
, 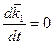
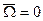 ,
, 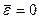
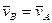
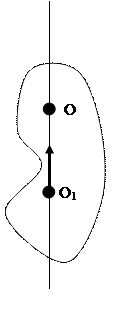 БИЛЕТ 11.
БИЛЕТ 11.
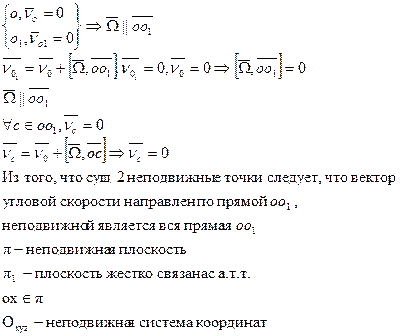

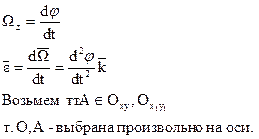

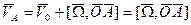
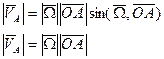
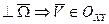
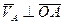
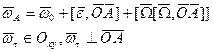
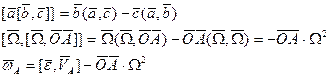

 Скорость направлена по касательной к направлению движения.
Скорость направлена по касательной к направлению движения.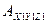 -подвижный с
-подвижный с 
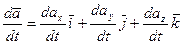 ,
, 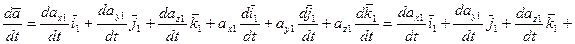

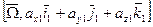 .
.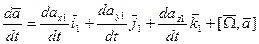 ., где
., где 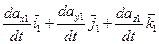 - производная от вектора
- производная от вектора 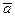 относительно неподвижного трехгранника.
относительно неподвижного трехгранника.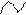
 - производная вектора
- производная вектора 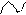 Полная производная:
Полная производная: 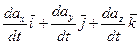

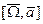 - Формула Бура.
- Формула Бура. 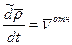 - скорость точки с относительной с.к.-относительная скорость
- скорость точки с относительной с.к.-относительная скорость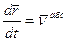 -скорость точки относительно неподвижной с.к.- абсолютная скорость точки
-скорость точки относительно неподвижной с.к.- абсолютная скорость точки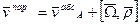 -переносной скоростью называется абсолютная скорость точки принадлежащей подвижной с.к., в которой в данный момент находиться точка.
-переносной скоростью называется абсолютная скорость точки принадлежащей подвижной с.к., в которой в данный момент находиться точка.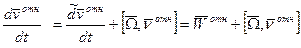
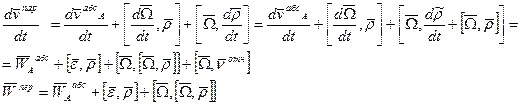
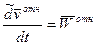 -локальная производная относительно скорости.
-локальная производная относительно скорости.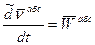 -абсолютное ускорение
-абсолютное ускорение
 , на которую действуют силы, сумма которых обозначим:
, на которую действуют силы, сумма которых обозначим:  .
.
 .
.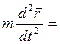


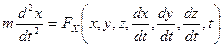


 ,
, 


 то есть
то есть 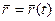
 .
.




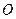

 перпендикулярен плоскости пары.
перпендикулярен плоскости пары.
 Момент пары сил полностью характеризует пару.
Момент пары сил полностью характеризует пару. Все точки системы находятся под действием силы.
Все точки системы находятся под действием силы. - силы, действующие на точки системы со стороны внешних по отношению к этой системе тел.
- силы, действующие на точки системы со стороны внешних по отношению к этой системе тел. - силы, действующие между точками системы.
- силы, действующие между точками системы. - сила, действующая на
- сила, действующая на  -ю точку со стороны
-ю точку со стороны  - й точки системы.
- й точки системы. . Они равны по модулю и действуют по прямой, их соединяющей, в противоположные стороны.
. Они равны по модулю и действуют по прямой, их соединяющей, в противоположные стороны.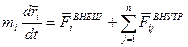
 - слева.
- слева. =
=  .
. , потому что все силы встречаются парами равными по величине и противоположными по направлению.
, потому что все силы встречаются парами равными по величине и противоположными по направлению. - вектор количества движения.
- вектор количества движения.


