
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рассмотрим следующие типы связей.Содержание книги Поиск на нашем сайте
1). Гибкая нерастяжимая нить (невесомый стержень).
2). Контакт двух гладких поверхностей.
3). Цилиндрический шарнир. Вообще говоря, направление сил реакции зависит от внешних нагрузок.
Связи называются идеальными, если работа сил реакции на возможном перемещении = 0. Примеры идеальных связей: Нерастяжимая нить.
Скольжение по гладкой поверхности.
Качение без проскальзывания.
БИЛЕТ 29.
Рассмотрим систему Это число и назовем числом степеней свободы системы.
Число степеней свободы = числу независимых возможных скоростей. Если на систему наложены { 1). Полностью определяют положение системы 2). Не зависят друг от друга.
Обобщенные координаты-
Обобщенные скорости:
Если введены обобщенные координаты
Скорость Если связи, наложенные на систему стационарные, то последнее слагаемое равно нулю.
При фиксированном
БИЛЕТ 30. Обобщенные силы.
Пусть в системе введены обобщенные координаты: Возможное перемещение: Тогда элементарная работа активных сил
Обобщенные силы- коэффициенты в разложении элементарной работы активных сил по вариации обобщенных координат. Размерность обобщенной силы зависит от размерности соотвествующей обобщенной координаты. Если обобщенная координаты угловая, то соответствующая обобщенная сила имеет размерность Обобщенная сила- скалярная величина.
Рассмотрим элементарную работу сил реакции связи.
Если связи, наложенные на систему являются идеальными, то
Рассмотрим систему материальных точек со связями:
………
БИЛЕТ 31. Принцип Даламбера:
БИЛЕТ 32. Принцип Даламбера: Сумма элементарных работ сил инерции, активных сил и сил реакции связи = 0. Если связи, наложенные на систему, идеальные, то Принцип Даламбера для систем с идеальными связями: сумма элементарных работ и элементарных сил на возможных перемещениях = 0. Пусть система материальных точек с идеальными связями находится в равновесии.
Принцип Даламбера: Необходимым и достаточным условием равновесие системы с идеальными связями является равенство нулю суммы элементарных работ активных сил на возможных перемещениях.
Принцип возможных перемещений- условие равновесия!!!!!!!!!!
Рассмотрим систему с идеальными связями. Обобщенные координаты
Следствие:
БИЛЕТ 33. Доказательство уравнения Лагранжа 2-го рода.
Тождество Лагранжа.
Для достаточно гладких функций:
БИЛЕТ 34. Уравнение равновесия консервативных систем (с идеальными голономными связями).
Идеальные голономные связи.
Из принципа возможных перемещений Для консервативных систем:
Решая эти уравнения, можно получить положение равновесия консервативной системы.
ДАНО:
Найти: положение равновесия.
Решение: Запишем потенциальную энергию.
Равенство нулю возможно в двух случаях: 1) 2).
|
||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.150.64 (0.011 с.) |

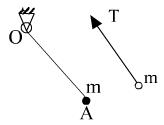


 4). Качение по шероховатой поверхности.
4). Качение по шероховатой поверхности.



 , так как возможное перемещение в точках контакта с поверхностью = 0.
, так как возможное перемещение в точках контакта с поверхностью = 0.
 4). Неподвижный цилиндрический шарнир.
4). Неподвижный цилиндрический шарнир.
 5). Подвижный шарнир.
5). Подвижный шарнир.
 материальных точек, на которую наложены
материальных точек, на которую наложены  голономных связей. Из
голономных связей. Из  вариаций декартовых координат точек системы независимыми будут только
вариаций декартовых координат точек системы независимыми будут только  .
. параметров
параметров ,
,  }, которые:
}, которые: Пример:
Пример:

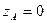 ,
, 
 - 4 уравнения голономных стацион. связей
- 4 уравнения голономных стацион. связей

 ,
, 

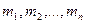 - всего
- всего 




 точки:
точки: 
 :
: 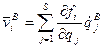 .
. не зависят друг от друга.
не зависят друг от друга. ,
, 

 ,
,  - силы реакции.
- силы реакции. (
( :
:  .
.
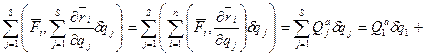
 , где
, где  - обобщенная активная сила.
- обобщенная активная сила.
 , то есть размерность момента.
, то есть размерность момента.
 , где
, где  - обобщ.сила реакции.
- обобщ.сила реакции. = 0
= 0 
 = 0
= 0 
 = 0,
= 0,  , …,
, …,  .
.  - независимы. Можно не говорить об обобщенных силах реакции в идеальных связях.
- независимы. Можно не говорить об обобщенных силах реакции в идеальных связях.


 - угловая скорость
- угловая скорость 
 .
. .
. ,
,  ,
,  .
. - прицип возможных перемещений.
- прицип возможных перемещений.


 . Так как
. Так как  .
.  - вариация
- вариация  - й обобщенной координаты.
- й обобщенной координаты. . Система с идеальными связями находится в равновесии тогда и только тогда, когда все обобщенные силы равны нулю.
. Система с идеальными связями находится в равновесии тогда и только тогда, когда все обобщенные силы равны нулю. -?
-?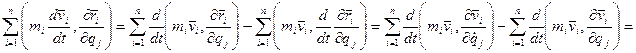
 .
.


 линейная функция от
линейная функция от 





 ,
,  - число степеней свободы.
- число степеней свободы.

 - уравнение равновесия консервативной системы.
- уравнение равновесия консервативной системы.

 - невесомый стержень.
- невесомый стержень.
 - жесткость пружины.
- жесткость пружины. - длина пружины в ненапряженном состоянии.
- длина пружины в ненапряженном состоянии. ,
,  текущая длина пружины.
текущая длина пружины.



 . (нижнее положение маятника). Устойчивое равновесие.
. (нижнее положение маятника). Устойчивое равновесие. . (верхнее положение маятника). Неустойчивое равновесие.
. (верхнее положение маятника). Неустойчивое равновесие.


