Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема об изменении кинетического момента.Содержание книги Поиск на нашем сайте
Производная по времени в инерциальной системе отсчета от вектора кинетического момента системы относительно точки 1). Если точка 2). Точка
Главный момент системы внутренних сил равен нулю, потому что силы встречаются парами, равными по величине, противоположными по направлению и направленными по одной прямой.
Таким образом,
БИЛЕТ 24.
Элементарная работа силы
Теорема: (об изменении кинетической энергии системы) Производная по времени от кинетической энергии системы равна сумме мощностей внутренних и внешних сил, действующих на точки системы. Приращение кинетической энергии системы материальных точек равно сумме элементарных работ внутренних и внешних сил, действующих на точки системы.
Доказательство: Система материальных точек.
Мощность момента пары сил, приложенных к АТТ.
=
БИЛЕТ 25. Поступательное движение АТТ.
При поступательном движении Вращение АТТ вокруг неподвижной оси.
+
«Кинетическая энергия АТТ в произвольном движении равна сумме кинетической энергии центра масс, как если бы в нем была сосредоточена вся масса АТТ и кинетической энергии движения относительно центра масс».
Плоское движение:
Движение относительно центра масс будет представлять собой движение вокруг оси
БИЛЕТ 26.
Системы сил называются консервативными, если работа этих сил не зависит от формы траектории, а определяется только начальной и конечной точкой. Работа консервативных сил по замкнутому контуру = 0.
Силы называются потенциальными, если существует такая скалярная функция, которая зависит или от радиуса вектора или от координат, что вектор силы
Если система сил потенциальна, то она является консервативной.
Найдем работу по перемещению из точки
Из теоремы об изменении кинетической энергии для консервативных систем: Если все внешние и внутренние силы консервативны, то Полная механическая энергия
Теорема (об изменении полной механической энергии для консервативных систем): Если система материальных точек консервативна, то ее полная механическая энергия есть величина постоянная: БИЛЕТ 27. Связями называется ограничение на движение материальной точки.
Плоский математический маятник.
Если бы они были свободны.
Аналитическая запись:
В зависимости от типа уравнений различаются и типы связей: 1). Стационарные связи (в уравнения которых не входит время). 2). Нестационарные связи (в уравнения которых входит время). 3). Односторонние связи 4). Двусторонние связи (выражаются уравнениями) 5). Геометрические связи (голономные).
6). Дифференцируемые (не голономные связи).
Возможные перемещения - перемещения, которые допускаются связями в данный момент времени.
Двусторонние и голономные связи:
………..
Вариации этих уравнений: При фиксированном
………..
Возможная скорость- скорость,которая допускается связями в данный момент времени.
Рассмотрим пример, когда точка находится на сфере постоянного радиуса. Ее возможное перемещение как и возможная скорость должна быть направлена по касательной к сфере или радиус-вектору.
Действительная скорость - одна из возможных.
Теперь рассмотрим случай, когда точка находится на сфере переменного радиуса.
Действительная скорость= одна из возможных скоростей + одна из скоростей.
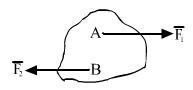
БИЛЕТ 28. Рассмотрим систему материальных точек
Аксиома освобождаемости от связей: Связи, наложенные на систему можно отбросить, заменив
Система свободных материальных точек но с силами реакции связи. Направление зависит от типа связей.
|
||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.244.1 (0.01 с.) |

 равна главному моменту внешних сил в двух случаях:
равна главному моменту внешних сил в двух случаях: =0)
=0)
 (
( )
) ,
,  - центр масс.
- центр масс. ,
,  - неподвижная точка.
- неподвижная точка. Мощностью силы
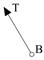
Мощностью силы  , приложенной к точке
, приложенной к точке 
 на элементарном перемещении точки
на элементарном перемещении точки  :
: 
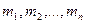
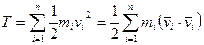

 (внутр.и внешн)
(внутр.и внешн)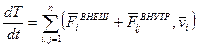
 (так как
(так как  )
)
 Пусть есть АТТ.
Пусть есть АТТ. 
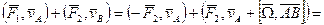
 =
= мощность пары можно записать так:
мощность пары можно записать так: = произведение угловой скорости на момент этой пары.
= произведение угловой скорости на момент этой пары.
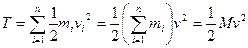





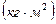

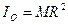


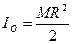

 -радиус инерции.
-радиус инерции.


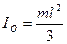

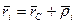
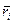 - радиус-вектор.
- радиус-вектор.  - относительно ц. масс.
- относительно ц. масс.
 +
+



 - Теорема Кёнига.
- Теорема Кёнига. плоскости движения.
плоскости движения.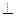 плоскости движения и проходящей через центр масс.
плоскости движения и проходящей через центр масс.


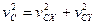

 (90
(90  ,
,  )
)



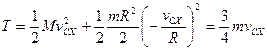
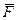 , действующей в точке
, действующей в точке  равен
равен  этой функции, или
этой функции, или  .
.  .
. .
.
 ,
,  ,
,  .
. 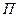 - потенциальная энергия, силовая функция.
- потенциальная энергия, силовая функция.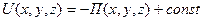 .
. ,
,  ,
,  .
. .
.
 .
. - потенциальная энергия. Работа не зависит от пути.
- потенциальная энергия. Работа не зависит от пути. - приращение потенциальной энергии.
- приращение потенциальной энергии.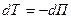
 .
. .
.

 ,
,  плоскости движения.
плоскости движения.
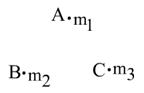 Система материальных точек.
Система материальных точек.


 АТТ.
АТТ.

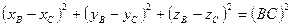 .
. ,
, 
 - уравнение связи для материальной точки, находящейся на поверхности сферы переменного радиуса.
- уравнение связи для материальной точки, находящейся на поверхности сферы переменного радиуса.


 . Не содержат в качестве аргументов скорости точек.
. Не содержат в качестве аргументов скорости точек.


 уравнений связи:
уравнений связи: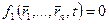







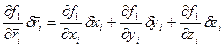

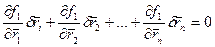
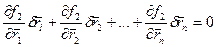 - уравнения для возможных перемещений.
- уравнения для возможных перемещений.
 векторных неизвестных.
векторных неизвестных.  .
. ,
,  ,
,  - возможные вариации в декартовых координатах.
- возможные вариации в декартовых координатах. вариаций подчиняются
вариаций подчиняются  . Говорят, что система имеет
. Говорят, что система имеет 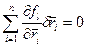
 - уравнение для возможных перемещений
- уравнение для возможных перемещений  - воображаемый промежуток времени.
- воображаемый промежуток времени. . Уравнение для возможных скоростей:
. Уравнение для возможных скоростей: 



 - силы, действующие на точки системы со строны внешних по отношению к системе сил, и внуренних. Они называются активными силами.
- силы, действующие на точки системы со строны внешних по отношению к системе сил, и внуренних. Они называются активными силами. - силы реакции связей.
- силы реакции связей. их действие силами реакции связи.
их действие силами реакции связи.