
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неудовлетворительность механики Ньютона при больших скоростяхСодержание книги
Поиск на нашем сайте Рассмотрим с точки зрения преобразований Галилея движение света.
В системе К' его скорость v'x= c. Тогда, используя полученный закон сложения скоростей из 8.2. для скорости света в системе К мы найдем:
Опубликованные в 1881 г. результаты опытов, выполненных американским физиком А. Майкельсоном, находятся в противоречии с только что полученной нами формулой: галилеевский закон сложения скоростей не годится для света. Скорость света оказалась одинаковой в разных системах отсчета! В 1895 г. французский математик, физик и философ А. Пуанкаре впервые выступил с новаторским предложением о невозможности никакими физическими опытами (не только механическими, как в принципе относительности Галилея) зарегистрировать абсолютное движение. В 1902 г. он же публикует в книге "Наука и гипотеза" утверждение об отсутствии абсолютного времени, т.е. t ≠ t'. Законченная теория, позволяющая описывать движение частиц со скоростями v → с, была опубликована в 1905 г. в работах А. Пуанкаре и А. Эйнштейна. Постулаты С.Т.О. Механика больших скоростей, специальная теория относительности (С.Т.О.), базируется на двух исходных утверждениях, постулатах: I. Принцип относительности, согласно которому Никакими физическими опытами нельзя установить, покоится ли данная система отсчета, либо движется равномерно и прямолинейно. Другая формулировка: Все законы природы одинаково формулируются для всех инерциальных систем отсчета. II. Принцип постоянства скорости света: cкорость света в вакууме во всех инерциальных системах отсчета одинакова и не зависит ни от движения источника, ни от движения приемника света. 8.5. Преобразования Лоренца - это уравнения, связывающие координаты и время некоторого события (8.1) в двух инерциальных системах отсчета. В отличие от преобразований Галилея преобразования Лоренца не должны противоречить постулатам С.Т.О.: необнаружимости абсолютного движения и постоянству скорости света. При скорости движения системы отсчета V<< c преобразования Лоренца должны переходить в преобразования Галилея. 8.5.1. Вывод преобразований Лоренца Для вывода преобразований Лоренца рассмотрим в двух системах отсчета мысленный опыт. Одна система К - неподвижна, другая К' движется вдоль оси х со скоростью V. Пусть в момент времени t = t' = 0, когда начала систем координат совпадали, в этом начале произошла вспышка света и стала распространяться сферическая световая волна. В соответствии с постулатом I фронт этой волны будет сферой в обеих системах отсчета, сфера эта будет, в соответствии с постулатом II, увеличивать свой радиус со скоростью света и в той, и в другой системе отсчета.
Опираясь на эти требования, найдем вид правильных преобразований координат и времени. В качестве пробного возьмем преобразование Галилея, а затем его подправим. x2 + y2 + z2 = c2t2: В системе К' уравнение фронта этой волны, в соответствии с постулатами I и II (x')2+(y')2+(z')2=c2 (t')2, пробуем преобразования Галилея, переходим в К: (x')2 = (x - Vt)2, (y')2 = y2, (z')2 = z2, (t')2 = t2, отсюда следует: x2 - 2Vxt + V 2 t 2 + y2 + z2 = c2t2, сравните с (x')2+(y')2+(z')2 = c2(t')2. Появились ЛИШНИЕ ЧЛЕНЫ, надо так изменить преобразования, чтобы они исчезли. x' = x- Vt, y'=y, z'=z, t'=t-αx приравниваем подчеркнутые члены, получаем:
При таком α остается:
Перегруппируем члены:
Подправим преобразование так, чтобы исчезли выражения в скобках, для этого возьмем
Такие преобразования сохраняют вид уравнения фронта световой волны, сфера преобразуется в сферу, в соответствии с постулатами С.Т.О. Обозначим, для удобства записи,
тогда преобразования Лоренца запишутся так:
Релятивистская механика должна быть построена таким образом, чтобы уравнения движения не менялись при переходе из одной инерциальной системы отсчета в другую, т.е. были инвариантны относительно преобразований Лоренца.
8.6. Следствия из преобразований Лоренца
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.195.105 (0.007 с.) |










 ;
;
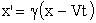 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.



