
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнетизм и магнитные явленияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Имени Н. И. Вавилова»
Магнетизм и магнитные явления Методические указания по изучению дисциплины и задания для контрольной работы студентам – заочникам электротехнических специальностей Саратов 2011 Составители: ст. преп. кафедры «Инженерная физика» Рыжова Е.В., доцент, кандидат физ.-мат. наук Пилипенко Е.А.
Магнетизм и магнитные явления: Методические указания по изучению дисциплины и задания для контрольной работы студентам – заочникам электротехнических специальностей. Общие методические указания Цель настоящих методических указаний – помочь студентам – заочникам электротехнических специальностей в изучении дисциплин «Магнетизм и магнитные явления» и «Электромагнитная индукция в инженерных устройствах». Руководство содержит краткое изложение теоретического материала дисциплины, описания инженерных устройств, в основе которых лежат магнитные явления, указания к решению задач с примерами решения, таблицу вариантов контрольных заданий (вариант выбирается по последней цифре учебного шифра студента в одной из двух таблиц в зависимости от того, четной или нечетной является предпоследняя цифра этого шифра), тексты условий задач для контрольной работы, тесты для самоконтроля. Рисунки, примеры решения задач и задачи контрольной работы имеют раздельную нумерацию. Теоретические сведения в сочетании с изучением примеров решения задач, приведенных в данном пособии, позволят самостоятельно применять законы и закономерности курса практически, в решении задач контрольной работы. Решение любой задачи целесообразно выполнять в следующем порядке: а) записать условие задачи, привести известные числовые данные к СИ; б) уяснить существо физического процесса; в) выяснить, какие законы следует использовать в решении задач; г) составить и решить уравнения в общем виде; д) выполнить подстановку числовых значений физических величин и вычисление искомой величины. Контрольная работа по дисциплине «Магнетизм и магнитные явления» должна быть написана чернилами в тетради или на листах формата А4. Условия задач следует переписывать полностью, без сокращений. Для замечаний рецензента необходимо оставить поля. Решение задачи должно сопровождаться пояснениями подобно тому, как это сделано в примерах решения. Для успешного овладения вопросами учебной программы при подготовки к зачету, выполнению контрольной работы кроме данного методического указания возможно использование литературы из библиографического списка.
Библиографический список 1. Трофимова Т.И. Курс общей физики, М. Высш. Школа.,1997 2. Волькенштейн В.С. Сборник задач по общему курсу физики, С.-Пб.: Книжный мир,2003. 3. Иродов И.Е. Основные законы электромагнетизма, М. Высшая школа, 1983. 4. Савельев И.В. Курс общей физики, ч.2. Электричество и магнетизм. М. Наука, 1988. 5. Калашников С.Г. Электричество. М. Наука, 1988 6. Яворский Б.М., Пинский А.А. Основы Физики, ч. 2. М. Наука, 1974. 7. Зисман Г.А., Тодес О.М. Курс общей физики, ч. 2. М. Наука 1995. 8. Зильберман Г.Е. Электричество и магнетизм. Уч. Пособие для втузов, 1970. Введение Атомы любого вещества состоят из заряженных частиц (положительно заряженных протонов и отрицательно заряженных электронов). Если на теле имеется избыток зарядов какого-либо знака, то тело заряжено, это тело кратко будем называть зарядом. Вокруг любого заряда возникает электрическое поле, которое воздействует на другие заряды. При движении зарядов, наряду с электрическим полем, вокруг заряда возникает магнитное поле. Магнитное поле порождается движущимися электрическими зарядами (токами) и действует на движущиеся электрические заряды (токи). Магнитных зарядов и магнитных токов нет. Электрическое и магнитное поля взаимосвязаны: переменное электрическое поле порождает магнитное поле, а переменное магнитное поле порождает электрическое поле (явление электромагнитной индукции). В пространстве электромагнитное поле распространяется в виде электромагнитных волн, это используется в радио, телевидении, сотовой связи, радиолокации. Свет – это тоже электромагнитные волны. Использование электромагнетизма играет ведущую роль во многих отраслях науки и техники. С электромагнетизмом связывают развитие энергетики, транспорта, вычислительной техники, физики плазмы, термоядерного синтеза. Магнитные разведка, дефектоскопия, магнитные линзы, магнитная обработка воды, поезда на магнитной подушке - вот далеко неполный перечень перспективных областей промышленного применения магнитного поля. Неотъемлемой частью компьютерного томографа, без которого невозможна современная медицинская диагностика, является также источник магнитного поля. В течение многих лет не ослабевает интерес к магнитным полям биологических объектов, повышено внимание к среде обитания их и к космосу, а также вопросам влияния магнитного поля Земли на человека. Магнитные явления были известны еще в древнем мире. Компас был изобретен более 4500 лет тому назад. Он появился в Европе приблизительно в XII веке новой эры. Однако только в XIX веке была обнаружена связь между электричеством и магнетизмом и возникло представление о магнитном поле. В настоящее время электромагнитные явления широко используются в электродвигателях, в получении, передаче и преобразовании электрической энергии и во всех отраслях техники. В связи с этим возник данный курс по изучению явлений магнетизма и электромагнитной индукции. В этом курсе изучаются основные разделы теории, а также задачи, имеющие практическое значение. Даны контрольные задания для студентов заочного отделения, необходимые для самостоятельного изучения данного курса. Приводятся примеры решения типичных задач, что поможет при выполнении контрольной работы. Все это позволяет добросовестному студенту самостоятельно освоить данный курс и использовать полученные знания в дальнейшем. Магнитные свойства вещества. Электромагнитная индукция. В 1831 году М.Фарадей открыл явление электромагнитной индукции, которое заключается в возникновении электрического тока в проводящем контуре, при изменении магнитного потока, пронизывающего этот контур. Возникающий ток называется индукционным (индукция – (с лат.) наведение). Закон электромагнитной индукции (закон Фарадея): ЭДС электромагнитной индукции в замкнутом контуре равна скорости изменения магнитного потока через поверхность, ограниченную этим контуром.
Если контур содержит N витков, то ЭДС индукции равна скорости изменения потокосцепления,
Знак «минус» в формулах 15 и 16 является математическим выражением правила Ленца, согласно которому, индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток.
Рис. 17. Применение правила Ленца. Направление индукционного тока определяется следующим образом: установить направление внешнего магнитного поля В, определить увеличивается или уменьшается поток вектора магнитной индукции внешнего поля, по правилу Ленца указать направление вектора магнитной индукции индукционного тока Вi., по правилу правого винта определить направление индукционного тока в контуре. На рис. 17 виток проводника помещен в неоднородное магнитное поле, созданное движущимся постоянным магнитом, так как индукция внешнего магнитного тока В нарастает, то вектора Согласно гипотезе Максвелла, природа ЭДС индукции заключается в возникновении вихревого электрического поля в любой области пространства, где существует переменное магнитное поле. Возникновение ЭДС индукции в движущемся проводнике объясняется действием силы Лоренца со стороны магнитного поля на движущиеся вместе с проводником электрические заряды. Пусть проводник длиной l перемещается со скоростью
где α – угол между вектором магнитной индукции и скоростью движения проводника.
Рис. 18. Возникновение ЭДС индукции в движущемся проводнике. Самоиндукция – это явление возникновения индукционного тока в замкнутом контуре при изменении силы тока в нем (частный случай электромагнитной индукции). При протекании в контуре тока I создается магнитное поле, характеризующееся магнитным потоком Ф.
где L - коэффициент самоиндукции или индуктивность контура, которая зависит от геометрической формы контура, его размеров и от среды, в которой он находится. Единицы измерения индуктивности в СИ Генри ЭДС самоиндукции пропорциональна скорости изменения силы тока в контуре.
Для катушки имеем
где L - коэффициент самоиндукции или индуктивность катушки, которая как и индуктивность контура зависит от геометрической формы контура, его размеров и от среды, в которой он находится. Индуктивность катушки определяется как коэффициент пропорциональности между потокосцеплением и силой тока в катушке: а при наличии сердечника с магнитной проницаемостью μ:
где μ0 – магнитная постоянная, В электрической цепи, содержащей индуктивность, при размыкании цепи сила тока изменяется по закону
А при замыкании цепи сила тока изменяется по закону
где I0 - максимальная сила тока, R - сопротивление цепи, L - индуктивность катушки, t - время процесса. Если два контура расположены один возле другого и в каждом из них изменяется сила тока, то они будут взаимно влиять друг на друга. Изменение в первом контуре вызовет появление индуцированной ЭДС во втором контуре и, наоборот, изменение тока и магнитного поля второго контура будет причиной появления индуцированной ЭДС в первом контуре. Это явление называется взаимоиндукцией, а ЭДС, возникающая вследствие влияния контуров друг на друга, называется ЭДС взаимоиндукции
где Lвз - коэффициент взаимной индукции. Явление электромагнитной индукции лежит в основе принципа действия многих инженерных устройств, таких как генератор переменного тока, трансформатор, поезд на магнитной подушке, детекторы металлов и так далее. Генератор переменного тока - устройство, преобразующее механическую энергию в электрическую энергию. В настоящее время имеется много типов индукционных генераторов, но все они состоят из одних и тех же основных частей. Это, во-первых, электромагнит или постоянный магнит, создающий магнитное поле, и, во-вторых, обмотка или рамка, в которой индуцируется переменная ЭДС. В некоторых генераторах (рис. 18 а) обмотка вращается вокруг горизонтальной или вертикальной оси. Поэтому он называется ротором. Неподвижный электромагнит называют статором. При этом угол между вектором индукции магнитного поля, созданного электромагнитом или постоянным магнитом, изменяется по закону В больших промышленных генераторах (рис. 18 б) вращается электромагнит, который является ротором, в то время как обмотки, в которых наводится ЭДС, уложены в пазах статора и остаются неподвижными. Дело в том, что подводить ток к ротору или отводить его из обмотки ротора во внешнюю цепь приходиться при помощи скользящих контактов. Для этого ротор снабжается контактными кольцами, присоединенными к концам его обмотки. Неподвижные пластины - щетки - прижаты к кольцам и осуществляют связь обмотки ротора с внешней цепью.
Рис. 19. Генераторы переменного тока.
Пример 15: В однородном магнитном поле, индукция которого В=0,1Тл, вращается катушка, состоящая из N=200 витков. Ось вращения катушки перпендикулярна к ее оси и к направлению магнитного поля. Период обращения катушки Т=0,2 с; площадь поперечного сечения S=4 см2. Найти максимальную ЭДС индукции εmax во вращающейся катушке. Дано: В =0,1 Тл, N =200, Т =0,2 с, S =4 см2 =4·10-4 м2 . Решение: Согласно закону Фарадея ЭДС индукции равна скорости изменения магнитного потока Тогда Вычисления:
Пример 16. Плоский проводящий контур с площадью S=50 см² помещен в однородное магнитное поле, индукция которого В=4 мТл. Сопротивление контура R=1 Ом. Плоскость контура составляет угол α=300 с линиями магнитной индукции. Определить величину заряда q, который пройдет по контуру при выключении магнитного поля. Дано: S= 50 см² =5·10-3 м², В= 4 мТл =0,004 Тл, R= 1 Ом, α= 30˚. Решение: Согласно определению сила тока равна величине заряда переносимого через данную площадь сечения в единицу времени, то есть
Искомое значение заряда Вычисляем
Пример 17. Горизонтальный стержень длиной l=1 м вращается вокруг вертикальной оси, проходящей через один из его концов. Ось вращения параллельно магнитному полю, индукция которого В=50 мкТл. При какой частоте вращения ν стержня разность потенциалов на концах этого стержня U=1 мВ? Дано: l =1 м, В =50 мкТл =5·10-5 Тл, U =1 мВ =10-3 В Решение: Разность потенциалов возникает за счет наведения в проводнике ЭДС индукции При вращении площадь, пересекаемая проводником пропорциональна углу поворота Получаем Искомая частота вращения Вычисление:
Пример 18. По соленоиду, содержащему N=600 витков, течет ток силой I=5 А. Длина соленоида l=40 см, площадь его сечения S=10 см², сердечник немагнитный. Определить среднее значение ЭДС εsср самоиндукции, которая возникает в соленоиде, если сила тока уменьшается практически до нуля за время Δt=0,4 мс после отключения соленоида от источника тока. Дано: N= 600, I0= 5 А, I= 0 А, l= 40 см= 0,4 м, S= 10 см² =10-3м2, Δt= 0,4 мс =4·10-4с Решение: ЭДС самоиндукции определяется по формуле Среднее значение ЭДС самоиндукции где
Получаем Вычисления:
Пример 19: Источник тока замкнут на катушку с индуктивностью L=0,4 Гн. Определить сопротивление R катушки, если сила I тока в катушке достигает 20 % ее максимального значения за время t=0,1 с после замыкания цепи. Дано: L= 0,4 Гн, I= 0,2 I0, t= 0,1 с. Решение: При замыкании цепи сила тока определяется по формуле
Искомое сопротивление Вычисление: Магнитные цепи. Магнитная цепь – это совокупность тел, внутри которой проходят замкнутые линии магнитной индукции. Магнитная цепь (рис. 20) включает в себя систему ферромагнитных тел (магнитопровод), которые предназначены для усиления и направления магнитного поля и обмотки с током, в которой это магнитное поле и создается.
Рис. 20
Неразветвленной магнитной цепью называют цепь, в каждой точке которой магнитный поток постоянен (Ф =const). Рассмотрим неразветвленную магнитную цепь, которая состоит из магнитопровода длиной l, изготовленного из ферромагнитного материала с магнитной проницаемостью m1. В магнитопроводе имеется воздушный зазор (m2 =1) длиной δ. Площадь поперечного сечения и магнитопровода и зазора – S. По обмотке, содержащей N витков, течет ток силой I.
Рис. 21
Основным законом, используемым при расчетах магнитных цепей, является теорема и циркуляции вектора напряженности магнитного поля или закон полного тока (формула (32)). Запишем закон полного тока для данной цепи: Произведение силы тока в обмотке на число витков этой обмотки принято называть магнитодвижущей силой (МДС):
МДС вызывает в магнитной цепи магнитный поток подобно тому, как ЭДС вызывает ток в электрической цепи. Получаем выражение: По аналогии с сопротивлением электрическому току часто используют сопротивление магнитному потоку, называемое магнитным сопротивлением. Магнитным сопротивлением называется выражение Получаем выражение, аналогичное закону Ома для электрической цепи
Магнитный поток, являясь аналогом силы тока в неразветвленной электрической цепи, пропорционален магнитодвижущей силе и обратно пропорционален магнитному сопротивлению. При расчете неразветвленной магнитной цепи следует использовать следующий алгоритм: 1 вариант.Определение МДС по заданному магнитному потоку (прямая задача). 1) Выделить в магнитной цепи однородные участки с площадями сечений s1, s2,..., sk,...; и средними длинами l1, l2,..., lk. 2) По заданному магнитному потоку и сечениям участков определить магнитные индукции B1, B2,..., Bk. 3) По таблице зависимости B (H) определить напряженности на участках магнитопровода H1, H2,..., Hk. Для воздушного участка напряженность полярассчитывается по формуле 4) По закону полного тока рассчитать МДС обмотки. 2 вариант. Определение магнитного потока по заданной МДС (обратная задача). 1) Магнитную цепь представить совокупностью однородных участков с площадями поперечных сечений s1, s2,..., sk,...; и средними длинами l1, l2,..., lk. 2) Произвольно выбрав магнитную индукцию для одного из участков, определить магнитную индукцию на других участках. Для этого используют зависимость B1s1=B2s2=B3s3=...=Ф. 3) По таблице зависимости В(Н) определить напряженности магнитного поля для всех участков цепи. 4) Определить произведения напряженностей магнитного поля на соответствующую длину участков цепи H1l1, H2l2,..., Hklk. Просуммировать найденные выражения, построить график зависимости магнитного потока от МДС. 5) Для заданной МДС определить магнитный поток Ф и магнитные индукции B на участках цепи. Для разветвленных магнитных цепей (рис. 22) справедливы законы Кирхгофа. Первый закон Кирхгофа – алгебраическая сумма магнитных потоков в узле равна нулю.
при этом магнитный поток, входящий в узел считается положительным, а выходящий из него отрицательным (узел – это место магнитной цепи, в которой сходятся не менее 3 магнитных потоков).
Рис. 22
Второй закон Кирхгофа – алгебраическая сумма МДС в замкнутом контуре равна алгебраической сумме произведений магнитных потоков на соответствующее магнитное сопротивление участков.
Электромагниты. Электромагнит - электротехническое устройство, состоящее из ферромагнитного сердечника с токопроводящей обмоткой, которая при включении в электрическую цепь намагничивает сердечник. Электромагнит используют для создания магнитных потоков в электрических машинах и аппаратах, устройствах автоматики. Большинство технических применений магнитов основывается на их способности притягивать и удерживать ферромагнитные предметы. Электромагнит состоит из обмотки и ферромагнитного сердечника, который приобретает свойства магнита при прохождении по обмотке тока (рис. 23).
Рис. 23 Основной характеристикой электромагнита является его подъемная сила - сила, с которой электромагнит удерживает ферромагнитный предмет, расположенный в непосредственной близости к нему:
где µ0 - магнитная постоянная, S – площадь прилипания предмета к сердечнику, B – индукция магнитного поля электромагнита.
Пример 20: Каким должен быть намагничивающий ток катушки, имеющей N=200 витков, чтобы получить в тороиде, изготовленном из стали Э41 магнитный поток Ф=0,157мВб? Средний радиус r=5 см, а диаметр сечения тороида d=2 см.
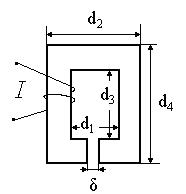
Дано: N=200, Ф=0,157мВб=1,57·10-4Вб, r=5 см=0,05м, d=2 см=0,02м. Решение: Данная цепь является неразветвленной, поэтому магнитный поток Ф одинаков во всех сечениях цепи. Так как площадь сечения S одинакова в разных частях магнитопровода, то и магнитная индукция B одинакова во всех участках цепи и равна Подставляем численные значения: Находим магнитную индукцию по формуле: Запишем закон полного тока для напряженности магнитного поля для данной магнитной цепи: l – длина средней линии магнитопровода, определяется по формуле: Вычисляем численное значение Искомое значение силы тока: Рассчитаем конечный результат: Пример 21. Замкнутая магнитная цепь, имеющая размеры d1=6 см, d2=14см, d3=7 см, d4=15 см, набрана из стали Э41 толщиной h=4 см. Зазор имеет ширину δ=0,5 мм. Сколько витков обмотки должна иметь катушка с током I=0,5 А, чтобы создать в магнитопроводе поток Ф=1,6 мВб?
Дано: d1=6см=0,06м, d2=14см=0,14м, d3=7см=0,07м, d4=15см=0,015м, h=4см=0,04м, δ=0,5мм=0,0005м, I=0,5 А, Ф=1,6мВб=1,6·10-3Вб. Решение: Данная цепь является неразветвленной цепью, поэтому магнитный поток Ф одинаков во всех сечениях цепи. Так как площадь сечения S одинакова в разных частях магнитопровода, то и магнитная индукция B одинакова во всех участках цепи и равна Подставляем численные значения:
Находим магнитную индукцию: Запишем закон полного тока для напряженности магнитного поля для данной магнитной цепи: где Н1 – напряженность магнитного поля в магнитопроводе, которая определяется по таблице зависимости В от Н для стали Э41. При В =1 Тл напряженность Н1 =300 А/м, l – длина средней линии магнитопровода, определяется по формуле: Находим искомое число витков: Рассчитаем конечный результат:
Пример 22. При каком магнитодвижущей силе в обмотке, число витков которой равно N=300, магнитный поток в магнитопроводе, изготовленном из стали Э41, будет равен Ф=1,2 мВб. Магнитопровод имеет размеры d1=20 см, d2=30см, d3=8 см, d4=6 см, толщина стали в пакете h=5 см.
Дано: N=300, Ф=1,2мВб=1,2·10-3Вб, d1=20см=0,2м, d2=30см=0,3м, d3=8см=0,08м, d4=6 см=0,06м, h=5 см=0,05м. Решение: Данная цепь является неразветвленной, поэтому магнитный поток Ф одинаков во всех сечениях цепи. Площадь сечения S в разных частях магнитопровода неодинакова, и магнитная индукция B неодинакова во всех участках цепи и равна Подставляем численные значения:
Находим магнитную индукцию: Запишем закон полного тока для напряженности магнитного поля для данной магнитной цепи: l1 – длина средней линии магнитопровода с шириной d3, определяется по формуле: l2 – длина средней линии магнитопровода с шириной d4, определяется по формуле: Вычисляем численное значение Находим искомое значение МДС:
Пример 23. Определить магнитный поток внутри кольца при токе в обмотке I=0,4 А. Размеры кольца d1=7 см, d2=5 см, толщина стали Э41 в пакете h=3 см. Число витков в обмотке N=600.
Дано: I=0,4 А, d1=7см=0,07м, d2=5см=0,05м, h=3 см=0,03м, N=600. Решение: Данная цепь является неразветвленной, поэтому магнитный поток Ф одинаков во всех сечениях цепи. Так как площадь сечения S одинакова в разных частях магнитопровода, то и магнитный поток равен Подставляем численные значения:
Запишем закон полного тока для напряженности магнитного поля для данной магнитной цепи:
Находим искомое значение напряженности магнитного поля: Рассчитаем конечный результат:
Пример 24. Определить магнитный поток в кольце с зазором δ=1мм при токе в обмотке I=0,4 А. Размеры кольца d1=16 см, d2=12 см, толщина стали Э41 в пакете h=3 см. Число витков в обмотке N=700.
Дано: δ=1мм=0,001м, I=0,4 А, d1=16 см=0,16м, d2=12 см=0,12м, h=3 см=0,03м, N=700. Решение: Данная цепь является неразветвленной, поэтому магнитный поток Ф одинаков во всех сечениях цепи. Так как площадь сечения S одинакова в разных частях магнитопровода, то и магнитная индукция B одинакова во всех участках цепи. Запишем закон полного тока для напряженности магнитного поля для данной магнитной цепи: Вычисляем численное значение Получим зависимость напряженности магнитного поля в магнитопроводе от индукции магнитного поля: В системе координат ВОН строим графики зависимости В от Н согласно полученной формуле и согласно таблице зависимости В от Н для стали Э41. Магнитная индукция точки пересечения этих двух графиков есть значение индукции магнитного поля для данной магнитной цепи. График зависимость В от Н представляет прямую зависимость, для ее построения достаточно двух точек: 1) при Н=0 2) п
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 535; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |

 (33)
(33) (34)
(34)
 и
и 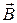 антипараллельны.
антипараллельны. в однородном магнитном поле с индукцией
в однородном магнитном поле с индукцией  (35)
(35)
 , (36)
, (36)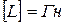 .
. (37)
(37) , (38)
, (38) . С учетом формулы (22) получим индуктивность соленоида при отсутствии сердечника:
. С учетом формулы (22) получим индуктивность соленоида при отсутствии сердечника:  ,
, (39)
(39) – число витков, приходящееся на единицу длины соленоида,
– число витков, приходящееся на единицу длины соленоида,  - объем соленоида, S – площадь сечения.
- объем соленоида, S – площадь сечения. , (40)
, (40) , (41)
, (41) , (42)
, (42) , где
, где  -циклическая частота,
-циклическая частота, 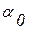 - начальная фаза вращения. Согласно закону Фарадея ЭДС индукции равна скорости изменения полного магнитного потока
- начальная фаза вращения. Согласно закону Фарадея ЭДС индукции равна скорости изменения полного магнитного потока  .
.  - полный магнитный поток, пронизывающий обмотку, состоящую из N витков. Тогда
- полный магнитный поток, пронизывающий обмотку, состоящую из N витков. Тогда  .
.
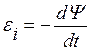 .
.  - полный магнитный поток, пронизывающий катушку (потокосцепление), где
- полный магнитный поток, пронизывающий катушку (потокосцепление), где  - угол между векторами магнитной индукции и нормалью, проведенной к контуру, при вращении рамки в магнитном поле угол изменяется по формуле
- угол между векторами магнитной индукции и нормалью, проведенной к контуру, при вращении рамки в магнитном поле угол изменяется по формуле  ,
,  -циклическая частота,
-циклическая частота,  , максимальная ЭДС равна
, максимальная ЭДС равна  .
.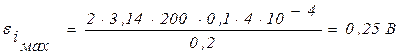 .
. . Согласно закону Ома сила тока равна
. Согласно закону Ома сила тока равна 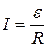 . Согласно закону Фарадея ЭДС индукции равна скорости изменения магнитного потока
. Согласно закону Фарадея ЭДС индукции равна скорости изменения магнитного потока  или
или  . Чтобы найти искомое количество заряда проинтегрируем последнее выражение
. Чтобы найти искомое количество заряда проинтегрируем последнее выражение  .
. - магнитный поток, пронизывающий контур при включенном поле, где- угол между векторами магнитной индукции и нормалью, проведенной к контуру,
- магнитный поток, пронизывающий контур при включенном поле, где- угол между векторами магнитной индукции и нормалью, проведенной к контуру,  .
. - магнитный поток, пронизывающий контур при выключенном поле, так как
- магнитный поток, пронизывающий контур при выключенном поле, так как  , то
, то  .
. .
. Кл.
Кл. , где Ф – магнитный поток, пересекаемый проводником при движении,
, где Ф – магнитный поток, пересекаемый проводником при движении,  , α =0, так как
, α =0, так как  плоскости вращения, тогда
плоскости вращения, тогда 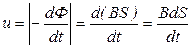 .
. , где
, где  - радиус описываемой окружности.
- радиус описываемой окружности. , так как
, так как  - угловая скорость, то получаем
- угловая скорость, то получаем  .
. .
. (Гц)
(Гц) , где
, где  скорость изменения силы тока в соленоиде.
скорость изменения силы тока в соленоиде. ,
, - индуктивность соленоида, где μ0=1,26·10-6 Гн/м – магнитная постоянная, μ – магнитная проницаемость среды, так как сердечник немагнитный μ =1,
- индуктивность соленоида, где μ0=1,26·10-6 Гн/м – магнитная постоянная, μ – магнитная проницаемость среды, так как сердечник немагнитный μ =1,  - объем соленоида. Тогда
- объем соленоида. Тогда  .
. - изменение силы тока (
- изменение силы тока ( А,
А, 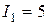 А)
А) .
. .
. , где
, где  , тогда
, тогда 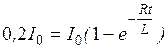 или
или  , получаем
, получаем  =1,25или
=1,25или  .
. .
. Ом.
Ом.

 , где Н1 – напряженность магнитного поля в магнитопроводе
, где Н1 – напряженность магнитного поля в магнитопроводе  , Н2 – напряженность магнитного поля в зазоре
, Н2 – напряженность магнитного поля в зазоре  , где Ф – магнитный поток, пронизывающий магнитную цепь, l – длина средней линии магнитопровода.
, где Ф – магнитный поток, пронизывающий магнитную цепь, l – длина средней линии магнитопровода. . (43)
. (43) или
или 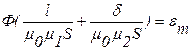 .
. . Очевидно, что магнитное сопротивление как и электрическое пропорционально длине магнитопровода и обратно пропорционально его сечению. Тогда обозначим через
. Очевидно, что магнитное сопротивление как и электрическое пропорционально длине магнитопровода и обратно пропорционально его сечению. Тогда обозначим через 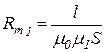 - сопротивление магнитопровода, а через
- сопротивление магнитопровода, а через  - сопротивление воздушного зазора. Выражение
- сопротивление воздушного зазора. Выражение  - полное сопротивление рассматриваемой магнитной цепи.
- полное сопротивление рассматриваемой магнитной цепи. . (44)
. (44) , где μ0 =1,26·10-6 Гн/м – магнитная постоянная
, где μ0 =1,26·10-6 Гн/м – магнитная постоянная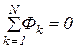 , (45)
, (45)
 , (46)
, (46)
 , (47)
, (47)
 , где
, где 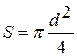 - площадь сечения тороида.
- площадь сечения тороида. .
.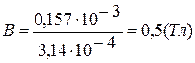
 , где Н – напряженность магнитного поля в магнитопроводе, которая определяется по таблице зависимости В от Н для стали Э41. При В =0,5 Тл напряженность Н =85 А/м.
, где Н – напряженность магнитного поля в магнитопроводе, которая определяется по таблице зависимости В от Н для стали Э41. При В =0,5 Тл напряженность Н =85 А/м. .
.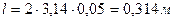 .
. .
.
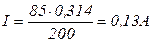 .
.
 , где S – площадь сечения магнитопровода,
, где S – площадь сечения магнитопровода,  .
.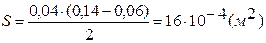 .
. .
. ,
,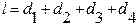 . Вычисляем численное значение
. Вычисляем численное значение  . Н2 – напряженность магнитного поля в воздушном зазоре, которая определяется по формуле:
. Н2 – напряженность магнитного поля в воздушном зазоре, которая определяется по формуле: 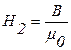 , где μ0 =1,26·10-6 Гн/м – магнитная постоянная. Получаем
, где μ0 =1,26·10-6 Гн/м – магнитная постоянная. Получаем  А/м.
А/м. .
. .
.
 , где i=1,2, где
, где i=1,2, где  и
и 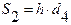 .
.
 .
. и
и 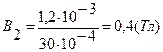 .
. , где Н1 – напряженность магнитного поля в магнитопроводе с шириной d3, Н2 – напряженность магнитного поля в магнитопроводе с шириной d4, которые определяются по таблице зависимости В от Н для стали Э41. При В1 =0,3 Тл напряженность Н1 =60 А/м, при В2 =0,4 Тл напряженность Н2 =70 А/м.
, где Н1 – напряженность магнитного поля в магнитопроводе с шириной d3, Н2 – напряженность магнитного поля в магнитопроводе с шириной d4, которые определяются по таблице зависимости В от Н для стали Э41. При В1 =0,3 Тл напряженность Н1 =60 А/м, при В2 =0,4 Тл напряженность Н2 =70 А/м. . Вычисляем численное значение
. Вычисляем численное значение  .
. .
. .
. А.
А.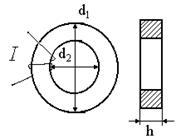
 , где
, где 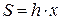 , где как видно из рисунка
, где как видно из рисунка  .
. (м),
(м),  .
. , где Н – напряженность магнитного поля в магнитопроводе, l – длина средней линии магнитопровода, определяется по формуле:
, где Н – напряженность магнитного поля в магнитопроводе, l – длина средней линии магнитопровода, определяется по формуле: ,
,  .
. ,
,  А/м. По таблице зависимости В от Н для стали Э41 при Н =1277 А/м В =1,4 Тл.
А/м. По таблице зависимости В от Н для стали Э41 при Н =1277 А/м В =1,4 Тл. Вб.
Вб.
 , где
, где  - магнитодвижущая сила, равная
- магнитодвижущая сила, равная  =0,4·700=280 А, Н1 – напряженность магнитного поля в магнитопроводе, Н2 – напряженность магнитного поля в воздушном зазоре, определяется по формуле
=0,4·700=280 А, Н1 – напряженность магнитного поля в магнитопроводе, Н2 – напряженность магнитного поля в воздушном зазоре, определяется по формуле  , где μ0 =1,26·10-6 Гн/м – магнитная постоянная, l1 – длина средней линии магнитопровода, определяется по формуле:
, где μ0 =1,26·10-6 Гн/м – магнитная постоянная, l1 – длина средней линии магнитопровода, определяется по формуле:  , δ – длина воздушного зазора.
, δ – длина воздушного зазора. .
.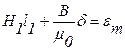 .
. ,
,


