
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон Био-Савара-Лапласа в вакууме.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г.). Совместно с Лапласом они пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется принципу суперпозиции: Если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности.
Индукцию проводника с током
Закон Био–Савара-Лапласа определяет индукцию магнитного поля, создаваемого малым участком
где
Рис.6
Пример 1. Найти индукцию магнитного поля в точке, отстоящей на расстоянии 10 см от бесконечно длинного проводника, по которому течет ток силой 5 А. Дано:
где
По правилу буравчика определим направление Из рисунка видно
где α1, α2 –углы между направлением тока в проводнике и радиусами – векторами, проведенными от концов проводника в точку А. Если проводник бесконечно длинный, то α1=00, cosα1=1, α2=1800, cosα2=-1. Тогда
Вычисления:
Выведенная в примере 1 формула:
позволяет определить магнитную индукцию поля прямого бесконечно длинного проводника с током.
Пример 2. По прямому проводнику длиной 4 м течет ток I=100 А. Определить индукцию В магнитного поля в точке, равноудаленной от концов проводника и находящейся на расстоянии 1 м от него. Дано: Решение: Разобьем проводник на элементарные отрезки
По правилу буравчика определим направление Из рисунка видно
где α1, α2 –углы между направлением тока в проводнике и радиусами – векторами, проведенными от концов проводника в точку А. Как видно из рисунка cos α 1=-cos α 2= тогда Вычисления:
Выведенная в примере 2 формула:
позволяет определить магнитную индукцию поля прямого проводника с током конечной длины. Пример 3. Из проводника длиной l=3,14 м сделано кольцо. Определить индукцию В магнитного поля в точке, лежащей в центре кольца, если сила тока в проводнике равна 5 А. Дано: Решение: Разобьем проводник на элементарные отрезки
По правилу буравчика определим направление
Из рисунка видно, что Радиус кольца Производим расчет
Выведенная в примере 3 формула:
позволяет определить магнитную индукцию поля в центре кругового проводника с током.
Пример 4. Индукция В магнитного поля в точке, лежащей на оси проводящего кольца на расстоянии b=0,6 м от плоскости кольца, равна 50 мкТл. Определить силу тока в кольце. Радиус кольца R=0,8 м. Дано:
По правилу буравчика определим направление Тогда Из рисунка видно, что С учетом этого получаем
Отсюда искомая сила тока в кольце. Тогда
Выведенная в примере 4 формула:
позволяет определить магнитную индукцию поля на оси проводящего кольца. Пример 5. Два длинных прямых параллельных проводника с одинаково направленными токами I1=2 A и I2=4 A расположены на расстоянии r=10 см друг от друга. Определить индукцию магнитного поля в точке, лежащей в середине отрезка прямой, соединяющего проводники. Дано: Решение: Согласно принципу суперпозиции (формула 1) индукция магнитного поля в точке А равна
где
Получаем где μ0=1,26·10-6 Подставим числовые значения:
Пример 6. Два прямолинейных бесконечно длинных проводника скрещены под прямым углом. По проводам текут токи силами 80 А и 60 А. Расстояние между проводниками 10 см. Определить магнитную индукцию в точке А, одинаково удаленной от обоих проводников. Дано: Решение: Согласно принципу суперпозиции (формула 1) индукция магнитного поля в точке А равна
где
Получаем Вычисление:
|
|||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.72.55 (0.008 с.) |

 (1)
(1) можно представить как векторную сумму элементарных индукций
можно представить как векторную сумму элементарных индукций  , создаваемых отдельными участками проводника длиной l.
, создаваемых отдельными участками проводника длиной l. (2)
(2) проводника с током I:
проводника с током I: , (3)
, (3) – магнитная постоянная,
– магнитная постоянная, - радиус-вектор, проведенный от элемента проводника
- радиус-вектор, проведенный от элемента проводника  , имеющего направление тока в проводнике, к точке, в которой определяется индукция магнитного поля (рис.6).
, имеющего направление тока в проводнике, к точке, в которой определяется индукция магнитного поля (рис.6).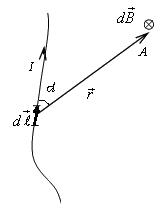
 ;
;  .
. Решение: Разобьем проводник на элементарные отрезки
Решение: Разобьем проводник на элементарные отрезки 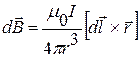 ,
, ). По принципу суперпозиции магнитная индукция
). По принципу суперпозиции магнитная индукция 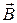 равна сумме магнитных индукций
равна сумме магнитных индукций  имеют одинаковые направления, поэтому можно заметить векторное интегрирование скалярным:
имеют одинаковые направления, поэтому можно заметить векторное интегрирование скалярным:  , где
, где  , где α – угол между элементом
, где α – угол между элементом  и радиус-вектором
и радиус-вектором  .
. , где
, где 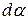 - угол, лежащий против элемента проводника с током
- угол, лежащий против элемента проводника с током  , где
, где  . Тогда
. Тогда  . С учетом этого получаем
. С учетом этого получаем ,
,
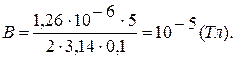
 ;
;  ;
; 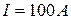 .
.
 .
.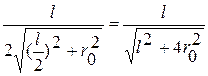 ,
, .
.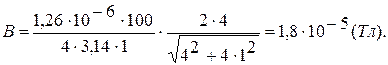
 (5)
(5) ;
;  .
.
 , где
, где  – магнитная постоянная,
– магнитная постоянная,  (интегрирование ведется по длине кругового проводника l). В нашем случае
(интегрирование ведется по длине кругового проводника l). В нашем случае  , где
, где  , где α – угол между элементом
, где α – угол между элементом  , так как
, так как 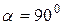 ,
,  , где R – радиус кольца. С учетом этого получаем
, где R – радиус кольца. С учетом этого получаем  .
. , тогда
, тогда 
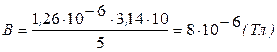 .
. (6)
(6) ;
;  ;
; 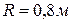
 Решение: Разобьем проводящее кольцо на элементарные отрезки
Решение: Разобьем проводящее кольцо на элементарные отрезки  - перпендикулярную плоскости кольца и
- перпендикулярную плоскости кольца и  - параллельную плоскости кольца, то есть
- параллельную плоскости кольца, то есть  .
. . Заметим, что
. Заметим, что  из соображений симметрии и что векторы
из соображений симметрии и что векторы  от различных элементов
от различных элементов  , где
, где  , где
, где  ,
, 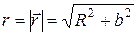 , где R – радиус кольца, b – расстояние от плоскости кольца до точки А.
, где R – радиус кольца, b – расстояние от плоскости кольца до точки А.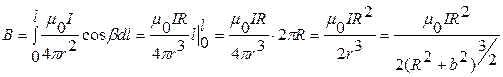 .
.
 .
. (7)
(7) ;
;  ;
;  ;.
;.  .
. , где
, где  - индукция магнитного поля, созданного в точке А проводником с током I1,
- индукция магнитного поля, созданного в точке А проводником с током I1,  - индукция магнитного поля, созданного в точке А проводником с током I2.
- индукция магнитного поля, созданного в точке А проводником с током I2. Определим направления векторов магнитной индукции в точке А по правилу буравчика. Как видно из рисунка
Определим направления векторов магнитной индукции в точке А по правилу буравчика. Как видно из рисунка  , поэтому модульное значение индукции магнитного поля в точке А
, поэтому модульное значение индукции магнитного поля в точке А  ,
, - индукция магнитного поля, созданного в точке А бесконечно длинным проводником с током I1 (формула 4),
- индукция магнитного поля, созданного в точке А бесконечно длинным проводником с током I1 (формула 4), - индукция магнитного поля, созданного в точке А бесконечно длинным проводником с током I2 (формула 4).
- индукция магнитного поля, созданного в точке А бесконечно длинным проводником с током I2 (формула 4). ,
, – магнитная постоянная.
– магнитная постоянная. (Тл).
(Тл). ;
;  ;
;  Определим направления векторов магнитной индукции в точке А по правилу буравчика. Как видно из рисунка
Определим направления векторов магнитной индукции в точке А по правилу буравчика. Как видно из рисунка  , поэтому модульное значение индукции магнитного поля в точке А
, поэтому модульное значение индукции магнитного поля в точке А  ,
, .
.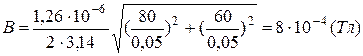 .
.


