
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 14. Диамагнетизм атомов и электронов проводимости. Магнитные свойства полупроводников.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
На прошлой лекции мы отметили, что существуют вещества диамагнитные, для которых магнитная восприимчивость Рассмотрим вначале отдельный атом с Z электронами, помещенный во внешнее магнитное поле
называемой ларморовской частотой.Если смотреть в направлении оси z (т.е. поля
Так как
где
Диамагнитная восприимчивость газа таких атомов
где Величина Если атом обладает постоянным магнитным моментом, равным магнетону Бора, то парамагнитная восприимчивость
где один множитель Так как На первый взгляд аналогичный расчет возможен и для свободных электронов (электронов проводимости). Под действием магнитного поля свободный электрон, обладающий скоростью
где
- так называемая циклотронная частота, равная
где мы исключили
Это выражение не может быть верным, так как оно не зависит от координаты электрона и обратно пропорционально Покажем в общем виде, что диамагнитная восприимчивость идеального электронного газа, подчиняющегося классической статистике, равна нулю. Направим декартову ось z в направлении магнитного поля
Функция Гамильтона для электрона в магнитном поле есть
где Свободная энергия идеального газа, подчиняющегося классической статистике, равна
где статистический интеграл
Здесь H – функция Гамильтона для одной частицы, N – их число. Для электронов проводимости функция Гамильтона H равна (15).Статистический интеграл Z равен произведению N одинаковых шестикратных интегралов, так как все N электронов независимы и тождественны. Заменим переменные интегрирования
При этом Совершенно аналогично можно показать, что диамагнитная восприимчивость, подчиняющаяся статистике Ферми, тоже равна нулю. Таким образом, при квазиклассическом рассмотрении электронный газ не обладает диамагнетизмом. Может возникнуть вопрос, не находится ли этот результат с не равным нулю диамагнетизмом атомов (5). На самом деле (5) получено на основании существенно квантового предположении о стационарных состояниях электронов в атоме, не подчиняющихся классической статистике. Ландау показал, что при квантовомеханическом рассмотрении движения свободных электронов в магнитном поле их диамагнитная восприимчивость равна 1/3 парамагнитной восприимчивости. Этот факт не противоречит предыдущему выводу, так как он связан с квантованием движения свободного электрона в магнитном поле – квантовании Ландау. Рассмотрим подробно, как на магнитных свойствах газа сказывается квантование Ландау. Т.е. посмотрим, что будет, если мы учтем вклад Как говорилось на прошлой лекции, в этом случае при выборе векторного потенциала в виде
и
Обращаю внимание, что одноэлектронные уровни энергии вырождены по квантовому числу
Таким образом, область допустимых значений
Для того, чтобы лучше была видна роль квантования Ландау, забудем пока о взаимодействии собственного магнитного момента с магнитным полем. В таком случае одноэлектронные уровни энергии приобретают вид
Одночастичные волновые функции остаются теми же самыми. В этом предположении энергии одноэлектронных состояний вырождены по спиновому квантовому числу. Согласно общему алгоритму нам нужно найти плотность одноэлектронных стационарных состояний
Поскольку в нашем предположении однончастичные энергии вырождены по спиновому квантовому числу, то
Поскольку однончастичные энергии также вырождены и по квантовому числу
Используя аппроксимацию суммы по волновым векторам интегралом, а также то обстоятельством, что область допустимых значений
Вычисляем интеграл по
Здесь введено обозначение
Это интеграл с дельта-функцией. Поэтому он вычисляется достаточно легко. Для того, чтобы его посчитать нужно сделать замену переменной, которая приводит этот интеграл к виду Однако здесь имеется тонкий момент. Этот момент связан с тем, что аргумент дельта-функции обращается в нуль в двух точках. Аргумент дельта-функции обращается в нуль в точке
Поскольку области интегрирования в (155) симметричны, а подынтегральная функция является четной, то в первом интеграле логично сделать замену переменной
Теперь для того, чтобы привести наш интеграл к нужному виду и воспользоваться основным свойством дельта-функции, следует, очевидно, сделать замену переменной
Согласно основному свойству дельта-функции
Здесь Таким образом, плотность одночастичных стационарных состояний
Свободная энергия идеального электронного газа
Подставляем плотность одночастичных состояний.
Здесь
В
Делаем обезразмеривабщую замену переменной. В нашем случае характерной энергией является энергия Ландау
Введем безразмерный химический потенциал
и безразмерную температуру
Тогда
Еще раз интегрируем по частям.
Таким образом, свободная энергия нашего газа
Таким образом, свободная энергия нашего газа
где
При данном х в сумме
где Сумму
Таким образом, наша задача состоит в том, чтобы представить сумму Прежде всего
где Таким образом,
Заменяем в сумме
Введем функцию
Тогда
Используя формулу Пуассона (194), получаем
Имея ввиду дальнейшее приложение нашей теории к описанию магнитных свойств электронного газа в металле, рассмотрим случай, когда наш газ сильно вырожден, т.е. когда Проведя стандартный анализ функции Рассмотрим важный с точки зрения практических приложений случай, когда
Проведем преобразование выражения
Преобразуем экспоненту
Таким образом,
Воспользовавшись тем, что
Вычисляем интеграл
В оставшемся интеграле делаем замену переменной
Учтя, что
Таким образом,
где
-специальная функция – интеграл Френеля второго рода. При получении (61) также было учтено, что у нас x>>1, и, поэтому мы можем заменить Аналогичным образом вычисляем интеграл
В оставшемся интеграле делаем замену переменной
. Таким образом,
где
-специальная функция – интеграл Френеля первого рода. При получении (63) также было учтено, что у нас x>>1, и, поэтому мы можем заменить Подставляя (61) и (62) в (58), получаем
Подставляем (65) в (57).
Вычисляем сумму
где
Интеграл (69) равен нулю, поскольку подынтегральная функция – нечетная, а пределы интегрирования – антисимметричны. Вычисляем коэффициент разложения
Рассмотрим случай
Итак, при
В случае n=0
Таким образом, имеем
Положим в (216) x=0. В результате получим
Отсюда искомая сумма
Подставляя (218) в (210), получаем
Итак,
Подставляя (75) в (47), получаем следующее выражение для свободной энергии нашего электронного газа
Итак, нам нужно вычислить интеграл
где Поступаем так же, как делали при вычислении химического потенциала и теплоемкости в отсутствие внешних силовых полей. Переходим к новой переменной интегрирования
Из-за наличия экспоненты в числителе и знаменателе подынтегральной функции основной вклад в этот интеграл дают |y|<~1. В области Таким образом, в указанных приближениях получаем
Произведя замену переменной
Подставляя полученный результат в выражение (77), находим
Подставляя (41) и (78), получаем
Итак, в указанных приближениях получаем следующее выражение для первого вклада в свободную энергию нашего электронного газа
Перейдем теперь к рассмотрению второго вклада В том случае, если в эту окрестность попадает много периодов осцилляции, т.е. если Таким образом, в случае, когда
Зная свободную энергию, мы можем легко найти любой внутренний параметр системы: ее энтропию, внутреннюю энергию и все обобщенные силы. Обобщенная сила
Элементарная работа, совершаемая системой при изменении внешнего параметра
Напряженность магнитного поля в нашей задаче является внешним параметром. Найдем обобщенную силу, отвечающую этому внешнему параметру. Для этого нам нужно вспомнить выражение для работы, совершаемой изотропной системой с магнитным моментом
Здесь M – проекция магнитного момента на направление магнитного поля. Следовательно, обобщенная сила, отвечающая модулю напряженности магнитного поля, есть проекция среднего магнитного момента нашего газа на направление магнитного поля. Таким образом, проекция среднего магнитного момента нашего газа на направление магнитного поля есть
В свою очередь магнитная восприимчивость нашего электронного газа по определению есть
Объединяя вместе две формулы, получаем, что
Итак, для того, чтобы найти магнитный момент и магнитную восприимчивость нашего электронного газа, нам нужно дифференцировать выражение (87) для свободной энергии по величине магнитного поля. При дифференцировании свободной энергии возникает естественный вопрос, а нужно ли учитывать зависимость химического потенциала от магнитного поля? То нужно это делать или нет, естественно, определяется той точностью, с которой мы производим наш расчет. Как уже было оговорено, мы вычисляем свободную энергию с точностью до первой неисчезающей поправки по магнитному полю. Напомню, что мы рассматриваем случай малых магнитных полей, когда
Определим, какой степени магнитного поля пропорциональна эта поправка. Это, конечно же, можно сделать, решив с нужной точностью уравнение для химического потенциала. Однако здесь можно поступить гораздо проще. Наш газ представляет собой изотропную систему. Поэтому никакие скалярные физические характеристики нашего газа не зависят от направления магнитного поля. В том числе, не зависит от направления магнитного поля и химический потенциал. Поэтому поправка По своему определению химический потенциал есть истинный скаляр. Напряженность магнитного поля является аксиальным вектором. Модуль же аксиального вектора истинным скаляром не является, истинным скаляром является только квадрат этого вектора. Поэтому поправка Подставляем (94) в наше выражение (87) для свободной энергии. Поскольку
Как известно, в состоянии равновесия
Таким образом, наше выражение для свободной энергии принимает вид
Поскольку поправка
Таким образом, в наших приближениях магнитная восприимчивость единицы объема
Итак, мы видим, что Пренебрегая малым (при
Мы рассмотрели случай, когда В случае же, когда
Следовательно, осцилляции с магнитным полем будут наблюдаться и во всех термодинамических характеристиках нашего электронного газа. В частности, осцилляцилирующие члены появляются и в магнитной восприимчивости. Подобные осцилляции магнитной восприимчивости были впервые экспериментально обнаружены у висмута и получили название эффекта де-Гааза – ван-Альфена, по имени ученых открывших это явление. Рассмотрим теперь диамагнитную восприимчивость невырожденных электронов проводимости полупроводника. Выражение (47) для свободной энергии остается, конечно, верным, однако в этом случае оно может быть упрощено: функция распределения Ферми может быть заменена распределением Больцмана
Перейдя к новой переменной интегрирования
Интеграл
Сумма членов бесконечно убывающей геометрической прогрессии
Таким образом,
Здесь мы ввели обозначение
Как видно, если не учитывать слабой зависимости химического потенциала от магнитного поля, то зависимость свободной энергии от В, определяется квадратной скобкой в (105). В случае невырожденных полупроводников, предельный случай Разлагая в (105) квадратную скобку в ряд по z с точностью до второго порядка малости, получаем
Таким образом, свободная энергия
| ||
|
| Поделиться: |

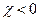 , т.е. индуцированный магнитный момент направлен против поля
, т.е. индуцированный магнитный момент направлен против поля 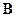 . Сегодня мы покажем, что квантование системы движущихся зарядов (электроны атомов и молекул, электроны проводимости) всегда обладают диамагнитными свойствами, которые в некоторых случаях маскируются более сильным парамагнетизмом.
. Сегодня мы покажем, что квантование системы движущихся зарядов (электроны атомов и молекул, электроны проводимости) всегда обладают диамагнитными свойствами, которые в некоторых случаях маскируются более сильным парамагнетизмом. , (1)
, (1) , связанный с соответствующим током, направлен против магнитного поля
, связанный с соответствующим током, направлен против магнитного поля 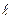 существует универсальное соотношение
существует универсальное соотношение . (2)
. (2) , (3)
, (3)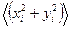 - сумма квадратов координат i-го электрона, усредненная по объему атомов, то
- сумма квадратов координат i-го электрона, усредненная по объему атомов, то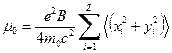 . (4)
. (4)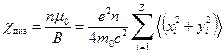 , (5)
, (5) - число атомов в 1
- число атомов в 1  .
.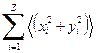 может быть вычислена квантовомеханически; по порядку величины она равна
может быть вычислена квантовомеханически; по порядку величины она равна 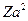 , где
, где  - линейные размеры атомов.
- линейные размеры атомов.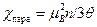 . Отношение диамагнитной восприимчивости (5) к парамагнитной по порядку величины равно
. Отношение диамагнитной восприимчивости (5) к парамагнитной по порядку величины равно , (6)
, (6)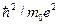 .
.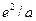 - энергия порядка атомной, то при не слишком большом атомном номере Z отношение (6) при комнатной температуре порядка
- энергия порядка атомной, то при не слишком большом атомном номере Z отношение (6) при комнатной температуре порядка 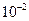 . Вот почему диамагнитные свойства проявляются только в тех веществах, атомы которых не обладают постоянным магнитным моментом.
. Вот почему диамагнитные свойства проявляются только в тех веществах, атомы которых не обладают постоянным магнитным моментом. , будет описывать в плоскости, перпендикулярной магнитному полю, круговую орбиту радиусом
, будет описывать в плоскости, перпендикулярной магнитному полю, круговую орбиту радиусом , (7)
, (7)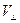 - составляющая скорости электрона в плоскости, перпендикулярной магнитному полю, а
- составляющая скорости электрона в плоскости, перпендикулярной магнитному полю, а (8)
(8)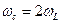 . Этому круговому движению электрона, согласно (2), соответствует магнитный момент
. Этому круговому движению электрона, согласно (2), соответствует магнитный момент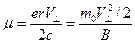 , (9)
, (9)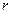 посредством равенства (7). Для электронного газа, подчиняющегося классической статистике,
посредством равенства (7). Для электронного газа, подчиняющегося классической статистике, 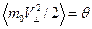 . Поэтому диамагнитная восприимчмвость
. Поэтому диамагнитная восприимчмвость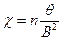 . (10)
. (10)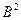 . Можно показать, что полученный нами неправильный результат связан с тем, что мы не рассматриваем поверхности (границы) тела, внутри которого движутся электроны. Вблизи поверхности электроны не могут описывать полные круговые орбиты и это приводит к появлению поверхностного тока в образце, который полностью компенсирует магнитные моменты круговых орбит электрона в твердом теле.
. Можно показать, что полученный нами неправильный результат связан с тем, что мы не рассматриваем поверхности (границы) тела, внутри которого движутся электроны. Вблизи поверхности электроны не могут описывать полные круговые орбиты и это приводит к появлению поверхностного тока в образце, который полностью компенсирует магнитные моменты круговых орбит электрона в твердом теле.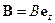 . Выберем векторный потенциал в калибровке Ландау
. Выберем векторный потенциал в калибровке Ландау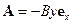 . (14)
. (14) , (15)
, (15)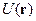 - потенциальная энергия электрона.
- потенциальная энергия электрона. , (16)
, (16)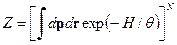 (17)
(17)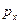 ,
,  и
и 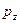 на
на ,
, 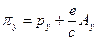 ,
,  . (18)
. (18)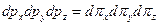 . Пределы интегрирования остаются прежними, и так как определенный интеграл от переменных интегрирования не зависит, то Z и следовательно свободная энергия F от магнитного поля B не зависят. Соответственно, в этом случае магнитная восприимчивость равна нулю.
. Пределы интегрирования остаются прежними, и так как определенный интеграл от переменных интегрирования не зависит, то Z и следовательно свободная энергия F от магнитного поля B не зависят. Соответственно, в этом случае магнитная восприимчивость равна нулю.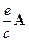 в гамильтониан электрона в магнитном поле.
в гамильтониан электрона в магнитном поле. (калибровка Ландау) в качестве полного набора квантовых чисел выступают проекция
(калибровка Ландау) в качестве полного набора квантовых чисел выступают проекция 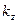 волнового вектора на направление магнитного поля (на ось z), компонента
волнового вектора на направление магнитного поля (на ось z), компонента 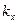 волнового вектора по оси х, номер уровня Ландау
волнового вектора по оси х, номер уровня Ландау  . Волновые функция и энергии одноэлектронного состояния
. Волновые функция и энергии одноэлектронного состояния 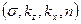 даетюся выражениями
даетюся выражениями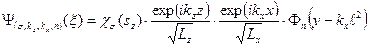 , (19)
, (19)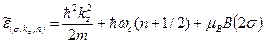 . (20)
. (20) . Ясно, что поскольку электрон находится в фиксированном макроскопически большом объеме, то допустимы только такие значения
. Ясно, что поскольку электрон находится в фиксированном макроскопически большом объеме, то допустимы только такие значения  . (21)
. (21)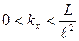 . (22)
. (22) . (23)
. (23) . По определению
. По определению . (24)
. (24) . (25)
. (25) . (26)
. (26)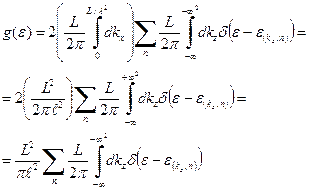 . (28)
. (28)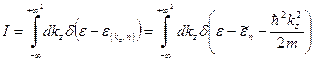 . (29)
. (29) . (30)
. (30) и затем воспользоваться основным свойством дельта-функции.
и затем воспользоваться основным свойством дельта-функции. . Также он обращается в нуль в точке
. Также он обращается в нуль в точке 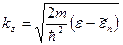 . Поэтому прежде, чем производить замену переменной, область интегрирования нужно разбить на две части так, чтобы в каждую область попадал только один нуль аргумента дельта-функции. В нашем случае, очевидно, область интегрирования удобно разбить точкой
. Поэтому прежде, чем производить замену переменной, область интегрирования нужно разбить на две части так, чтобы в каждую область попадал только один нуль аргумента дельта-функции. В нашем случае, очевидно, область интегрирования удобно разбить точкой 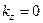 [1]
[1]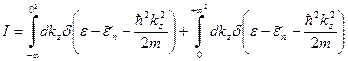 . (31)
. (31)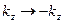
 . (32)
. (32)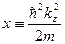 . (33)
. (33)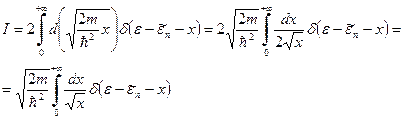
 . (34)
. (34) - тета-функция Хэвисайда.
- тета-функция Хэвисайда.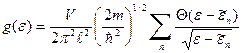 . (35)
. (35) . (36)
. (36) . (37)
. (37)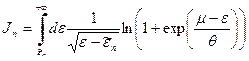 . (38)
. (38) проводим процедуру интегрирования по частям
проводим процедуру интегрирования по частям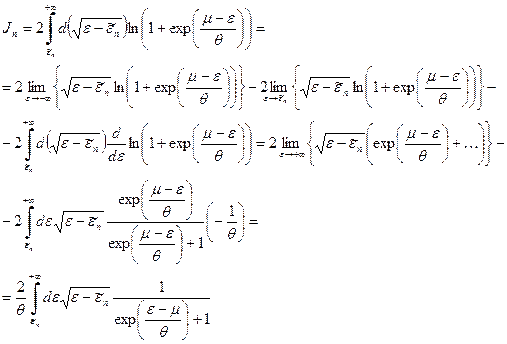 . (39)
. (39)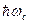 . Поэтому осуществляем обезразмеривание на энергию Ландау – делаем замену переменной
. Поэтому осуществляем обезразмеривание на энергию Ландау – делаем замену переменной 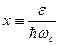 .
.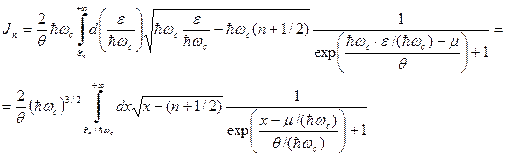 . (40)
. (40)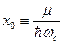 (41)
(41) . (42)
. (42) . (43)
. (43)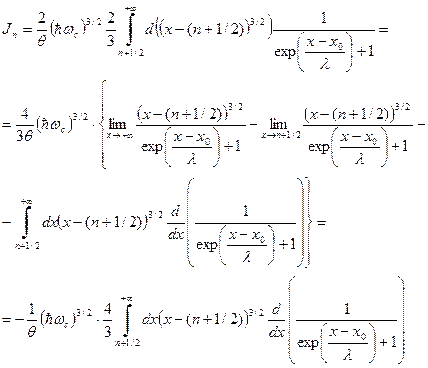 . (44)
. (44) .(45)
.(45)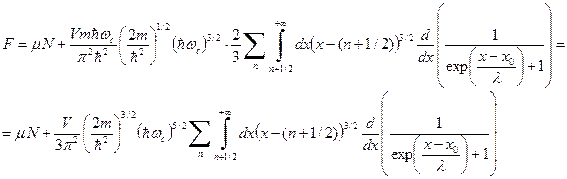 .(46)
.(46) , (47)
, (47)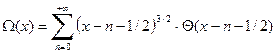 . (48)
. (48)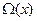 отличны от нуля только члены с
отличны от нуля только члены с 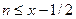 . Поэтому мы можем записать эту сумму в виде
. Поэтому мы можем записать эту сумму в виде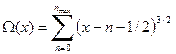 , (49)
, (49)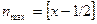 . Знак
. Знак  означает взятие целой части от числа.
означает взятие целой части от числа.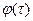 вещественного аргумента
вещественного аргумента  , то
, то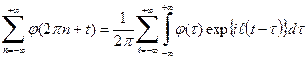 . (50)
. (50)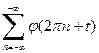 , где
, где  , (51)
, (51)
 . (52)
. (52)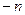 . В результате получаем
. В результате получаем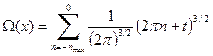 . (53)
. (53)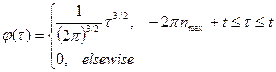 . (54)
. (54)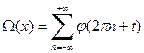 . (55)
. (55)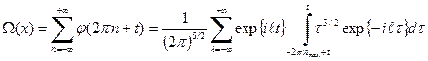 . (56)
. (56) .
.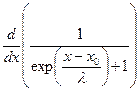 , легко убедиться, что эта функция имеет резкий максимум в точке
, легко убедиться, что эта функция имеет резкий максимум в точке  и заметно отлична от нуля только в окрестности этой точки шириной порядка
и заметно отлична от нуля только в окрестности этой точки шириной порядка  . Вне этой окрестности функция очень мала. Поэтому основной вклад в интеграл (47) дает эта окрестность. Поэтому нас интересует функция
. Вне этой окрестности функция очень мала. Поэтому основной вклад в интеграл (47) дает эта окрестность. Поэтому нас интересует функция  , т.е. когда
, т.е. когда  . В этом случае нам нужно искать функцию
. В этом случае нам нужно искать функцию 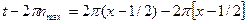 интеграла (56) можно заменить нулем. Таким образом, получаем
интеграла (56) можно заменить нулем. Таким образом, получаем . (57)
. (57) .Подставляем выражение
.Подставляем выражение  через
через 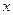 и воспользуемся тем, что
и воспользуемся тем, что  .
.
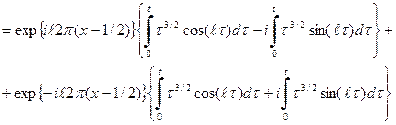 .
.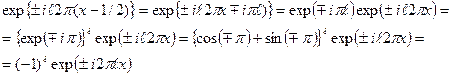 .
.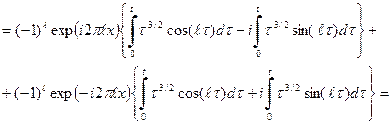
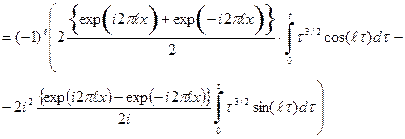 .
. и
и  , получаем
, получаем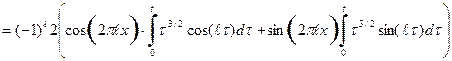 . (58)
. (58) . Проводим дважды процедуру интегрирования по частям
. Проводим дважды процедуру интегрирования по частям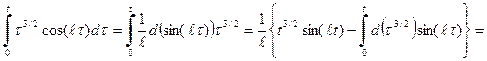


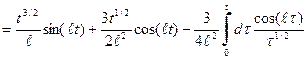 . (59)
. (59) .
. .
. , получаем
, получаем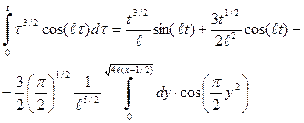 . (60)
. (60)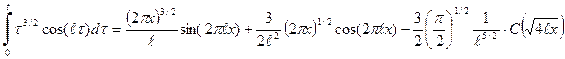 , (61)
, (61)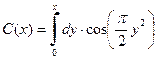 (62)
(62)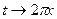 .
.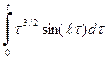 . Точно также дважды проводим процедуру интегрирования по частям.
. Точно также дважды проводим процедуру интегрирования по частям.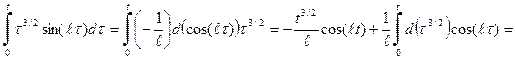

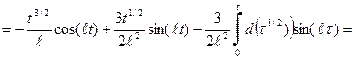
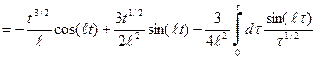 .
.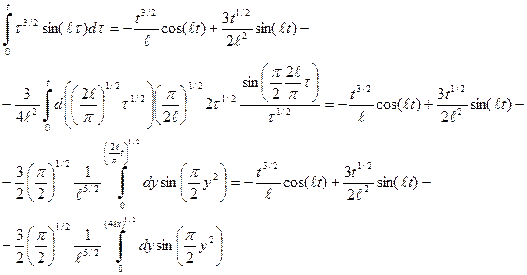
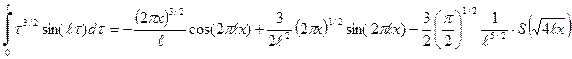 , (63)
, (63) . (64)
. (64)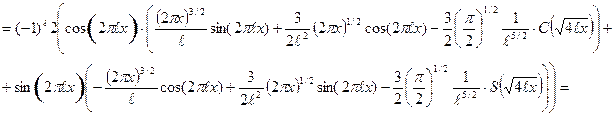 .
.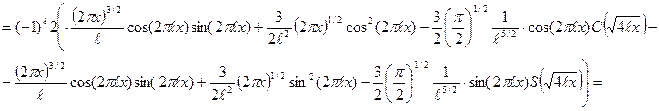

 . (65)
. (65)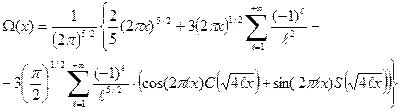 . (66)
. (66) . Для вычисления этой суммы разложим функцию
. Для вычисления этой суммы разложим функцию 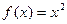 в ряд Фурье в интервале
в ряд Фурье в интервале 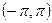 , т.е. представим эту функцию рядом
, т.е. представим эту функцию рядом , (67)
, (67)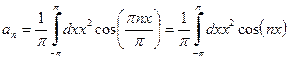 , (68)
, (68) . (69)
. (69) . Поскольку вещественная часть от мнимой экспоненты есть косинус (
. Поскольку вещественная часть от мнимой экспоненты есть косинус (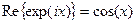 ), то мы можем написать
), то мы можем написать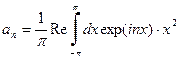 . (70)
. (70) .Проводим дважды процедуру интегрирования по частям.
.Проводим дважды процедуру интегрирования по частям.
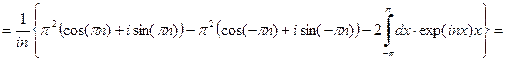
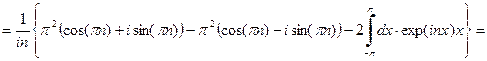

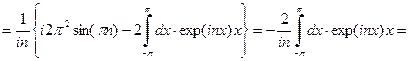
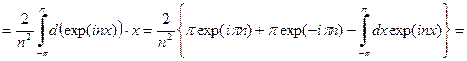
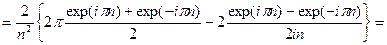
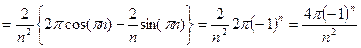 .
.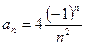 . (71)
. (71)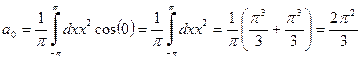
 . (72)
. (72)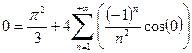 . (73)
. (73) . (74)
. (74)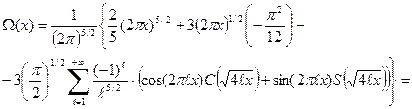

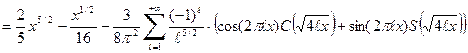 .
.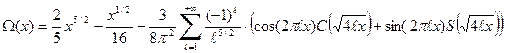 . (75)
. (75)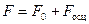 , (76)
, (76) , (77)
, (77)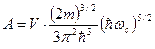 , (78)
, (78)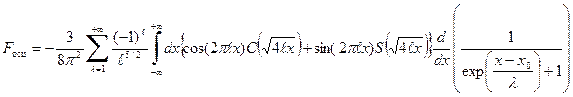 .(79)
.(79)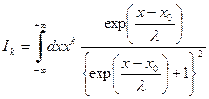 , (80)
, (80)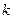 - некоторое число порядка 1. Причем нам нужно вычислять этот интеграл в случае, когда
- некоторое число порядка 1. Причем нам нужно вычислять этот интеграл в случае, когда  .
.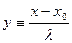 .
.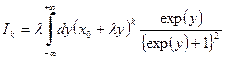 . (81)
. (81)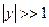 подынтегральная функция будет очень мала. Кроме того, у нас
подынтегральная функция будет очень мала. Кроме того, у нас 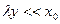 . Это дает нам возможность степенную функцию разложить в ряд Тейлора в окрестности точки
. Это дает нам возможность степенную функцию разложить в ряд Тейлора в окрестности точки  . Поскольку нас интересует первая неисчезающая поправка по магнитному полю, ограничимся в этом разложении нулевым членом, т.е., попросту говоря, заменим функцию
. Поскольку нас интересует первая неисчезающая поправка по магнитному полю, ограничимся в этом разложении нулевым членом, т.е., попросту говоря, заменим функцию 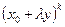 на ее значение в точке y=0.
на ее значение в точке y=0. . (82)
. (82) , получаем
, получаем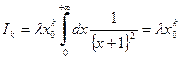 . (83)
. (83) , (84)
, (84) , (85)
, (85) . (86)
. (86)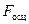 . Входящие в интеграл
. Входящие в интеграл 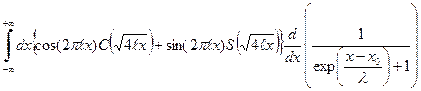 функции C и S, также как и тригонометрические функции, осциллируют с периодом ~
функции C и S, также как и тригонометрические функции, осциллируют с периодом ~  . Поэтому функция в фигурных скобках осциллируют с периодом ~
. Поэтому функция в фигурных скобках осциллируют с периодом ~ 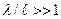 , то интеграл будет мал. Наибольшим период осцилляции будет для
, то интеграл будет мал. Наибольшим период осцилляции будет для 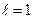 . Поэтому если
. Поэтому если 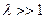 , т.е. если
, т.е. если 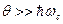 , то вклад
, то вклад 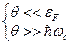 , с хорошей точностью свободная энергия нашего газа есть
, с хорошей точностью свободная энергия нашего газа есть . (87)
. (87)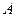 , отвечающая внешнему параметру
, отвечающая внешнему параметру 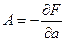 . (88)
. (88) . (89)
. (89)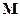 при элементарном изменении магнитного поля
при элементарном изменении магнитного поля 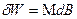 . (90)
. (90)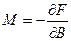 . (91)
. (91)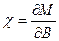 . (92)
. (92)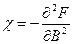 . (93)
. (93) (
(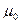 - химический потенциал в отсутствие магнитного поля). Поэтому химический потенциал нашего газа в магнитном поле мы можем разложить по этому малому параметру. Оставим в этом разложении оставим только первую неисчезающую поправку по магнитному полю. Обозначим эту поправку
- химический потенциал в отсутствие магнитного поля). Поэтому химический потенциал нашего газа в магнитном поле мы можем разложить по этому малому параметру. Оставим в этом разложении оставим только первую неисчезающую поправку по магнитному полю. Обозначим эту поправку 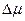 . В этом приближении химический потенциал нашего газа есть
. В этом приближении химический потенциал нашего газа есть . (94)
. (94) , либо его квадрату
, либо его квадрату 
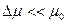 , то мы можем разложить свободную энергию по химическому потенциалу в окрестности точки
, то мы можем разложить свободную энергию по химическому потенциалу в окрестности точки 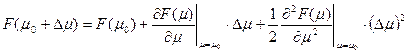 . (95)
. (95)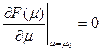 . (96)
. (96) . (97)
. (97)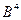 . Мы договорились оставлять в свободной энергии только первый неисчезающий член по магнитному полю. Этот первый неисчезающий член, как легко видеть, пропорционален
. Мы договорились оставлять в свободной энергии только первый неисчезающий член по магнитному полю. Этот первый неисчезающий член, как легко видеть, пропорционален  . (98)
. (98)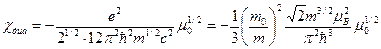 . (99)
. (99)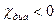 , что отвечает диамагнетизму. Таким образом, квантование Ландау приводит к диамагнетизму нашего электронного газа.
, что отвечает диамагнетизму. Таким образом, квантование Ландау приводит к диамагнетизму нашего электронного газа. ) температурным эффектом, для вырожденного газа электронов проводимости металла получаем
) температурным эффектом, для вырожденного газа электронов проводимости металла получаем . (100)
. (100) <~
<~  , в интеграле
, в интеграле 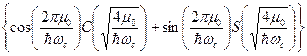 .
. . Таким образом,
. Таким образом, . (101)
. (101)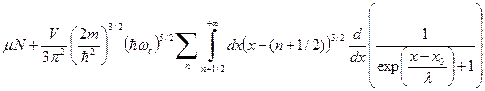
 , получим
, получим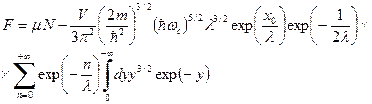 . (102)
. (102)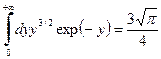 . (103)
. (103) . (104)
. (104)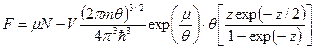 . (105)
. (105)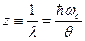 . (106)
. (106) особого интереса не представляет – в этом случае
особого интереса не представляет – в этом случае 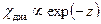 , т.е. экспоненциально мала. Поэтому мы рассмотрим другой предельный случай, когда
, т.е. экспоненциально мала. Поэтому мы рассмотрим другой предельный случай, когда  .
.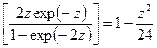 . (107)
. (107) . (108)
. (108)


