
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 6. Микроканоническое и каноническое распределения Гиббса в квантовой статистической теории.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Прежде всего, рассмотрим адиабатически изолированную систему, т.е. систему с микроканоническим распределением. Здесь имеется тонкий момент, касающийся определения адиабатически изолированной системы в квантовой статистической теории. В классической статистике под адиабатически изолированной системой мы понимали систему, для которой экранировано все взаимодействие с окружающей средой, которое не может быть с нужной точностью аппроксимировано чисто силовым постоянным во времени воздействием. В классической теории мы могли задать энергию такой системы в сколь угодно малом интервале, т.е. могли стремить неопределенность в энергии к нулю. Таким образом, в классической теории понятие замкнутой и адиабатически изолированной системы совпадают. В квантовой же механике замкнутых систем в указанном выше смысле не существует. Всякая реальная система, состоящая из атомов, всегда испытывает взаимодействие с окружающим миром, которое на практике никогда нельзя полностью экранировать. Более того, существует и другая фундаментальная (заложенная в самой природе, а не связанная с несовершенством человека) причина, не позволяющая никакой системе иметь определенное постоянное во времени значение энергии. Эта причина состоит в том, что при наблюдении системы в течение конечного момента времени
Причем эта неопределенность в принципе не может быть сделана меньше Поэтому в классической статистической теории понятие замкнутой и аддиабатически изолированной системой разнятся. Когда мы говорим о замкнутой системе, то мы заменяем всю окружающую среду внешними стационарными силовыми полями, пренебрегая вообще всем взаимодействием этой системой с окружающей средой, даже таким малым. Именно для такую абстрактную замкнутую систему, мы рассматриваем, когда определяем микросостояния нашей системы. Под адиабатически же изолированной системой в квантовой статистической теории понимается реальная система, которая не будучи строго изолированой, тем не менее столь слабо взаимодействует с внешним миром, что ее энергия изменяется в столь малом интервале
Обращаю внимание на то, что несмотря на относительную малость ширины интервала Можно показать, что число уровней в заданном конечном интервале энергетического спектра макроскопического тела возрастает с увеличением числа содержащихся в нем частиц по экспоненциальному закону, а расстояния между соседними уровнями выражаются числами Напомню, что в заданном равновесном состоянии замкнутой системы помимо интервала энергии фиксированы также число Согласно вышесказанному для замкнутой системы распределение вероятностей
Здесь Константу
Суммирование здесь ведется не по уровням энергии, а по стационарным состояниям, т.е. по различным значениям совокупности всех квантовых чисел из полного набора. Из (3) непосредственно следует, что
Введем величину
Как легко видеть, эта величина есть статистический вес - число микросостояний, возможных при заданном макросостоянии (или, как часто говорят, число микросостояний, реализующих данное макросостояние). Введем в рассмотрение псевдокронникеровскую функцию Как известно, энтропия, фигурирующая в законах термодинамики, выражается через статистический вес как
где Таким образом, энтропия
Получим теперь квантовое распределение Гиббса. Естественно, постановка задачи остается такой же как и в классической случае. Мы рассматриваем макроскопическую систему
Легко понять, что логика наших рассуждений должна быть, по сути, такой же, как и в классическом случае. Точно также мы исходим из того, что совокупность нашей системы и термостата (в принятых нами обозначениях система
Здесь энергия Как обсуждалось выше, при описании равновесного состояния системы Гамильтониан замкнутой системы «рассматриваемое тело+окружающая среда» с огромной точностью можно приблизить суммой Гамильтонианов тела и окружающей среды. Таким образом, гамильтониан системы
Тогда полный набор квантовых чисел
Тогда условие, определяющее возможные микросостояния нашей системы и термостата запишется как
и для вероятности микросостояний замкнутой системы
Нас интересует полная вероятность
Рассмотрим величину
Как легко видеть, эта величина представляет собой число микросостояний, в которых может находиться термостат при заданном микросостоянии нашей системы – число микросостояний термостата, энергия которых попадает в интервал Введем в рассмотрение величину
Как хорошо известно, логарифм при больших аргументах является очень медленно растущей функцией. Поэтому Теперь вспомним вытекающее из эксперимента свойство распределения энергии равновесной системы по ее частям. Из этого свойства непосредственно следует, что чем меньше часть равновесной системы, тем меньшая доля внутренней энергии всей системы приходится на эту часть. Поскольку наша система есть малая (но макроскопическая) часть системы
Следовательно, вероятность микросостояния нашей системы
Величина Введем независящую от микросостояния величину
Тогда вероятность (4.10) запишется в виде
Поскольку при замене энергии Как легко видеть, нормировочный множитель дается выражением
Нормировочный множитель
и попытаться через эту величину выразить внутренние параметры нашей системы – ее внутреннюю энергию, обобщенные силы и энтропию. Дифференцируя (4.14) по внешнему параметру
Таким образом, мы получаем, что термодинамические обобщенные силы выражаются через функцию состояния (21) как
Дифференцируя (4.14) по температуре
Таким образом, внутренняя энергия выражается через функцию состояния
Перейдем теперь к вычислению энтропии нашей системы. Для этого воспользуемся тем обстоятельством, что с подавляющей вероятностью реализуются микросостояния нашей системе с энергиями, лежащими в малой окрестности внутренней энергии
Следовательно,
С учетом (25), находим
Таким образом, мы видим, что функция состояния Рассмотрим теперь распределение Гиббса с переменным числом частиц (большое каноническое распределение) В этом случае мы должны рассматривать явную зависимость модельного Гамильтониана системы Соответственно, условия, определяющие микросостояния нашей системы и термостата, примут вид
Здесь Полная вероятность микросостояния нашей системы (вероятность того, что в нашей системе
Здесь
Поскольку число частиц в нашей системе и число частиц в термостате связанны друг с другом соотношением Аналогично, предыдущей задачи вероятность микросостояния нашей системы мы можем представить в виде
где
Поскольку наша система есть малая часть системы Поэтому также как и в предыдущей задаче, функцию
Соответственно, вероятность микросостояния нашей системы принимает вид
Здесь независящую от микросостояния величину
и
На основании принципа соответствия мы можем утверждать, что Теперь, следуя общей логике, определим через нормировочный множитель функцию состояния системы
и, дифференцируя эту функцию по внешним параметрам, температуре и химическому потенциалу, попытаемся выразить через нее внутренние термодинамические характеристики нашей системы – внутреннюю энергию, термодинамические обобщенные силы, среднее число частиц в системе и ее энтропию. Дифференцируя (38) по химическому потенциалу
Из условия нормировки
Подставляя в (5.11), находим
Таким образом, среднее число частиц выражается через функцию состояния
Дифференцируя (38) по внешнему параметру
Дифференцируя (38) по температуре, получим выражение для внутренней энергии
Рассуждая также как и в предыдущей задаче, получим для энтропии
Таким образом, мы видим, что функция состояния
|
||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 534; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.58.83 (0.013 с.) |

 всегда возникает неопределенность в энергии
всегда возникает неопределенность в энергии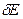 ~
~  . (1)
. (1) (
(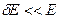 ), что можно считать равновероятным реализацию любого ее микросостояния с энергией, попадающей в этот интервал. Другими словами, замкнутая система – система, для которой справедлив принцип равной вероятности.
), что можно считать равновероятным реализацию любого ее микросостояния с энергией, попадающей в этот интервал. Другими словами, замкнутая система – система, для которой справедлив принцип равной вероятности. (где
(где  - величина порядка числа частиц в теле), безразлично в каких единицах, т.к. разница между различными единицами энергии совершенно не существенна для такого чудовищно малого числа. Такой спектр называется квазинепрерывным.
- величина порядка числа частиц в теле), безразлично в каких единицах, т.к. разница между различными единицами энергии совершенно не существенна для такого чудовищно малого числа. Такой спектр называется квазинепрерывным. (ограничен изолирующими стенками), а также остальные внешние параметры
(ограничен изолирующими стенками), а также остальные внешние параметры  , задающие проникающие сквозь изолирующие стенки внешние стационарные силовые поля.
, задающие проникающие сквозь изолирующие стенки внешние стационарные силовые поля. различных микросостояний есть
различных микросостояний есть . (2)
. (2) - энергия микросостояния
- энергия микросостояния  .
. легко найти из условия нормировки
легко найти из условия нормировки . (3)
. (3) . (4)
. (4) . (5)
. (5) , (6)
, (6)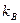 - постоянная Больцмана. Можно показать, что энтропия с очень большой точностью не зависит от величины
- постоянная Больцмана. Можно показать, что энтропия с очень большой точностью не зависит от величины  . (7)
. (7) , которая находится в равновесии с очень большим по сравнению с ней термостатом
, которая находится в равновесии с очень большим по сравнению с ней термостатом  . Мы считаем, что при взаимодействии системы с термостатом число частиц в системе не изменяется.
. Мы считаем, что при взаимодействии системы с термостатом число частиц в системе не изменяется. ) является изолированной. Поэтому вероятность ее микросостояний
) является изолированной. Поэтому вероятность ее микросостояний . (8)
. (8) задает состояние равновесия всей замкнутой системы
задает состояние равновесия всей замкнутой системы 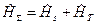 . (9)
. (9) для микросостояний системы
для микросостояний системы  нашей системы и полного набора квантовых чисел термостата
нашей системы и полного набора квантовых чисел термостата  . Уровни энергии
. Уровни энергии 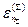 системы
системы 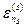 нашей системы и уровней энергии
нашей системы и уровней энергии 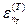 термостата
термостата . (10)
. (10) , (11)
, (11) . (12)
. (12) микросостояния
микросостояния  . (13)
. (13) . (14)
. (14) . Прежде всего, заметим, что поскольку спектр нашей системы квазинепрерывный, то аргумент функции
. Прежде всего, заметим, что поскольку спектр нашей системы квазинепрерывный, то аргумент функции  меняется практически непрерывно. Кроме того, в силу квазинепрерывности спектра термостата
меняется практически непрерывно. Кроме того, в силу квазинепрерывности спектра термостата  . (15)
. (15) очень сильно сгладит особенности функции
очень сильно сгладит особенности функции  может быть с огромной точностью аппроксимирована гладкой функцией, очень хорошей с математической точки зрения. В частности, эту функцию можно раскладывать в ряд.
может быть с огромной точностью аппроксимирована гладкой функцией, очень хорошей с математической точки зрения. В частности, эту функцию можно раскладывать в ряд. , и с большой точностью функцию
, и с большой точностью функцию  , ограничившись только первой степенью
, ограничившись только первой степенью 
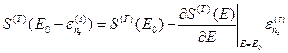 . (16)
. (16) . (17)
. (17) не зависит от микросостояния нашей системы и может быть включена в нормировочный множитель, который мы обозначим
не зависит от микросостояния нашей системы и может быть включена в нормировочный множитель, который мы обозначим  .
. . (18)
. (18) . (19)
. (19) на классическую функцию Гамильтона нашей системы, выражение (4.12) должно переходить в классическое распределение Гиббса, то мы можем утверждать, что величина
на классическую функцию Гамильтона нашей системы, выражение (4.12) должно переходить в классическое распределение Гиббса, то мы можем утверждать, что величина  есть термодинамическая температура, измеренная в энергетических единицах.
есть термодинамическая температура, измеренная в энергетических единицах. . (20)
. (20) называется статистической суммой. Как легко понять, статистическая сумма есть квантовый аналог статистического интеграла (при переходе в классическую механику, статистическая сумма, очевидно, перейдет в статистический интеграл). Поэтому здесь логично ввести в рассмотрение функцию состояния
называется статистической суммой. Как легко понять, статистическая сумма есть квантовый аналог статистического интеграла (при переходе в классическую механику, статистическая сумма, очевидно, перейдет в статистический интеграл). Поэтому здесь логично ввести в рассмотрение функцию состояния , (21)
, (21) , находим
, находим , (22)
, (22) . (23)
. (23) . (24)
. (24) как
как . (25)
. (25) . Ширина этой окрестности определяется относительной флуктуацией, которая, как мы знаем очень мала. Величины, фигурирующие в термодинамике, не зависят от этих флуктуаций. Поэтому с точки зрения термодинамики наша система полностью эквивалентна замкнутой системе с энергией
. Ширина этой окрестности определяется относительной флуктуацией, которая, как мы знаем очень мала. Величины, фигурирующие в термодинамике, не зависят от этих флуктуаций. Поэтому с точки зрения термодинамики наша система полностью эквивалентна замкнутой системе с энергией  . (26)
. (26) . (27)
. (27)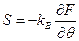 . (28)
. (28) от числа частиц
от числа частиц  в ней. Поэтому когда мы задаем микросостояние нашей системы, мы сначала должны указать число частиц в ней, а затем указать базисный собственный вектор
в ней. Поэтому когда мы задаем микросостояние нашей системы, мы сначала должны указать число частиц в ней, а затем указать базисный собственный вектор  гамильтониана
гамильтониана 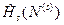 нашей системы, когда в ней имеется это число частиц. Аналогично, будет задаваться и состояние термостата.
нашей системы, когда в ней имеется это число частиц. Аналогично, будет задаваться и состояние термостата. . (29)
. (29) - число частиц в изолированной системе
- число частиц в изолированной системе  . (30)
. (30) (31)
(31) , то фиксировав число частиц в нашей системе, мы тем самым фиксируем и число частиц в термостате. Поэтому в формуле (30) суммирование осуществляется по квантовым состояниям термостата в случае, когда он содержит заданное число частиц
, то фиксировав число частиц в нашей системе, мы тем самым фиксируем и число частиц в термостате. Поэтому в формуле (30) суммирование осуществляется по квантовым состояниям термостата в случае, когда он содержит заданное число частиц  .
. , (32)
, (32)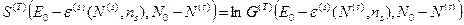 , (33)
, (33) - число микросостояний, в которых может находиться термостат при условии, что наша система находится в микросостоянии
- число микросостояний, в которых может находиться термостат при условии, что наша система находится в микросостоянии  .
. и энергией
и энергией  .
. мы можем разложить в ряд Тейлора, ограничившись только первой степенью
мы можем разложить в ряд Тейлора, ограничившись только первой степенью 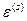
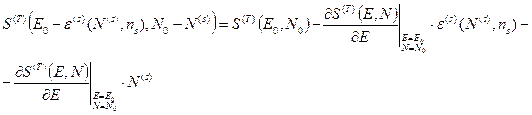 .(34)
.(34) (35)
(35)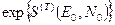 мы включили в нормировочный множитель
мы включили в нормировочный множитель  , и также ввели независящие от микросостояния величины
, и также ввели независящие от микросостояния величины (36)
(36) (37)
(37) - химический потенциал.
- химический потенциал.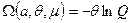 , (38)
, (38) , (39)
, (39) , находим нормировочный множитель
, находим нормировочный множитель 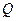 (он называется большой статистической суммой)
(он называется большой статистической суммой) (40)
(40) , (41)
, (41) как
как . (42)
. (42) . (43)
. (43) . (44)
. (44) . (45)
. (45) представляет собой термодинамический потенциал нашей системы- так называемый большой термодинамический потенциал.
представляет собой термодинамический потенциал нашей системы- так называемый большой термодинамический потенциал.


