
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 3. Микроканоническое и каноническое распределения Гиббса в классической статистической теорииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Изолированная система. Микроканоническое распределение
Рассмотрим ситуацию, когда изучаемая система является адиабатически изолированной от окружающей среды или, иначе, замкнутой. В этом случае изучаемая система отделена от окружающей среды адиабатическими стенками, которые препятствуют как обмену частицами, так и теплообмену между системой и окружающей средой. При этом принципиально, что стенки препятствуют именно взаимодействию. Эта постановка задачи вовсе не исключает наличие влияния окружающей среды, которое может быть с большой степенью точности аппроксимировано чисто силовым внешним воздействием. Другими словами, под замкнутой мы понимаем систему, все существенное влияние на которую можно с достаточной точностью учесть, рассмотрев ее во внешних стационарных силовых полях. Главное, что замкнутая система не обменивается с окружающей средой ни частицами, ни энергией. При таком задании нашей системы мы фиксируем число частиц в ней Задача о функции распределения изолированной системы является исходной для статистической теории. Вид функции распределения для замкнутой системы являются отправной точкой при нахождении канонического и большого канонического распределения. Вид функции распределения для адиабатически изолированной системы непосредственно вытекает из постулата, который носит название принципа равной вероятности. Этот принцип состоит в следующем. Состояние равновесия нашей замкнутой системы задается ее энергией Е. Функция Гамильтона системы есть ни что иное, как ее полная энергия. Следовательно, микросостояния нашей системы, возможные в заданном состоянии равновесия, определяются условием
Никакие другие микросостояния нашей системы в этом ее состоянии равновесия не возможны. Утверждение постулата равной вероятности состоит в том, что с равной вероятностью реализуется любое микросостояние, возможное в данном состоянии равновесия изолированной системы. Непосредственно из постулата равной вероятности следует, что функция распределения нашей замкнутой системы имеет вид
Действительно, пусть энергия нашей системе является не строго постоянной, а может меняться в очень малом интервале от
Пусть ширина интервала энергии
где С – константа. Равновесное значение макроскопического параметра, как мы значем, есть
Теперь для того, чтобы перейти от квазизамкнутой системы к истинно замкнутой, мы должны устремить
Таким образом, функцию распределения адиабатически изолированной системы мы можем написать как произведение нормировочной постоянной на дельта-функцию Дирака, аргумент которой есть разность функции Гамильтона нашей системы и энергии E
Значение постоянной
Подставляем в условие нормировки явный вид функции распределения и переходим от интегрирования по фазовому пространству к интерированию по энергии в соответствии с той теоремой, которую сформулированной на прошлой лекции. В результате получим
где
объем фазового пространства, ограниченный поверхностью постоянной энергии Воспользовавшись основным свойством дельта-функции
В результате получаем
Отсюда постоянная
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 922; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |


 , ее объем
, ее объем  и остальные внешние параметры
и остальные внешние параметры  , а также ее энергию. Причем речь идет не о внутренней энергии, а именно об энергии в обычном механическом понимании. Состояние равновесия такой системы задается внешними параметрами и ее энергией. Для полноты информации – для того, чтобы написать функцию Гамильтона нашей системы - нам еще, конечно же, нужно знать число частиц N в нашей системе. Распределение вероятности различных микросостояний замкнутой системы называется микроканоническим.
, а также ее энергию. Причем речь идет не о внутренней энергии, а именно об энергии в обычном механическом понимании. Состояние равновесия такой системы задается внешними параметрами и ее энергией. Для полноты информации – для того, чтобы написать функцию Гамильтона нашей системы - нам еще, конечно же, нужно знать число частиц N в нашей системе. Распределение вероятности различных микросостояний замкнутой системы называется микроканоническим. . (1)
. (1) . (2)
. (2) до
до  . Тогда возможные микросостояния нашей системы определяются условием
. Тогда возможные микросостояния нашей системы определяются условием . (3)
. (3) хоть и конечна, но настолько мала, что для нашей системы с большой точностью справедлив принцип равной вероятности. Т.е. ширина интервала настолько мала, что каждое микросостояние, энергия которого попадает в данный интервал, реализуется с равной вероятностью. Другими словами, функция распределения нашей системы имеет вид
хоть и конечна, но настолько мала, что для нашей системы с большой точностью справедлив принцип равной вероятности. Т.е. ширина интервала настолько мала, что каждое микросостояние, энергия которого попадает в данный интервал, реализуется с равной вероятностью. Другими словами, функция распределения нашей системы имеет вид , (4)
, (4)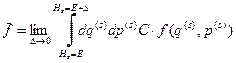 . (5)
. (5) . (6)
. (6) .
. определяется условием нормировки
определяется условием нормировки . (7)
. (7) , (8)
, (8) , (9
, (9 (10)
(10) .
. . (11)
. (11) . (12)
. (12) . (13)
. (13)


