
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 1. Статистическое описание с позиции классической механики. Функция распределения. Статистическое усреднение. Флуктуации аддитивных величин.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Лекция 2. Зависимость функции распределения от макроскопического состояния Таким образом, мы получаем
Число Введем величину
Эта величина также не зависит от микросостояния нашей системы, а определяется макроскопическим состоянием всей замкнутой системы, т.е. главным образом термостатом, поскольку по сравнению с нашей системой он просто огромен. Эта величина Итак, мы приходим к следующему выражению для функции распределения нашей системы
Постоянная
Часто эту постоянную называют статистическим интегралом данного состояния равновесия нашей системы. Подставляя в условие нормировки явный вид функции распределения, получаем, что статистический интеграл
Как не сложно видеть из этого выражения, значение статистического интеграла однозначным образом определяется внешними параметрами нашей системы и модулем канонического распределения. Таким образом, если мы знаем внешние (силовые) параметры и модуль канонического распределения, то этой информации достаточно для того, чтобы написать функцию распределения и, соответственно, вычислить все ее внутренние термодинамические параметры. Модель Изинга.
Как мы уже много раз обсуждали, главный принцип, на котором покоится физика больших ансамблей частиц, а таковым является любой объект, для которого можно ввести понятие "фаза", а соответственно и "фазовый переход", - это принцип максимальной вероятности: в природе реализуется только наиболее вероятное состояние ансамбля. Состояние ансамбля для простоты будем характеризовать только энергией E каждой возможной конфигураций частиц ансамбля и числом конфигурации с этой энергией
Свободная энергия Гиббса Чтобы определить, какое же состояние реализуется, нужно найти максимум
Заметим, что при модельном, то есть микроскопическом, подходе к описанию фазовых переходов начинают с того, что определяют подсистему всей "большой" системы, сильно изменяющуюся при фазовом переходе. В простейшем случае это какая-нибудь степень свободы, характеризующая структурную единицу вещества, например механические (или магнитные) моменты атомов в диэлектрике. Остальные "обобщенные координаты" кристалла считаются при фазовом переходе почти не изменяющимися, точнее, считается, что их изменением в процессе фазового перехода можно в первом приближении пренебречь. Так, при описании магнитных фазовых переходов, определяемых наличием в веществе ионов Рассмотрим, пожалуй, самую простую и популярную модель фазовых переходов - модель Изинга. Это модель кристалла с атомами, зафиксированными в неподвижных узлах кристаллической решетки. Каждому атому приписываются несколько возможных дискретных состояний (степеней свободы). В оригинальной модели Изинга-Ленца возможных состояний атома два. При физической интерпретации этой модели можно представить себе, что эти два состояния соответствуют заполнению узла решетки атомом А или В в упорядочивающемся бинарном сплаве состава Согласно приведенному выше принципу статистической термодинамики, функция F для модели должна быть минимальна в термодинамически стабильном равновесном состоянии. Подсчитаем свободную энергию для модели Изинга-Ленца как функцию температуры. В модели Изинга-Ленца учитываются только двухчастичные изотропные взаимодействия ближайших соседей. В этом предположении средняя энергия подсистемы моментов во внешнем поле
где V - энергия взаимодействия соседних атомов,
В этих приближениях состояния всех атомов независимы и можно подсчитать число способов реализации конфигурации с заданной энергией и величиной Вероятность реализации конфигурации "момент вверх" или "момент вниз" на одном атоме в принятом приближении среднего поля никак не влияет на его реализацию на другом атоме. По известным свойствам вероятностей независимых событий вероятность определенной конфигурации ансамбля таких моментов равна произведению вероятностей того или иного состояния атома, а по свойствам логарифмов - логарифм произведения равен сумме логарифмов, окончательно получаем
где
Качественное исследование решений этого уравнения легко провести по рис. 1. При высоких температурах
Рис.1.
Теперь уместно сделать одно замечание. В модели Изинга-Ленца учитывается только парное изотропное взаимодействие. Это приводит к тому, что самосогласованное поле фактически пропорционально среднему значению магнитного момента или параметру порядка для ферромагнитного состояния. Поэтому формально можно было бы записывать уравнения состояния относительно величины средней намагниченности Приближенный расчет F по Горскому-Бреггу-Вильямсу при вычислении внутренней энергии
По формуле Стирлинга при
Таким образом,
Как видим, уравнение состояния для определения
Однако, помня, что Решения уравнения (6) или (8), будучи подставлены в (5) или (7), дадут одни и те же равновесные значения
Лекция 1. Статистическое описание с позиции классической механики. Функция распределения. Статистическое усреднение. Флуктуации аддитивных величин. Составляя уравнения движения механической системы и интегрируя их, мы принципиально можем получить исчерпывающие сведения об эволюции механической системы. Однако когда мы попытаемся применить методы механики к макроскопической системе, т.е. системе с колоссальным порядка числа Авогадро числом степеней свободы, мы столкнемся с необходимостью составить и решить столь же гигантское число дифференциальных уравнений, что представляется, вообще говоря, невозможным на практике. Следует отметить, что даже если мы получим общее решение уравнений движения такой системы, то совершенно невозможно будет подставить в это решение начальные условия. Таким образом, нет никакой возможности дать полное механическое описание эволюции состояния макроскопической системы, даже в том случае, когда она замкнута. Однако, к счастью, для описания подавляющего числа явлений, связанных с макрообъектами, достаточно знать только макроскопические величины, т.е. величины, характеризующие не отдельные частицы, а все тело или его отдельные макроскопические части. Такие величины обладают весьма замечательным свойством. Из опыта известно, что если макроскопическое тело поместить в стационарные условия, то по истечении некоторого времени (времени релаксации) оно придет в состояние термодинамического равновесия. Это состояние характеризуется тем, что все макроскопические величины подавляющую часть времени являются практически постоянными и лишь сравнительно очень редко испытывают сколько-нибудь заметные отклонения. Причем данное обстоятельство тем более справедливо, чем сложнее и больше рассматриваемое тело. Указанный характер поведения макроскопических величин позволяет при описании таких систем вместо истинной зависимости этих величин от времени использовать их средние по времени значения. Для величины
Статистическая физика представляет собой математический аппарат, который позволяет вычислять эти средние, не прибегая при этом к указанной формуле. Легко понять что, с помощью этой формулы совершенно нельзя сделать никакие теоретические предсказания значений термодинамических характеристик. Для того, чтобы вычислить среднее с помощью этой формулы, нужно вначале определить зависимость от времени механического состояния системы, т.е. зависимость от времени всех обобщенных координат и скоростей, что невозможно на практике из-за колоссального числа степеней свободы. К счастью оказывается, что как раз наличие у макроскопической системы колоссального числа степеней свободы позволяет вычислять такие средние, не прибегая к этому непосредственному определению. Прежде, чем перейти непосредственно к обсуждению способов вычисления этих средних, договоримся о некоторой терминологии. Прежде всего, механическое состоянии системы будем называть ее микросостоянием. Далее введем понятие фазового пространства механической системы. Каждое микросостояние системы с Приступим теперь к рассмотрению вопроса о том, как можно вычислять статистические средние макроскопических величин, не решая при этом полную механическую задачу Прежде всего заметим, что макроскопические тела, с которыми нам приходится иметь дело, являются относительно малыми частями большой замкнутой системы, состоящей из внешних тел вместе со средой, в которую они погружены. Например, в случае макроскопического тела, помещенного в термостат, это тело вместе с термостатом образует замкнутую систему. При этом изучаемая нами система очень мала по сравнению с термостатом, так что влияние нашей системы на термодинамическое состояние термостата пренебрежимо мало. Поэтому постановка нашей задачи должна быть следующей. Рассмотрим замкнутую макроскопическую систему, т.е. систему, не взаимодействующую ни с какими другими телами. Выделим в этой системе некоторую ее часть, которая с одной стороны весьма мала по сравнению со всей системой, а с другой стороны также является макроскопической. Такие относительно малые, но при этом макроскопические части мы будем называть подсистемами. Наша цель состоит в том, чтобы научиться вычислять средние по времени значения макроскопических величин для этих подсистем, не прибегая к решению полной механической задачи. Подсистема сама является макроскопической системой, но при этом уже отнюдь не замкнутой. Напротив, она испытывает всевозможные воздействия со стороны остальных частей системы. Из-за наличия у этих остальных частей системы большого числа степеней свободы эти взаимодействия будут иметь весьма сложный и запутанный характер. Поэтому микросостояние подсистемы будет меняться со временем весьма сложным и запутанным образом. Как раз этот сложный и запутанный характер эволюции микросостояния подсистемы и позволяет подойти к решению поставленной задачи с другой стороны. В основе этого подхода лежит то обстоятельство, что благодаря сложному и запутанному характеру эволюции микросостояния нашей подсистемы, она за достаточно большой промежуток времени успеет побывать достаточно большое число раз во всех возможных своих микросостояниях. Точнее это обстоятельство можно сформулировать следующим образом. Выделим достаточно малый объем фазового пространства
Этот предел можно, очевидно, рассматривать как вероятность того, что при наблюдении нашей подсистемы в некоторый произвольный момент времени мы обнаружим ее находящейся в данном участке Переходя к бесконечно малым элементам фазового пространства, мы можем определить вероятность
Функция Функция распределения, очевидно должна удовлетворять условию нормировки
где интеграл берется по всему фазовому пространству подсистемы. Условие нормировки есть просто отражение того простого факта, что вероятность того, что подсистема в любой момент времени обязательно находится в каком-то своем микросостоянии. Вычисление этой функции распределения как раз и является основной задачей статистической теории. Оказывается, что функцию распределения можно найти, не решая полную механическую задачу. Зная функцию распределения, мы сразу можем вычислить вероятности различных значений любой физической величины
где интегрирование ведется по всему фазовому пространству данной подсистемы. В силу своего определения вероятности, с помощью формулы (3), усреднение с помощью функции распределения, или как говорят, статистическое усреднение полностью эквивалентно усреднению по времени (1). Однако статистическое усреднение обладает тем преимуществом, что оно освобождает нас от необходимости следить за изменением истинного значения физической величины Следует отметить, что статистическая теория не дает такой исчерпывающе полной и однозначной информации о системе, какую дают методы классической механики. Выводы и предсказания статистической теории в отличие от результатов классической механики имеют вероятностный характер. Причем вероятностный характер результатов статистической теории сам по себе отнюдь не лежит в самой природе рассматриваемых ею объектов, он есть лишь следствие того, что эти результаты получаются на основании гораздо меньшего количества данных, чем это нужно было бы для полного механического описания (не требуются начальные значения всех координат и импульсов). Тем не менее, при практическом применении статистической теории к макроскопическим телам в состоянии термодинамического равновесия ее вероятностный характер обычно совершенно не проявляется. Дело в том, что, как уже обсуждалось, если наблюдать любое макроскопическое тело, находящееся в состоянии термодинамического равновесия, в течение достаточно большого промежутка времени, то окажется, что все характеризующие тело макроскопические величины являются практически постоянными и лишь сравнительно очень редко испытывают сколько-нибудь заметные отклонения. В терминах статистического распределения это означает, что если с помощью функции распределения
Рис.1.
Таким образом, давая возможность вычислять средние значения величин, характеризующих макроскопические тела, статистическая теория тем самым позволяет делать предсказания, оправдывающиеся с весьма большой точностью для подавляющей части времени наблюдения. В этом смысле предсказания статистики приобретают практически определенный, а не вероятностный характер. Далее, обратим внимание на тот факт, что энергия взаимодействия макроскопической системы со своим окружением существенно меньше ее внутренней энергии. В самом деле, во взаимодействии подсистемы с окружающими частями большой системы в основном принимают участие частицы, находящиеся вблизи ее поверхности. Относительное число частиц вблизи поверхности по сравнению с полным числом частиц в подсистеме быстро уменьшается с ростом размеров системы, и при достаточной большой величине подсистемы энергия ее взаимодействия со своим окружением будет существенно меньше внутренней энергии подсистемы. Такое соотношение между энергией взаимодействия подсистем и их внутренней энергией, во-первых, служит обоснованием того, что функция распределения данной подсистемы зависит только от ее координат и импульсов, и не зависит от микросостояния ее окружения. Кроме того, указанное обстоятельство дает возможность считать подсистемы независимыми в статистическом смысле. Остановимся здесь более подробно. Рассмотрим каких-либо две подсистемы. Первую подсистему обозначим цифрой 1, втору цифрой – 2. Будем обозначим обобщенные координаты и импульсы первой подсистемы
Из написанного равенства непосредственно следует, что
т.е. функция распределения составной подсистемы “1+2” равна произведению функций распределения подсистемы 1 и подсистемы 2. Аналогичное соотношение можно написать и для совокупности нескольких подсистем, при условии, конечно, что совокупность всех этих подсистем все еще составляет малую часть замкнутой системы.
Рис.2
Можно, очевидно, утверждать и обратное, если распределение вероятностей сложной системы распадается на произведение множителей, каждый из которых зависит только от микросостояния одной из ее, то это значит, что эти части статистически независимы, причем каждый из множителей пропорционален вероятности состояний соответствующих подсистем. Теперь рассмотрим какую-либо величину
Подставляем явный вид нашей разности Отсюда
Оставшийся интеграл равен единице в силу условия нормировки функции распределения. Таким образом, получаем, что среднее нашей разности
всегда равно нулю, не зависимо от того, как ведет себя наша величина В свете сказанного понятно, что в качестве искомой характеристики удобно брать среднее значение квадрата этой разности
Квадрат разности Теперь получим одно полезное выражение для средней квадратичной флуктуации. Для этого в определении этой величины давайте раскроем квадрат разности. В результате получим
Далее воспользуемся тем, что среднее суммы равно сумме средних. Таким образом, имеем
Теперь воспользуемся тем, что константу можно выносить за знак усреднения. Вынося в третьем слагаемом константу
Сокращая одинаковые слагаемые, окончательно имеем
Таким образом, среднеквадратичная флуктуация определяется разностью среднего квадрата и квадрата среднего. Отношение |
|
| Поделиться: |

 . (25)
. (25) определяется условием нормировки.
определяется условием нормировки. . (26)
. (26) называется модулем канонического распределения.
называется модулем канонического распределения.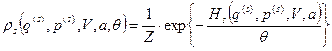 . (27)
. (27) . (28)
. (28) . (29)
. (29) . Согласно теореме Гиббса вероятность реализации состояния ансамбля
. Согласно теореме Гиббса вероятность реализации состояния ансамбля . (3)
. (3) пропорциональна
пропорциональна  На этом соотношении покоится вся статистическая термодинамика.
На этом соотношении покоится вся статистическая термодинамика. , где
, где  зависит от набора внутренних обобщенных координат ансамбля: положений атомов, ориентации их моментов; структуры, энергии коллективных возбуждений в ансамбле и т.д. Этот же результат можно получить, находя минимум физически более интересной, четко определенной в термодинамике величины свободной энергии Гельмгольца:
зависит от набора внутренних обобщенных координат ансамбля: положений атомов, ориентации их моментов; структуры, энергии коллективных возбуждений в ансамбле и т.д. Этот же результат можно получить, находя минимум физически более интересной, четко определенной в термодинамике величины свободной энергии Гельмгольца: . (4)
. (4) или
или  , часто можно в первом приближении считать атомы зафиксированными на своих местах в кристаллической решетке (то есть пренебречь магнитострикцией).
, часто можно в первом приближении считать атомы зафиксированными на своих местах в кристаллической решетке (то есть пренебречь магнитострикцией). . Первоначальная интерпретация предполагала, что эти два состояния атома соответствуют магнитному моменту, который может иметь только два направления вверх и вниз на плоской квадратной решетке. Нас будет интересовать не физическая интерпретация модели, а то, что модель Изинга позволяет прояснить, как вообще возникает фазовый переход второго рода. Ниже, только для облегчения восприятия, будем описывать модель в терминах упорядочивающихся магнитных моментов атомов ферромагнетика.
. Первоначальная интерпретация предполагала, что эти два состояния атома соответствуют магнитному моменту, который может иметь только два направления вверх и вниз на плоской квадратной решетке. Нас будет интересовать не физическая интерпретация модели, а то, что модель Изинга позволяет прояснить, как вообще возникает фазовый переход второго рода. Ниже, только для облегчения восприятия, будем описывать модель в терминах упорядочивающихся магнитных моментов атомов ферромагнетика.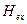 может быть записана в виде
может быть записана в виде , (5)
, (5) , если i и j - ближайшие соседи и
, если i и j - ближайшие соседи и  = 0 во всех остальных случаях; угловыми скобками обозначают среднее значение величины по подсистеме. Часто принимаемое приближение при расчетах моделей (приближение хаотических фаз) заключается в том, что полагают
= 0 во всех остальных случаях; угловыми скобками обозначают среднее значение величины по подсистеме. Часто принимаемое приближение при расчетах моделей (приближение хаотических фаз) заключается в том, что полагают  . Для наших целей этого приближения тоже достаточно, хотя при этом исключаются многие интересные эффекты влияния ближнего порядка на переходы. Предположим кроме этого, что упорядочение моментов будет "ферромагнитным", то есть после упорядочения все они будут направлены в одну сторону. Обозначим
. Для наших целей этого приближения тоже достаточно, хотя при этом исключаются многие интересные эффекты влияния ближнего порядка на переходы. Предположим кроме этого, что упорядочение моментов будет "ферромагнитным", то есть после упорядочения все они будут направлены в одну сторону. Обозначим  , назовем эту величину параметром порядка и определим эффективное поле, действующее на каждый атом со стороны окружающих
, назовем эту величину параметром порядка и определим эффективное поле, действующее на каждый атом со стороны окружающих . (6)\
. (6)\ (способ расчета по Бреггу-Вильямсу). Однако более наглядно принять, что конфигурация определяется энергией и эффективным полем, действующим на каждый атом (приближение самосогласованного поля Вейса). Тогда вероятность реализации состояния "момент равен +1" на одном атоме, согласно соотношению Гиббса, равна
(способ расчета по Бреггу-Вильямсу). Однако более наглядно принять, что конфигурация определяется энергией и эффективным полем, действующим на каждый атом (приближение самосогласованного поля Вейса). Тогда вероятность реализации состояния "момент равен +1" на одном атоме, согласно соотношению Гиббса, равна  , а состояния "момент равен - 1":
, а состояния "момент равен - 1":  . Величина
. Величина  называется самосогласованным полем Вейса.
называется самосогласованным полем Вейса. , (7)
, (7) . Уравнение (7) дает выражение для избыточной (неравновесной) свободной энергии в приближении самосогласованного поля Вейса. Самосогласованным поле
. Уравнение (7) дает выражение для избыточной (неравновесной) свободной энергии в приближении самосогласованного поля Вейса. Самосогласованным поле  называется потому, что мы ввели его в рассмотрение, определив через изменение энергии при изменении значения обобщенной координаты модели
называется потому, что мы ввели его в рассмотрение, определив через изменение энергии при изменении значения обобщенной координаты модели 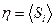 , но не вычислили, чему оно равно при той или иной температуре. Равновесные значения и определяются из так называемого уравнения состояния, которое представляет собой условие экстремума функции
, но не вычислили, чему оно равно при той или иной температуре. Равновесные значения и определяются из так называемого уравнения состояния, которое представляет собой условие экстремума функции 
 или
или  . (8)
. (8) есть единственная точка пересечения функции
есть единственная точка пересечения функции  y = th(Hsc / kT) и прямой
y = th(Hsc / kT) и прямой  . Она соответствует
. Она соответствует  , то есть
, то есть  , и магнитные моменты атомов неупорядочены. При
, и магнитные моменты атомов неупорядочены. При  появляются еще две точки пересечения, то есть еще два решения уравнения, которые соответствуют разным знакам равных по величине значений. Эти два решения соответствуют одной и той же упорядоченной фазе, в которой большая часть магнитных моментов атомов направлена либо вниз (
появляются еще две точки пересечения, то есть еще два решения уравнения, которые соответствуют разным знакам равных по величине значений. Эти два решения соответствуют одной и той же упорядоченной фазе, в которой большая часть магнитных моментов атомов направлена либо вниз ( ), либо вверх (
), либо вверх ( ). Это как бы два домена одной упорядоченной фазы. Области внешних условий на термостате (под ними следует понимать
). Это как бы два домена одной упорядоченной фазы. Области внешних условий на термостате (под ними следует понимать  и
и  ), при которых одно из описанных решений, соответствующее минимуму
), при которых одно из описанных решений, соответствующее минимуму  , определяется знаком второй производной
, определяется знаком второй производной  . Минимум соответствует
. Минимум соответствует  . Простые вычисления показывают, что, как только при изменении внешних условий появляются отличные от нуля решения уравнений состояния, они соответствуют минимуму
. Простые вычисления показывают, что, как только при изменении внешних условий появляются отличные от нуля решения уравнений состояния, они соответствуют минимуму  произошла бифуркация решений уравнения состояния.
произошла бифуркация решений уравнения состояния.
 начинается с того же приближения, что и приближение Вейса. Однако при подсчете вероятности состояния с данной энергией считается, что
начинается с того же приближения, что и приближение Вейса. Однако при подсчете вероятности состояния с данной энергией считается, что  , как и Е, определяется средним значением момента
, как и Е, определяется средним значением момента  ; здесь N - число узлов решетки (
; здесь N - число узлов решетки ( ), а
), а  и
и  - число моментов, направленных по и против внешнего поля:
- число моментов, направленных по и против внешнего поля:  . Ясно, что число способов размещения
. Ясно, что число способов размещения 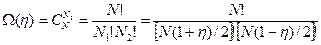 .
.
 .
. .
. , по виду несколько отличается от уравнения для определения самосогласованного поля в приближении Вейса
, по виду несколько отличается от уравнения для определения самосогласованного поля в приближении Вейса . (9)
. (9) - это функция, обратная
- это функция, обратная  , легко показать, что в приближении парных взаимодействий ответы для этих двух приближений совпадают.
, легко показать, что в приближении парных взаимодействий ответы для этих двух приближений совпадают. для обеих фаз. Вопрос аналитического сравнения
для обеих фаз. Вопрос аналитического сравнения  и
и  для этих моделей выходит за рамки нашего курса. Можно показать, что для обоих методов вычисления F модели Изинга-Ленца из равенства
для этих моделей выходит за рамки нашего курса. Можно показать, что для обоих методов вычисления F модели Изинга-Ленца из равенства  следует
следует  , но
, но  .
. это среднее дается стандартным выражением
это среднее дается стандартным выражением . (1)
. (1)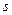 степенями свободы может быть математически представлено в виде точки в воображаемом
степенями свободы может быть математически представлено в виде точки в воображаемом  -мерном пространстве, по координатным осям которого откладываются обобщенные координаты и импульсы. Это воображаемое
-мерном пространстве, по координатным осям которого откладываются обобщенные координаты и импульсы. Это воображаемое  обозначать просто
обозначать просто  . Аналогично, запись
. Аналогично, запись  будем обозначать
будем обозначать  . Тогда элементарный объем
. Тогда элементарный объем  фазового пространства будет обозначаться
фазового пространства будет обозначаться  .
. . Можно утверждать, что за достаточно большой промежуток времени
. Можно утверждать, что за достаточно большой промежуток времени  - часть полного времени
- часть полного времени  будет стремиться к некоторому конечному пределу
будет стремиться к некоторому конечному пределу . (2)
. (2) состояний, которые изображаются точками внутри элементарного фазового объема, т.е. вероятность того, что обобщенные координаты
состояний, которые изображаются точками внутри элементарного фазового объема, т.е. вероятность того, что обобщенные координаты  и импульсы
и импульсы  лежат в заданных интервалах между
лежат в заданных интервалах между  ,
, 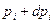 . Эту вероятность можно представить в виде
. Эту вероятность можно представить в виде . (3)
. (3) зависит от всех координат и импульсов подсистемы и играет роль плотности вероятности нахождения подсистемы в данной точке ее фазового пространства. Эта функция называется функцией статистического распределения или, как часто говорят, просто функцией распределения.
зависит от всех координат и импульсов подсистемы и играет роль плотности вероятности нахождения подсистемы в данной точке ее фазового пространства. Эта функция называется функцией статистического распределения или, как часто говорят, просто функцией распределения. , (4)
, (4) и импульсов
и импульсов  ). Соответственно, мы также можем вычислить и среднее значение любой такой величины. Оно получатся путем умножения всех возможных значений данной величины на соответствующие вероятности и интегрирования по всем состояниям. Другими, словами среднее значение величины
). Соответственно, мы также можем вычислить и среднее значение любой такой величины. Оно получатся путем умножения всех возможных значений данной величины на соответствующие вероятности и интегрирования по всем состояниям. Другими, словами среднее значение величины  , (5)
, (5) построить функцию распределения вероятностей различных значений величины
построить функцию распределения вероятностей различных значений величины  , будучи сколько-либо заметно отличной от нуля лишь в самой непосредственной близости к точке максимума (рис.1).
, будучи сколько-либо заметно отличной от нуля лишь в самой непосредственной близости к точке максимума (рис.1).
 и
и  . Обобщенные координаты и импульсы второй подсистемы будем, соответственно, обозначать
. Обобщенные координаты и импульсы второй подсистемы будем, соответственно, обозначать  и
и  . Функция распределения первой подсистемы
. Функция распределения первой подсистемы 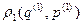 зависит только от ее координат и импульсов
зависит только от ее координат и импульсов  также зависит только от ее координат и импульсов
также зависит только от ее координат и импульсов 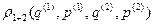 составной подсистемы “1+2”, т.е. подсистемы, представляющей собой объединение подсистемы 1 и подсистемы 2, зависит только от
составной подсистемы “1+2”, т.е. подсистемы, представляющей собой объединение подсистемы 1 и подсистемы 2, зависит только от  и
и  ее фазового пространства, который окружает точку
ее фазового пространства, который окружает точку  . Второе событие состоит в том, что подсистема 2 находится в объеме
. Второе событие состоит в том, что подсистема 2 находится в объеме  ее фазового пространства, который окружает точку
ее фазового пространства, который окружает точку  . Так вот, эти два события являются независимыми с точки зрения теории вероятности, т.е. вероятность того, что оба эти события произойдут одновременно, равна произведению вероятности первого события и вероятности второго события. Другими словами, вероятность того, что составная система “1+2” находится в элементе ее фазового пространства
. Так вот, эти два события являются независимыми с точки зрения теории вероятности, т.е. вероятность того, что оба эти события произойдут одновременно, равна произведению вероятности первого события и вероятности второго события. Другими словами, вероятность того, что составная система “1+2” находится в элементе ее фазового пространства 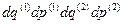 , который окружает точку
, который окружает точку 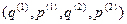 , равна произведению вероятности первой системе находиться в элементарном объеме
, равна произведению вероятности первой системе находиться в элементарном объеме  ее фазового пространства
ее фазового пространства  , (6)
, (6) , (7)
, (7)
 , относящуюся ко всему изучаемому телу или его отдельной макроскопической части. Эта величина будет с течением времени изменяться, колеблясь около своего среднего значения. Введем величину, характеризующую в среднем ширину интервала этого изменения. На первый взгляд, казалось бы, в качестве такой характеристики следует взять среднее значение разности
, относящуюся ко всему изучаемому телу или его отдельной макроскопической части. Эта величина будет с течением времени изменяться, колеблясь около своего среднего значения. Введем величину, характеризующую в среднем ширину интервала этого изменения. На первый взгляд, казалось бы, в качестве такой характеристики следует взять среднее значение разности  между самой величиной и ее средним значением. Однако среднее этой разности служить такой характеристикой не может, поскольку для макроскопической системы это среднее всегда равно нулю, независимо от того сколь часто наша величина
между самой величиной и ее средним значением. Однако среднее этой разности служить такой характеристикой не может, поскольку для макроскопической системы это среднее всегда равно нулю, независимо от того сколь часто наша величина  . (8)
. (8) . В результате получаем
. В результате получаем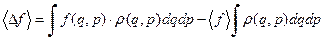 . (9)
. (9) (11)
(11) . По определению это среднее есть
. По определению это среднее есть . (12)
. (12) называется средней квадратичной флуктуацией величины
называется средней квадратичной флуктуацией величины  . (13)
. (13) . (14)
. (14) , получаем
, получаем . (15)
. (15) . (16)
. (16) называют относительной флуктуацией величины
называют относительной флуктуацией величины 


