
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 13. Магнитные свойства вещества. Парамагнетизм газов и электронов проводимости в металлах и полупроводниках.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Учение о магнитных свойствах веществ (магнетиков) весьма обширно, и мы остановимся только на некоторых основных понятиях. Если поместить тело во внешнее магнитное поле, то каждый элемент его объема
Намагниченность или магнитный момент единицы объема
Называется магнитной восприимчивостью вещества. Она зависит от вещества, температуры, давления, но не зависит от магнитного поля Если в разложении
Легко видеть, что Мы различаем: 1) Парамагнитные вещества, для которых Шелочные металлы тоже парамагнитны: но для них 2) Диамагнитные вещества, для которых 3) Ферромагнитные вещества (железо, кобальт, никель и ряд сплавов). Выше некоторой температуры, называемой температурой Кюри и равной для Fe, Co и Ni соответственно 1040, 1404 и 631 К, ферромагнитные вещества ведут себя как парамагнетики. Ниже температуры Кюри ферромагнетики обладают рядом интересных особенностей: в чистых монокристаллах уже слабое магнитное поле вызывает в определенных кристаллографических направлениях очень большую намагниченность Выведем для магнетиков некоторые простые термодинамические соотношения. Напряженность магнитного поля в нашей задаче является внешним параметром. Найдем обобщенную силу, отвечающую этому внешнему параметру. Для этого нам нужно вспомнить выражение для работы, совершаемой изотропной системой с магнитным моментом
Здесь M – проекция магнитного момента на направление магнитного поля. Следовательно, обобщенная сила, отвечающая модулю напряженности магнитного поля, есть проекция среднего магнитного момента нашего газа на направление магнитного поля. Таким образом, проекция среднего магнитного момента нашего газа на направление магнитного поля есть
Тогда в соответствии с (2) магнитная восприимчивость
Итак, для того, чтобы найти магнитный момент и магнитную восприимчивость, нам нужно найти свободную энергию и продифференцировать ее по магнитному полю. Рассмотрим теорию намагниченности вещества, состоящего из свободно вращающихся частиц (молекул) с постоянными магнитными моментами
где
где Среднее значение проекции магнитного момента
Интеграл в знаменателе берется элементарно, а интеграл в числителе равен производной по
где функция Ланжевена
Для слабых магнитных полей, когда
В этом случае намагниченность
Откуда магнитная восприимчивость
Мы видим, что в соответствии с законом Кюри В квантовой теории парамагнетизма атомов и ионов необходимо учесть два важных обстоятельства: дискретность пространственного квантования момента количества движения электрона и наличие у него спина. Как мы знаем из курса квантовой механики, если электрон в атоме находится в стационарном состоянии с определенной проекцией момента количества движения (орбитального момента)
- магнетон Бора – элементарный (наименьший) магнитный момент, фигурирующий в квантовой теории. Таким образом, для орбитального движения электрона
Такое же значение имеет отношение этих величин в классической теории. Теория и опыт показывают, что свободный электрон обладает магнитным моментом, равным магнетону Бора Для спина отношение Складывая векторно магнитные и вращательные моменты орбитального движения и спина, легко понять, что в силу «аномальности» отношения Это обстоятельство служит причиной аномального эффекта Зеемана. Можно показать, что в результате прецессии результирующего магнитного момента вокруг результирующего вращательного момента в направлении последнего возникает эффективный магнитный момент
где
- множитель Ландэ. Здесь Во внешнем магнитном поле
Среднее значение магнитного момента в направлении поля
где Рассмотрим для простоты случай слабых магнитных полей, когда
так что магнитная восприимчивость равна
где эффективный магнитный момент Рассмотрим теперь магнитные свойства газа электронов проводимости. Постановка задачи остается прежней, однако теперь изучим ситуацию, когда газ находится во внешнем стационарном однородном магнитном поле В соответствие с общим алгоритмом, прежде всего, найдем одночастичные стационарные состояния. Для этого мы должны решить стационарное уравнение Шредингера для одного отдельно взятого электрона с эффективной массой В отсутствие магнитного поля одноэлектронный оператор Гамильтона внутри объема газа есть просто оператор кинетической энергии
Вспомним, как выглядит Гамильтониан Прежде всего, определимся с выбором системы координат. В задаче есть выделенное направление – направление магнитного поля Магнитное поле дает два вклада в Гамильтониан электрона. Во-первых, рассматривая электрон в магнитном поле, мы должны в операторе кинетической энергии оператор импульса Во-вторых, как известно из релятивистской квантовой механики, наличие у электрона спина приводит к появлению у него собственного магнитного момента, не связанного с его движением в пространстве. Если электрон поместить в магнитное поле, то возникает взаимодействие его собственного магнитного момента с полем. Это взаимодействие приводит к появлению в Гамильтониане электрона дополнительного члена
Здесь Таким образом, оператор Гамильтона электрона в магнитном поле имеет вид
Как легко видеть, оператор Гамильтона коммутирует с оператором
где
Координатная волновая функция
Второй вклад
Вклад магнитного поля
где обозначено
Уравнение (30) в точности совпадает с одноэлектронным уравнением Шредингера в отсутствие магнитного поля. Таким образом, если мы пренебрежем первым вкладом магнитного поля, то координатная часть волновой функции электрона в магнитном поле останется той же самой, что и в ее отсутствие. Соответственно, в таком приближении одночастичное стационарное состояние задается спиновым квантовым числом
а вот энергия одноэлектронного состояния
Таким образом, взаимодействие собственного магнитного момента электрона с магнитным полем приводит к снятию вырождения одноэлектронных уровней энергии по проекции спина – энергии одночастичных состояний с одним и тем же значением волнового вектора
и
Если теперь мы учтем первый вклад магнитного поля
и
Здесь
где Как хорошо видно, вклад магнитного поля Итак, магнитное поле дает два вклада в Гамильтониан. Первый вклад Теперь разберемся, как каждый из этих вкладов сказывается на магнитных свойствах электронного газа. Начнем со второго вклада, обусловленного взаимодействием собственного магнитного момента электрона с магнитным полем. Для того, чтобы лучше понять его роль, для начала полностью пренебрежем квантованием Ландау, т.е. полностью пренебрежем вкладом магнитного поля Наша задача состоит в том, чтобы вычислить в этом приближении вычислить средний магнитный момент газа Магнитный момент всего газа складывается из собственных магнитных моментов электронов. Как известно из квантовой механики, собственный магнитный момент электрона может быть направлен либо по полю, либо против поля. Причем в обоих случаях модуль магнитного момента равен магнетону Бора Собственный магнитный момент электрона, находящегося в одночастичном состоянии с квантовым числом Собственный магнитный момент электрона, находящегося в одночастичном состоянии с квантовым числом Следовательно, проекция среднего магнитного момента газа на направление поля есть
Таким образом, наша задача свелась к нахождению среднего числа Эта величина
Подставляя явный вид (125) одноэлектронных уровней энергии, получаем
Введем в рассмотрение функцию
Значение этой функции, очевидно, есть половина числа частиц в свободном электронном газе с химическим потенциалом
Рассмотрим случай
Соответственно, среднее число электронов в одночастичных состояниях с
среднее число электронов в одночастичных состояниях с
Как хорошо видно, при Магнитное же поле приводит к перераспределению электронов по одночастичным состояниям с различным значением проекции спина. Поскольку
становится положительным. Соответственно, магнитный момент газа сонаправлен с магнитным полем, что соответствует парамагнетизму. Таким образом, взаимодействие собственного магнитного момента электрона с магнитным полем приводит к парамагнетизму электронного газа. Найдем магнитную восприимчивость вырожденного газа электронов проводимости в металле. Как мы получали ранее, в этом случае
Тогда
Таким образом, магнитная восприимчивость единицы объема
Воспользовавшись полученным ранее выражением для химического потенциала вырожденного электронного газа, получаем с точностью до членов
где Мы видим, что главная часть парамагнитной восприимчивости электронов проводимости металла, в соответствии с опытом, не зависит от температуры. Малая температурная поправка к Для невырожденных электронов проводимости полупроводника ситуация иная. В этом случае
Соответственно,
Таким образом, для магнитной восприимчивости невырожденных электронов проводимости полупроводника получаем
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 470; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.11.13 (0.014 с.) |

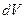 приобретет магнитный момент
приобретет магнитный момент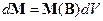 . (1)
. (1)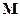 зависит от величины и направления напряженности магнитного поля
зависит от величины и направления напряженности магнитного поля 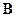 . В изотропных телах
. В изотропных телах 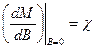 (2)
(2)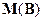 в ряд по
в ряд по 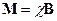 . (3)
. (3)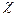 безразмерна.
безразмерна.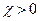 , т.е.
, т.е. 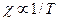 (закон Кюри). При комнатной температуре и атмосферном давлении
(закон Кюри). При комнатной температуре и атмосферном давлении 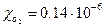 .
.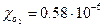 .
.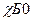 , т.е.
, т.е. 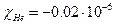 .
.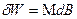 . (4)
. (4)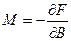 . (5)
. (5)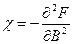 . (6)
. (6)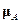 (теория парамагнитного газа Ланжевена). Магнитное поле
(теория парамагнитного газа Ланжевена). Магнитное поле 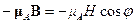 , где
, где 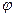 - угол между
- угол между  и
и 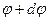 , равна
, равна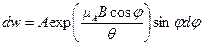 , (7)
, (7)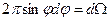 - телесный угол, соответствующий интервалу угла
- телесный угол, соответствующий интервалу угла 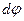 , а
, а 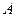 - константа, определяемая из условия нормировки вероятности
- константа, определяемая из условия нормировки вероятности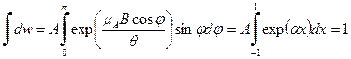 , (8)
, (8)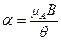 и
и 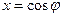 .
.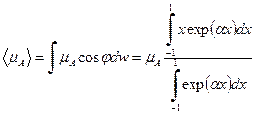 . (9)
. (9)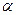 от интеграла в знаменателе. Таким образом,
от интеграла в знаменателе. Таким образом,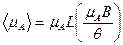 . (10)
. (10)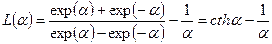 . (11)
. (11)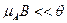 , т.е.
, т.е. 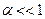 , разлагая правую часть (11) в ряд, получим
, разлагая правую часть (11) в ряд, получим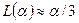 . (12)
. (12)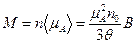 . (13)
. (13)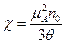 . (14)
. (14)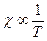 .
.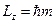 (где
(где 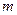 - магнитное квантовое число), то этому состоянию соответствует магнитный момент
- магнитное квантовое число), то этому состоянию соответствует магнитный момент 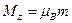 , где
, где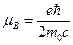 (15)
(15)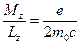 . (16)
. (16)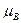 , и вращательным моментом, проекции которого на заданное направление равны
, и вращательным моментом, проекции которого на заданное направление равны 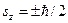 . Эти свойства электрона получили названия спина.
. Эти свойства электрона получили названия спина.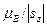 имеет «аномальное», вдове большее значение, чем (16).
имеет «аномальное», вдове большее значение, чем (16).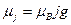 , (17)
, (17)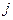 - квантовое число полного вращательного момента, равного
- квантовое число полного вращательного момента, равного 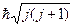 , а
, а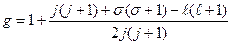 (18)
(18)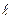 - квантовое число орбитального вращательного момента, равного
- квантовое число орбитального вращательного момента, равного 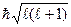 , а
, а  - спиновое квантовое число, принимающее два значения:
- спиновое квантовое число, принимающее два значения: 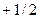 и
и 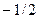 .
.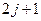 дискретных ориентаций, образуя с магнитным полем углы
дискретных ориентаций, образуя с магнитным полем углы 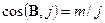 ,
, 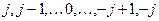 . Энергия магнитного момента
. Энергия магнитного момента 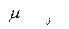 в магнитном поле равна
в магнитном поле равна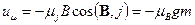 . (19)
. (19)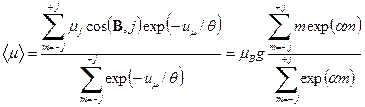 , (20)
, (20)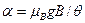 .
.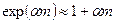 . В этом случае из (20) получаем
. В этом случае из (20) получаем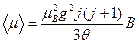 , (21)
, (21)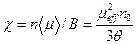 , (22)
, (22)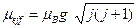 . Мы видим, что и в квантовом случае магнитная восприимчивость обратно пропорциональна температуре.
. Мы видим, что и в квантовом случае магнитная восприимчивость обратно пропорциональна температуре.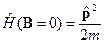 . (23)
. (23)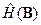 электрона в магнитном поле.
электрона в магнитном поле.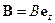 , где
, где 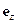 - орт оси z.
- орт оси z.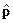 заменить разностью
заменить разностью 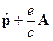 . Здесь
. Здесь 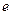 - абсолютная величина заряда электрона,
- абсолютная величина заряда электрона, 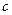 - скорость света,
- скорость света, 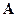 - векторный потенциал магнитного поля.
- векторный потенциал магнитного поля.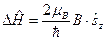 . (24)
. (24)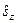 - оператор проекции спина электрона на ось z, т.е. на направление магнитного поля.
- оператор проекции спина электрона на ось z, т.е. на направление магнитного поля.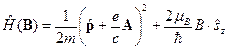 . (25)
. (25)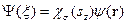 , (26)
, (26)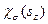 - собственная функция оператора проекции спина, отвечающая собственному значению
- собственная функция оператора проекции спина, отвечающая собственному значению 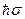 :
: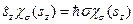 . (27)
. (27)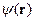 определяется одночастичным стационарным уравнением Шредингера
определяется одночастичным стационарным уравнением Шредингера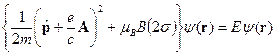 . (28)
. (28)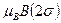 не зависит от координат. Перенесем его направо
не зависит от координат. Перенесем его направо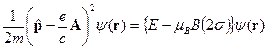 . (29)
. (29)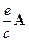 приводит к квантованию движения электрона, которое носит название квантования Ландау. Если мы пренебрежем этим вкладом, то наше уравнение Шредингера примет вид
приводит к квантованию движения электрона, которое носит название квантования Ландау. Если мы пренебрежем этим вкладом, то наше уравнение Шредингера примет вид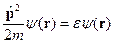 , (30)
, (30)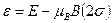 . (31)
. (31) . Одноэлектронная волновая функция состояния
. Одноэлектронная волновая функция состояния 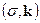 имеет тот же самый вид, что и в отсутствие поля
имеет тот же самый вид, что и в отсутствие поля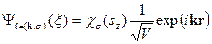 , (32)
, (32)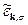 отличается от энергии
отличается от энергии 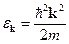 свободного электрона на величину
свободного электрона на величину 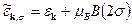 . (33)
. (33)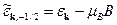 . (34)
. (34)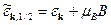 . (35)
. (35)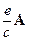 , то структура координатной части одноэлектронной волновой функции и структура одночастичного энергетического спектра качественно изменятся. В калибровке Ландау
, то структура координатной части одноэлектронной волновой функции и структура одночастичного энергетического спектра качественно изменятся. В калибровке Ландау 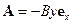 одноэлектронные стационарные состояния задаются спиновым квантовым числом
одноэлектронные стационарные состояния задаются спиновым квантовым числом 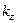 волнового вектора на направление магнитного поля, проекцией
волнового вектора на направление магнитного поля, проекцией 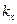 волнового вектора на декартову ось х, лежащую в плоскости, перпендикулярной напряженности магнитного поля, а также целым положительным числом
волнового вектора на декартову ось х, лежащую в плоскости, перпендикулярной напряженности магнитного поля, а также целым положительным числом 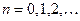 , которое называется номером уровня Ландау. Нормированная волновая функция и энергия одноэлектронного стационарного состояния с квантовыми числами
, которое называется номером уровня Ландау. Нормированная волновая функция и энергия одноэлектронного стационарного состояния с квантовыми числами 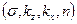 соответственно имеют вид
соответственно имеют вид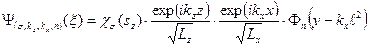 , (36)
, (36)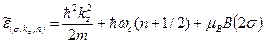 . (37)
. (37)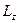 - линейный размер по оси z объема, содержащего наш электронный газ,
- линейный размер по оси z объема, содержащего наш электронный газ, 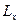 - линейный размер этого объема по оси х. Второе слагаемое
- линейный размер этого объема по оси х. Второе слагаемое 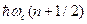 в выражении для энергии и функция
в выражении для энергии и функция 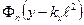 есть n-ый уровень энергии и отвечающая ему волновая функция линейного гармонического осциллятора с циклотронной частотой
есть n-ый уровень энергии и отвечающая ему волновая функция линейного гармонического осциллятора с циклотронной частотой 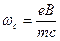 и положением равновесия
и положением равновесия 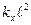 , где
, где 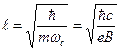 - магнитная длина. Волновая функция n-го уровня энергии нашего осциллятора, напомню, имеет вид
- магнитная длина. Волновая функция n-го уровня энергии нашего осциллятора, напомню, имеет вид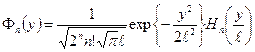 , (38)
, (38)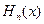 - полином Эрмита.
- полином Эрмита.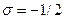 , направлен по полю. Соответственно, проекция магнитного момента такого электрона на ось z равна
, направлен по полю. Соответственно, проекция магнитного момента такого электрона на ось z равна 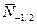 .
.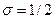 , направлен против поля. Соответственно, проекция магнитного момента такого электрона на ось z равна
, направлен против поля. Соответственно, проекция магнитного момента такого электрона на ось z равна 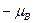 . Среднее число электронов со спиновым квантовым числом
. Среднее число электронов со спиновым квантовым числом 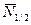 .
.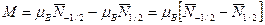 . (39)
. (39)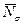 электронов в одночастичных состояниях с данным значением спинового квантового числа
электронов в одночастичных состояниях с данным значением спинового квантового числа 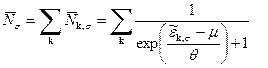 . (40)
. (40)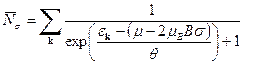 . (41)
. (41)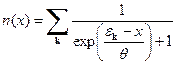 . (42)
. (42)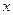 . тогда
. тогда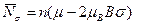 . (43)
. (43)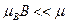 . В этом случае функцию (43) можно разложить в ряд Тейлора в окрестности точки
. В этом случае функцию (43) можно разложить в ряд Тейлора в окрестности точки  . Ограничимся в этом разложении первой поправкой по магнитному полю
. Ограничимся в этом разложении первой поправкой по магнитному полю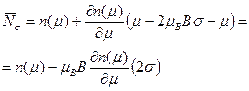 . (44)
. (44)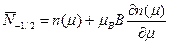 , (45)
, (45)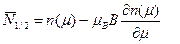 . (46)
. (46)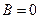 среднее число электронов в одночастичных состояниях с
среднее число электронов в одночастичных состояниях с 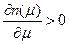 , электронов с магнитным моментом, сонаправленным с полем, становится больше, чем электронов с противоположным направлением собственного магнитного момента. В результате проекция среднего магнитного момента на направление поля
, электронов с магнитным моментом, сонаправленным с полем, становится больше, чем электронов с противоположным направлением собственного магнитного момента. В результате проекция среднего магнитного момента на направление поля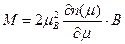 . (47)
. (47)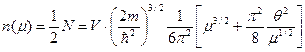 . (48)
. (48)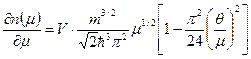 . (49)
. (49)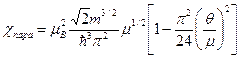 . (50)
. (50)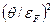
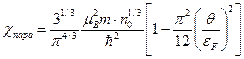 , (51)
, (51)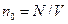 - концентрация электронов проводимости металла.
- концентрация электронов проводимости металла.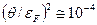 .
.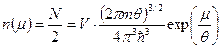 . (52)
. (52)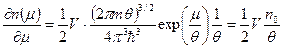 . (53)
. (53)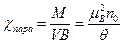 , (54)
, (54)


