
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 7. Вырожденный идеальный бозе-газ. Бозе-конденсация. Равновесное тепловое излучение.Содержание книги
Поиск на нашем сайте
Рассмотрим газ из N невзаимодействующих тождественных бозонов с отличной от нуля массой покоя в объеме V в отсутствие внешних силовых полей. Как мы знаем из курса квантовой механики, в этом случае одночастичный базис может быть сформирован из произведения собственных функций оператора проекции спина на плоские волны
Таким образом, в нашем случае одночастичное стационарное состояние задается волновым вектором
Поскольку мы имеем дело с макроскопической системой, то аналогично тому, как мы поступали в курсе квантовой механики при рассмотрении одноэлектронных состояний в идеальном кристалле, мы здесь можем использовать периодические граничные условия, и в дальнейшем аппроксимировать сумму по волновым векторам интегралом
Поскольку у нас имеет место вырождение по спину, то суммирование по спиновому квантовому числу везде приводет просто к умножению на число значений, которые может принимать спиновое квантовое число. Спиновое квантовое число для частицы со спином Среднее число частиц в одночастичном стационарном состоянии
Сумма
Как мы обращали внимание при выводе распределение Бозе-Эйнштейна, химический потенциал бозе-газа всегда
Согласно общефизическому принципу минимальности энергии в нашем бозе-газе при абсолютном нуле температуры реализуются только основные микросостояния. Поскольку в бозе-газе нет ограничения на числа заполнения одночастичных состояний, то в основном микросостоянии нашего газа все бозоны будут находится в одночастичном состоянии с самой маленькой энергией. Наименьшее значение энергии имеет одночастичное стационарное состояние
При увеличении температуры становится отличной от нуля также и вероятность возбужденных микросостояний. В этих микросостояниях часть электронов переходит с основного одночастичного стационарного состояния в возбужденные, т.е. в состояния с В основном одночастичном состоянии энергия равна нулю. Следовательно, среднее число бозонов в этом состоянии есть
Из (7) находим
Таким образом, мы видим, что при достаточно низких температурах, когда
Поэтому в этой сумме (3) для членов с
Заменяя сумму интегралом по
То, что в область интегрирования попадает точка
Как видно, подынтегральная функция в точке Теперь разумно провести обезразмеривающую замену переменной. За новую переменную в такой ситуации логично принять показатель экспоненты
После этой замены переменной наш интеграл принимает вид
Величина, стоящая в квадратных скобках, является константой. Обозначим ее Таким образом, получаем
где
Таким образом, мы видим, что по мере увеличения температуры число частиц в основном состоянии уменьшается и при температуре Таким образом, Явление накопления бозонов в основном одночастичном состоянии называется конденсацией Бозе-Эйнштейна. Соответственно, температура Рассмотрим равновесное тепловое излучение, заключенное в ящик в форме куба со стороной Из квантовой электродинамики известно, что Гамильтониан электромагнитного поля можно представить в виде суммы ЛГО за вычетом энергии нулевых колебаний
Каждый осциллятор соответствует одной из линейно поляризованных мод электромагнитного излучения, и, соответственно, задается значением волнового вектора Такие моды представляют собой плоские электромагнитные волны с электрическим вектором
Модуль вектора поляризации
Поскольку у нас излучение заключено в ящик, то его можно рассматривать как набор стоячих волн с узлами на стенках. Как известно, спектр волнового вектора в этом случае является дискретным и имеет вид
Таким образом, вычисление термодинамических характеристик РТИ сводится к вычислению термодинамических характеристик равновесной системы ЛГО. Последнюю задачу мы решали на практическом занятии. Поэтому воспользуемся готовым результатом. Только во всех выражениях мы должны убрать энергию нулевых колебаний. Таким образом, свободная энергия и внутренняя энергия РТИ есть
и
Среднее значение числа заполнения осциллятора
Из выражений (20-22) видно, что электоромагнитное излучение мы можем рассматривать как идеальный газ бозонов с волновыми векторами Воспользовавшись квазинепрерывностью спектра волнового вектора, перейдем в выражениях (20) и (21) от суммирования по волновым векторам к интегрированию, и также учтем, что суммируемые выражения не зависят от поляризации
и
Здесь мы также учли закон дисперсии (18). Поскольку подынтегральные выражения в (23) и (24) не зависят от направления волнового вектора, то эти интегралы разумно вычислять в сферической системе координат. Тогда интегрирования по углам даст полный телесный угол
и
Воспользовавшись законом дисперсии (18), в выражении (26) для внутренней энергии перейдем от интегрирования по волновым векторам к интегрированию по частотам
Выражение под знаком интеграла
представляет собой спектральную плотность излучения (энергию излучения, заключенную в данном участке спектра). Эта формула (28) для спектрального распределения энергии черного излучения называется формулой Планка. При малых частотах (
В обратном предельном случае больших частот (
Перейдя в интеграле (26) к безразмерной переменной
Коэффициент пропорциональности
называется постоянной Стефана-Больцмана. Поскольку электромагнитное поле обладает импульсом. Поэтому оно оказывает давление на стенку сосуда. Давление есть производная свободной энергии по объему
Перейдя в интеграле (11) к безразмерной переменной
Отсюда давление
Наконец, энтропия
|
|||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 685; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.186.225 (0.009 с.) |

 . (1)
. (1) и спиновым квантовым числом
и спиновым квантовым числом  . Одночастичные энергии даются выражением
. Одночастичные энергии даются выражением . (2)
. (2) . (3)
. (3)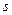 может принимать
может принимать  -о значение. Поэтому сейчас для сокращения записи будем считать, что спин у наших бозонов равен нулю. Тогда спиновое квантовое число может принимать только одно значение нуль, и соответственно, одночастичное стационарное состояние будет задаваться просто волновым вектором
-о значение. Поэтому сейчас для сокращения записи будем считать, что спин у наших бозонов равен нулю. Тогда спиновое квантовое число может принимать только одно значение нуль, и соответственно, одночастичное стационарное состояние будет задаваться просто волновым вектором  . (4)
. (4) по всем одночастичным стационарным состояниям равна полному числу частиц в нашем бозе-газе
по всем одночастичным стационарным состояниям равна полному числу частиц в нашем бозе-газе . (5)
. (5) . Для того, чтобы лишний раз в этом убедится, давайте посмотрим, что произойдет с распределением по одночастичным состояниям, если хим. потенциал будет положительный. В этом случае для одночастичных стационарных состояний с энергией
. Для того, чтобы лишний раз в этом убедится, давайте посмотрим, что произойдет с распределением по одночастичным состояниям, если хим. потенциал будет положительный. В этом случае для одночастичных стационарных состояний с энергией  показатель экспоненты является отрицательным Соответственно, сама экспонента
показатель экспоненты является отрицательным Соответственно, сама экспонента  меньше единицы. Таким образом, получается, что при положительном химическим потенциале число частиц в таких одночастичных стационарных состояниях является отрицательным. Таким образом, мы еще раз убеждаемся в том, что в нашем бозе-газе химический потенциал не может быть положительным.
меньше единицы. Таким образом, получается, что при положительном химическим потенциале число частиц в таких одночастичных стационарных состояниях является отрицательным. Таким образом, мы еще раз убеждаемся в том, что в нашем бозе-газе химический потенциал не может быть положительным.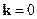 . Энергия этого одночастичного стационарного состояния равна нулю. Таким образом, при абсолютном нуле температуры функция распределения Бозе-Эйнштейна для нашего газа имеет вид
. Энергия этого одночастичного стационарного состояния равна нулю. Таким образом, при абсолютном нуле температуры функция распределения Бозе-Эйнштейна для нашего газа имеет вид . (6)
. (6) . Поэтому по мере увеличения температуры среднее число бозонов в основном одночастичном состоянии уменьшается. Соотвественно, среднее число бозонов в остальных, т.е. возбужденных одночастичных стационарных состояниях растет. Найдем, как с увеличением температуры изменяется среднее число бозонов в основном одночастичном состоянии.
. Поэтому по мере увеличения температуры среднее число бозонов в основном одночастичном состоянии уменьшается. Соотвественно, среднее число бозонов в остальных, т.е. возбужденных одночастичных стационарных состояниях растет. Найдем, как с увеличением температуры изменяется среднее число бозонов в основном одночастичном состоянии.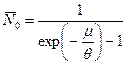 . (7)
. (7) . (8)
. (8) химический потенциал очень мал. Он приблизительно равен
химический потенциал очень мал. Он приблизительно равен . Более того, можно показать, что в такой ситуации химический потенциал мал даже по сравнению с первыми возбужденным уровнем энергии.
. Более того, можно показать, что в такой ситуации химический потенциал мал даже по сравнению с первыми возбужденным уровнем энергии. . (9)
. (9) . (10)
. (10) , и наш интеграл из трехмерного станет одномерным
, и наш интеграл из трехмерного станет одномерным . (11)
. (11) . (12)
. (12) . (13)
. (13) .
. , (14)
, (14) . (15)
. (15) , оно обращается в нуль. Можно показать, что оно остается нулем и при температуре
, оно обращается в нуль. Можно показать, что оно остается нулем и при температуре  .
. есть характерная температура, ниже которой начинается накопление частиц в основном одночастичном стационарном состоянии.
есть характерная температура, ниже которой начинается накопление частиц в основном одночастичном стационарном состоянии. .
. . (16)
. (16) . Частота осциллятора совпадает с частотой соответствующей моды.
. Частота осциллятора совпадает с частотой соответствующей моды. . (17)
. (17) . Направлен он перпендикулярно волновому вектору
. Направлен он перпендикулярно волновому вектору  связана с волновым вектором как
связана с волновым вектором как . (18)
. (18) .. (19)
.. (19) (20)
(20) . (21)
. (21) . (22)
. (22) и поляризацией
и поляризацией  (23)
(23) . (24)
. (24) . Таким образом,
. Таким образом, (25)
(25) . (26)
. (26) . (27)
. (27) . (28)
. (28) ) формула Планка переходит в формулу Рэлея-Джинса
) формула Планка переходит в формулу Рэлея-Джинса . (29)
. (29)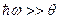 ) получаем формулу Вина
) получаем формулу Вина . (30)
. (30) , получаем закон Стефана-Больцмана
, получаем закон Стефана-Больцмана . (31)
. (31) . (32)
. (32) . (33)
. (33) . (34)
. (34) . (35)
. (35) . (36)
. (36)


