
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Окружающей среды. Внешние параметры. Теплообмен..Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теперь обсудим то, каким образом информация об окружающей среде входит в функцию распределения макроскопической системы, которая находящейся в равновесии с этой средой. Как обсуждалось на прошлой лекции, при описании макроскопического тела, находящегося в равновесии с окружающей средой, истинные значения всех его макроскопических характеристик можно с огромной точностью заменить на средние значения, которые получаются с помощью функции распределения, определенной таким образом, что она не зависит от микросостояния окружающей среды. Однако то обстоятельство, что функция распределения равновесной системы не зависит от микросостояния окружающей среды вовсе не означает, что эта функция вообще не содержит информацию об окружающей среде. Информация об окружающей среде в функции распределения, конечно же, присутствует. Однако присутствует она в виде параметрической зависимости от макроскопического состояния окружающей среды. Другими словами, функция распределения равновесной системы параметрически зависит от макроскопического состояния окружающей среды и не зависит от того, с помощью какого микросостояния это макросостояние окружающей среды реализуется. На языке термодинамики это означает, что информация о влиянии окружающей среды входит в функцию распределения изучаемого тела через параметрическую зависимость этой функции от внешних термодинамических параметров и температуры, которые задают состояние термодинамического равновесия, в котором находится наше тело. В данном состоянии термодинамического равновесия, т.е. при данных конкретных значениях внешних термодинамических параметров и температуры, явный вид функции распределения нашей системы вполне определенный. Однако если теперь поместить наше тело в другое состояние термодинамического равновесия, которое определяется другими значениями внешних термодинамических параметров или температуры, то явных вид функции распределения нашей системы изменится. Однако при этом в обоих состояния термодинамического равновесия, функция распределения нашей системы не будет зависеть от микросостояния окружающей среды. Конечно, если мы учтем влияние микроскопического состояния окружающей среды на распределение вероятности различных микросостояний нашего тела, то мы построим формально более точную теорию. Однако для нашей задачи практическая значимость этого уточнения будет фактически нулевой. Давайте теперь разбираться, что такое внешние и внутренние термодинамические параметры, и какова их роль в статистической теории Прежде всего, еще раз подчеркну, что мы различаем два понятия состояния макроскопической системы. Одно - это микроскопическое состояние. Другое - это состояние термодинамического равновесия, т.е. состояние макроскопическое. Задать микроскопическое состояние системы - значит указать все ее координаты и импульсы системы. Такой способ описания состояния системы является максимально подробным. Однако, как мы уже обсуждали, для практических приложений столь подробное описание состояния макроскопической системы является излишним. Дело в том, что, как правило, на практике мы имеем дело с макроскопическими параметрами, т.е. с измеряемыми с помощью макроскопических приборов величинами, такими как объем, давление, температура, плотность, концентрация, упругость, намагниченность, поляризация и т.п. Поэтому на практике состояние макроскопических тел, как правило, характеризуется этими макроскопическими параметрами. Охарактеризованное таким способом состояние макроскопической системы называется макроскопическим состоянием. По самому своему смыслу макроскопические параметры огрублено (усреднено) характеризуют макроскопическую систему. Рассмотрим простейший пример – сосуд с разреженным газом, помещенный в термостат. Состояние термодинамического равновесия этого газа задается двумя макроскопическими параметрами: внешним термодинамическим параметром – объемом сосуда и температурой термостата. Понятно, что точная микроскопическая картина взаимодействия частиц газа с атомами стенки сосуда является необычайно сложной. Для строго описания такой картины нужно учесть структуру вещества стенки, тепловые колебания атомов стенки, квантовомеханические особенности взаимодействия частиц газа с атомами стенки, причем мы должны учесть именно взаимодействие, т.е. взаимное влияние атомов стенки и частиц газа на состояние друг друга, ну и т.д. Однако для практических приложений столь подробно описывать влияние стенки на газ нет никакой необходимости. Достаточно поступить следующим образом. Всю сложную структуру стенки сосуда можно с огромной точностью заменить жесткой неизменной во времени математической поверхностью, непроницаемой для молекул газа. Внешний параметр – объем газа является функцией координат точек этой поверхности, которая имитирует внешнее по отношению к нашему газу тело – стенку сосуда. Причем эта поверхность и, соответственно, объем никак не зависит от координат и импульсов молекул газа. С точки зрения математического аппарата статистической теории, проводя такое огрубление стенки сосуда, мы очень сложное взаимодействие газа и стенки приближенно учитываем, рассматривая наш газ во внешнем потенциале следующего вида
Другими словами, мы влияние стенки на аппроксимируем внешним по отношению к нашу газу силовым полем с данным потенциалом. Таким образом, мы нашему разреженному газу приписываем эффективную функцию Гамильтона
которая есть кинетическая энергия газа плюс потенциальная энергия газа во внешнем силовом поле, которое моделирует влияние стенки сосуда на газ. Это внешнее силовое поле определяется внешним параметром – объемом. Поэтому эффективный гамильтониан нашего газа параметрически зависит от объема. Обращаю ваше внимание, что независимыми переменными в этом гамильтониане являются координаты и импульсы только нашего газа. Однако, включив в этот Гамильтониан второе слагаемое, мы учли все существенное влияние на наш газ окружающей среды, которое можно с большой точностью аппроксимировать чисто силовым внешним воздействием. Это внешнее силовое поле определяется внешним параметром – объемом. Поэтому эффективный гамильтониан нашего газа параметрически зависит от объема. Однако при описании нашего газа помимо влияния стенки сосуда мы еще обязательно должны учесть теплообмен между газом и термостатом. При этом нужно иметь ввиду, что теплообмен между системой и окружающей средой принципиально нельзя свести к внешнему силовому воздействию на изучаемую систему. Другими словами, влияние теплообмена на газ принципиально нельзя учесть, рассмотрев наш газ в неком внешнем силовом поле. Вообще, любое действие есть аппроксимация некого взаимодействия. Если говорить строго, то в природе не бывает действия, бывает только взаимодействие. Другими словами, любые две системы влияют на состояние друг друга самосогласованным образом. Когда мы говорим о внешнем поле, приложенном к изучаемой системе, то это всегда приближение. В качестве примера рассмотрим свободное падение тела в поле тяготения Земли. Строго говоря, тело и Землей взаимодействуют. Поэтому состояние тела и состояние Земли меняются самосогласованным образом. Однако масса тела ничтожна по сравнению с массой Земли. Поэтому влиянием состояния маркера на состояние Земли можно пренебречь, и считать, что движение маркера происходит во внешнем силовом поле – поле тяжести Теперь, опираясь на данный пример, поймем суть того, как в статистической теории и, соответственно, в термодинамике учитывается теплообмен между изучаемой макроскопической системой и окружающей средой. Прежде всего, вспомним, что согласно постановке задачи наш газ и термостат вместе образует замкнутую систему. При этом наша система очень мала по сравнению с термостатом, так что влияние нашей системы на термодинамическое состояние термостата пренебрежимо мало. Для краткости всю совокупность координат нашего газа обозначим По определению энергия замкнутой системы не меняется. Функция Гамильтона системы есть ее полная энергия, рассмотренная как функция ее координат и импульсов. Следовательно, функция Гамильтона всей замкнутой системы “наш газ+термостат” При попытке учесть взаимодействие нашего газа с термостатом, используя методы обычной механики, мы сталкиваемся с еще большей проблемой. Мало того, что наша система имеет огромное число степеней свободы, так вообще мы обязаны применять аппарат обычной механики ко всей замкнутой системе Действительно, функция Гамильтона совокупности “наша система+термостат”, вообще говоря, содержит три члена - функцию Гамильтона нашей системы
Причем третий член описывает именно взаимодействие. Его нельзя представить в виде суммы двух функций, одна из которых зависит от микросостояния только нашей системы, а другая – от микросостояния только окружающей среды. Уравнения Гамильтона в этом случае имеют вид
Индекс пробегает значения Из-за наличия третьего члена Точный вид члена
Однако при такой аппроксимации мы вовсе не исключаем из нашей задачи возможность обмена энергией между нашим газом и термостатом. Мы просто пользуемся тем обстоятельством, что энергия взаимодействия хотя и отлична от нуля, но настолько мала, что при вычислении энегии всей системы ею можно пренебречь на фоне больших значений энергий газа и термостата. Когда мы задаем состояние равновесия замкнутой системы “наш газ+термостат”, то мы фиксируем энергию всей этой замкнутой системы Указанная аппроксимация гамильтониана является одним из основных моментов, используемых при решении задачи о функции распределения нашего газа. В дальнейшем мы непосредственно увидим, что функция распределения нашего газа имеет следующий вид
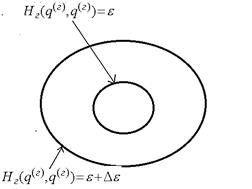
Здесь Заметим, что эта температура определяется, строго говоря, равновесным состоянием всей замкнутой системы, а именно – ее энергией Е. Но поскольку наш газ представляет собой очень малую по сравнению с термостататом систему, то энергия Е определяется главным образом энергией термостата. Следовательно, и температура Т определяется главным образом термостатом. Именно это имеют ввиду, когда говорят “температура термостата”. Глядя на выписанную формулу для функции распределения нашего газа, легко видеть, что различные значения энергии нашей системы могут реализовываться с различной вероятностью, которая определяется температурой Т. Для того, чтобы сказанное было еще нагляднее, найдем вероятность того, что энергия нашего газа лежит в элементарном интервале от Рассмотрим в фазовом пространстве нашего газа две поверхности постоянной энергии. Одна изоэнергетическая поверхность определяется уравнением
Рис.1
Давайте найдем объем фазового пространства между этими двумя изоэнергетическими поверхностями. Обозначим
объем фазового пространства, ограниченный изоэнергетической поверхностью
У нас Таким образом, мы пишем
Сокращая одинаковые члены, получаем
Если мы теперь устремим
Теперь мы можем написать одну очень полезную на практике формулу. Пусть
где
Давайте теперь функцию распределения нашего газа проинтегрируем по его объему между изоэнергетическим поверхностями
Этот интеграл есть вероятность того, что энергия нашего газа лежит в интервале от Действительно. Рассмотрим в качестве элементарного событие, состоящее в том, что наш газ находится в конкретном элементарном объеме своего фазового пространства. Два различных таких события, понятно, не могут произойти одновременно. События, которые не могут произойти одновременно, в теории вероятности называются несовместными. В теории вероятности имеется так называемая теорема о сложении вероятности. Смысл этой теоремы состоит в следующем. Пусть у нас имеются два несовместных события. Обозначим одно событие цифрой 1, его вероятность обозначим
Возвращаемся к нашему газу. Рассмотрим два элементарных события. Первое событие состоит в том, что наш газ находится в элементарном объеме его фазового пространства, окружающем точку
Интеграл есть аналог суммы в ситуации, когда суммируемые величины меняются непрерывно. Таким образом, если мы проинтегрируем функцию распределения нашего газа между двумя этими изоэнергетическими поверхностями, то мы получим вероятность того, что наш газ находится в какой-то из точек, лежащей между этими поверхностями постоянной энергии. Но в любой из этих точек фазового пространства энергия газа лежит в интервале от Подставим явный вид функции распределения и воспользуемся соотношением (15). В результате получим
Отсюда вероятность того, что энергия нашего газа лежит в интервале от
Теперь уже совмем четко видно, что наш гах может иметь не одну определенную энергию, а с определенной вероятностью ряд значений энергии. Причем распределение вероятностей различных значений энергии определяется температурой термостата. Вернемся теперь к выражению для функции распределения нашего газа. Из этого выражения видно, что функция распределения нашего газа зависит только от его координат и импульсов, и не зависит от микросостояния окружающей среды. Информация об окружающей среде входит в эту функцию распределения нашего газа через параметрическую зависимость от внешнего параметра - объема и от температуры термостата, которые задают его конкретное состояние термодинамического равновесия. В данном состоянии термодинамического равновесия, т.е. при заданном значении объема и температуры, явный вид функции распределения нашей системы вполне определенный. Однако, если теперь поместить нашу систему в другое состояние термодинамического равновесия, которое определяется другими значениями объема или температуры, то явных вид функции распределения нашей системы изменится. Однако при этом в обоих состояния термодинамического равновесия, функция распределения нашего газа не зависит от микросостояния окружающей среды. Далее среднее значение любой функции
Из этого выражения видно, что любой внутренний параметр Отсюда как раз и следует, что состояние равновесия нашего газа задается двумя термодинамическими параметрами – объемом и температурой. Теперь те основные моменты, с которыми мы разобрались на данном конкретном примере, сформулируем для общего случая. Прежде всего, еще раз подчеркнем, что в дальнейшем мы всегда будем иметь дело с макроскопическими системами, находящимися в равновесии с окружающей средой. Когда мы будем говорить о термодинамических процессах, то мы всегда будем рассматривать квазистатические обратимые процессы. Напомню, что процесс называется квазистатическим, если внешние условия изменяются настолько медленно, что в любой момент времени систему можно описать так, как если бы она находилась в состоянии термодинамического равновесия. Другими словами, квазистатический процесс можно себе представить как непрерывно разворачивающуюся во времени цепочку равновесных состояний. Процесс называется обратимым, если при изменении внешних условий в обратном порядке система проходит в обратном порядке те же состояния, что и при прямом процессе. Состояние термодинамического равновесия описывается с помощью ряда внешних и внутренних макроскопических параметров. Для характеристики состояния системы необходимо задать еще и температуру. Разделение параметров на внешние и внутренние осуществляется следующим образом. Часть влияния окружающей среды на изучаемое тело можно аппроксимировать чисто силовым внешним воздействием, рассмотрев нашу подсистему во внешних силовых полях. Внешние параметры нашей подсистемы представляют собой величины, которые определяют эти внешние силовые поля. Внешние параметры есть функции координат идеализированных источников этих внешних силовых полей. Подчеркну, что по самому своему смыслу внешние параметры не зависят от координат и импульсов самой изучаемой системы. Под внутренними параметрами системы понимают средние значения любых функций координат и импульсов самой этой системы. В только, что рассмотренном примере сосуда с газом, объем, надеюсь всем понятно, является внешним параметром. В качестве примера внутреннего параметра можно привести давление газа на стенку сосуда. Давление по самому своему определению есть среднее значение функции координат и импульсов частиц газа. Поэтому давление для нашей системы будет внутренним параметром. В качестве другого примера можно привести тот же газ, помещенный в поле тяжести. В этом случае у нас появляется еще один внешний параметр – сила тяжести. Сила тяжести является внешним параметром, поскольку она зависит от положения внешних источников тяготения и не зависит от микросостояния самого газа. В качестве еще одного примера можно привести опять тот же газ, помещенный в стационарное электрическое поле. Напряженность поля является внешним параметром, поскольку она определяется положением внешних зарядов, вызывающих это поле. Поляризация же газа есть внутренний параметр, поскольку она определяется положением зарядов в непосредственно в молекулах самого газа. Для того, чтобы не было путаницы в дальнейшем, подчеркну, что температуру мы не будем относить ни к внешним, ни к внутренним параметрам. Она у нас будет стоять особняком. Также отмечу, что в термодинамическом равновесии все внутренние параметры системы являются функцией внешних параметров и температуры. Другими словами, макроскопическое состояние системы, находящейся в равновесии со своим окружением, задается внешними параметрами и температурой. Договоримся о следующих обозначениях, которые будем везде в дальнейшем использовать Совокупность координат и импульсов изучаемой нами системы мы будем обозначать При рассмотрении системы, находящейся в равновесии с окружающей средой, мы очень-очень сложную точную функцию Гамильтона замкнутой системы, состоящей из изучаемого тела и окружающей среды, заменяем на приближенную, которую представляем в виде суммы эффективной функции Гамильтона нашей системы и эффективной функции Гамильтона окружающей среды. Т.е. мы пишем, что
Влияние окружающей среды которое можно с достаточной точностью аппроксимировать чисто силовым внешним воздействием на изучаемое тело, мы учитываем в эффективной функций Гамильтона нашей системы Теплообмен между нашей системой и окружающей средой мы учитываем следующим образом. Мы фиксируем функцию Гамильтона Для системы, находящейся в состоянии равновесия, т.е. при заданных конкретных значениях внешних параметров и температуры, независимыми переменными в функции распределения являются координаты и импульсы только этой системы. Информация об окружающей среде входит в функцию распределения нашей системы через параметрическую зависимость от внешних параметров и температуры. Вводя такую функцию распределения, мы на самом деле при определении вероятности различных микроскопических состояний нашей системы учитываем влияние только макроскопического состояния окружающей среды, которое в данном равновесном состоянии фиксировано, и считаем, что эти вероятности никак не зависят от того, каким микросостоянием окружающей среды реализуется заданное ее макроскопическое состояние.
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.016 с.) |

 . (1)
. (1) , (2)
, (2)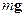 .
. . Всю совокупность импульсов газа обозначим
. Всю совокупность импульсов газа обозначим  . Соответственно, координаты и импульсы термостата обозначим
. Соответственно, координаты и импульсы термостата обозначим  и
и  . Функцию Гамильтона всей замкнутой системы “наш газ+термостат” обозначим
. Функцию Гамильтона всей замкнутой системы “наш газ+термостат” обозначим  . Она, очевидно, зависит как от координат и импульсов нашего газа, так и от координат и импульсов термостата.
. Она, очевидно, зависит как от координат и импульсов нашего газа, так и от координат и импульсов термостата. , состоящей из нашей системы и окружающей среды.
, состоящей из нашей системы и окружающей среды.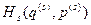 , функцию Гамильтона термостата
, функцию Гамильтона термостата  , и член
, и член  , который описывает неучтенное ранее взаимодействие нашей системы с окружающей средой.
, который описывает неучтенное ранее взаимодействие нашей системы с окружающей средой.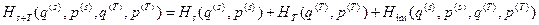 .(3)
.(3) , (4)
, (4)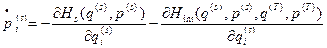 , (5)
, (5) , (6)
, (6) . (7)
. (7)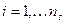 , где
, где  - число степеней свободы нашей системы. Соответственно, индекс пробегает значения
- число степеней свободы нашей системы. Соответственно, индекс пробегает значения  , где
, где  - число степеней свободы термостата.
- число степеней свободы термостата.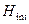 мы не можем систему уравнений для системы
мы не можем систему уравнений для системы  . (8)
. (8)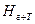 . Она у нас равна Е. Однако при этом мы не фиксируем энергию газа и термостата по отдельности. Энергия газа и энергия термостата могут принимать различные значения, просто эти значения должны быть такими, чтобы их сумма равнялась заданной константе Е. Например, когда энергия газа уменьшается на некоторую величину энергия термостата должна на эту же величину увеличится. Тогда сумма энергий газа и термостата не изменится. Таким образом, несмотря на то, что мы в этой аппроксимации гамильтониана выбросили член, описывающий именно взаимодействие, мы, тем не менее, сохраняем возможность теплообмена между нашей системой и окружающей средой. Выбросив член
. Она у нас равна Е. Однако при этом мы не фиксируем энергию газа и термостата по отдельности. Энергия газа и энергия термостата могут принимать различные значения, просто эти значения должны быть такими, чтобы их сумма равнялась заданной константе Е. Например, когда энергия газа уменьшается на некоторую величину энергия термостата должна на эту же величину увеличится. Тогда сумма энергий газа и термостата не изменится. Таким образом, несмотря на то, что мы в этой аппроксимации гамильтониана выбросили член, описывающий именно взаимодействие, мы, тем не менее, сохраняем возможность теплообмена между нашей системой и окружающей средой. Выбросив член  (9)
(9)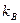 - постоянная Больцмана, Т – термодинамическая температура термостата. С есть нормировочная постоянная.
- постоянная Больцмана, Т – термодинамическая температура термостата. С есть нормировочная постоянная. до
до 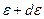 .
. , другая -
, другая -  . При этом мы будем считать две эти поверхности очень-очень близкими, т.е будем считать, что
. При этом мы будем считать две эти поверхности очень-очень близкими, т.е будем считать, что  .
.
 (10)
(10) - объем фазового пространства, ограниченный изоэнергетической поверхностью
- объем фазового пространства, ограниченный изоэнергетической поверхностью 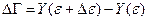 . (11)
. (11) . Малым параметром всегда нужно пользоваться. По малому параметру всегда нужно разлагаться в ряд. Поэтому, естественно, мы должны разложить
. Малым параметром всегда нужно пользоваться. По малому параметру всегда нужно разлагаться в ряд. Поэтому, естественно, мы должны разложить 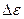 .
.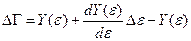 . (12)
. (12) . (13)
. (13) и
и  , дается выражением
, дается выражением . (14)
. (14) есть явная функция энергии газа. Она является неявной функции координат и импульсов нашего газа. Координаты и импульсы входят в эту функцию только в виде определенной комбинации, которая представляет собой функцию Гамильтона нашего газа. Тогда
есть явная функция энергии газа. Она является неявной функции координат и импульсов нашего газа. Координаты и импульсы входят в эту функцию только в виде определенной комбинации, которая представляет собой функцию Гамильтона нашего газа. Тогда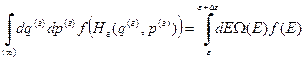 , (15)
, (15) . (16)
. (16) . (17)
. (17) .
. . Другое событие обозначим цифрой 2, его вероятность обозначим
. Другое событие обозначим цифрой 2, его вероятность обозначим 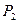 . Тогда вероятность того, что произойдет какое-то из этих событий – или событие 1, или событие 2
. Тогда вероятность того, что произойдет какое-то из этих событий – или событие 1, или событие 2 . (18)
. (18) . Второе событие состоит в том, что наш газ находится в другом элементарном объеме его фазового пространства, окружающем другую точку
. Второе событие состоит в том, что наш газ находится в другом элементарном объеме его фазового пространства, окружающем другую точку  . Поскольку эти события являются несовместными, то согласно теореме сложения вероятностей вероятность того, что наш газ будет находится в каком-то из этих элементарных объемов есть
. Поскольку эти события являются несовместными, то согласно теореме сложения вероятностей вероятность того, что наш газ будет находится в каком-то из этих элементарных объемов есть . (19)
. (19) . (20)
. (20) есть
есть . (21)
. (21)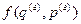 координат и импульсов нашего газа, т.е. равновесное значение соответствующего внутреннего параметра, есть
координат и импульсов нашего газа, т.е. равновесное значение соответствующего внутреннего параметра, есть . (22)
. (22)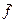 нашего газа есть функция двух независимых переменных: внутреннего параметра – объема газа и температуры термостата.
нашего газа есть функция двух независимых переменных: внутреннего параметра – объема газа и температуры термостата. и
и  . Совокупность координат и импульсов окружающей среды будем обозначать
. Совокупность координат и импульсов окружающей среды будем обозначать  . Один- i-ый - внешний параметр будем обозначать
. Один- i-ый - внешний параметр будем обозначать  (буквой
(буквой  . (23)
. (23) . Когда мы пишем функцию Гамильтона нашей системы, то мы идеализируем окружающую среду, представляя ее в виде совокупности источников классических силовых полей, на которые наша система не оказывает никакого воздействия. Другими словами, при написании гамильтониана нашей системы, мы всю окружающую среду заменяем внешними силовыми полями. Эти внешние силовые поля определяются внешними параметрами. Поэтому эффективная функция Гамильтона нашей системы параметрически зависит от внешних параметров.
. Когда мы пишем функцию Гамильтона нашей системы, то мы идеализируем окружающую среду, представляя ее в виде совокупности источников классических силовых полей, на которые наша система не оказывает никакого воздействия. Другими словами, при написании гамильтониана нашей системы, мы всю окружающую среду заменяем внешними силовыми полями. Эти внешние силовые поля определяются внешними параметрами. Поэтому эффективная функция Гамильтона нашей системы параметрически зависит от внешних параметров.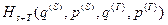 всей замкнутой системы, но при этом мы не фиксируем по отдельности гамильтониан нашей системы
всей замкнутой системы, но при этом мы не фиксируем по отдельности гамильтониан нашей системы  . Этим мы оставляем возможность теплообмена между нашей системой и окружающей средой. В результате мы получаем, что различные значения энергии нашей системы могут реализовываться с различной вероятностью, которая определяется температурой.
. Этим мы оставляем возможность теплообмена между нашей системой и окружающей средой. В результате мы получаем, что различные значения энергии нашей системы могут реализовываться с различной вероятностью, которая определяется температурой.


