
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квантовая теория проводимости металловСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
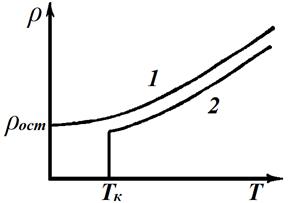
Рассмотрим процесс проводимости с квантовой точки зрения. В предыдущей лекции было сказано, что при объединении атомов в кристаллическую решетку происходит снижение высоты стенок потенциального барьера вокруг ядра каждого атома. При этом внешние (валентные электроны) получают возможность при определенных условиях перемещаться по всему кристаллу, электроны же внутренних оболочек остаются на своих местах. Для металлической решетки условием освобождения электронов является воздействие на кристалл энергии порядка 10–22 эВ, т.е. энергии теплового движения при любой температуре достаточно, чтобы электрон оторвался от ядра и стал свободным. Таким образом, в отличие от полупроводников, металлы всегда имеют электроны проводимости. Поэтому при рассмотрении процесса проводимости изучают не факторы, влияющие на образование свободных электронов, а наоборот – факторы, мешающие проводимости. Напомним, что в направленном движении зарядов в металлах могут участвовать только электроны (понятие дырка здесь не возникает). Отличие механизмов проводимости в металлах и полупроводниках, объясняет обратную (по отношению к случаю полупроводников) зависимость электропроводности от температуры (рис. 12.8). В металлах наблюдается уменьшение проводимости с ростом температуры. Это связано с одним из факторов, определяющих проводимость металла – усилением тепловых колебаний кристаллической решетки, что сопровождается увеличением числа столкновений свободных электронов с положительными ионами решетки – увеличением сопротивления.
Рис. 12.8. Зависимость удельного сопротивления металлов от температуры При понижении температуры число столкновений электронов с атомами решетки снижается и при 0 K обращается в нуль. Сопротивление металла также зависит от того, насколько идеальной является кристаллическая решетка. Реальные кристаллы имеют довольно много разнообразных дефектов. Искажение строго периодичной структуры может быть обусловлено заменой атомов решетки инородными атомами, появлением атомов в междоузлиях, наконец, отсутствием каких-либо атомов решетки (вакансии). Любой из этих дефектов может оказывать влияние на движение электрона в кристалле, причем при небольшой концентрации дефектов от температуры это влияние не зависит. При температуре 0 K, когда колебания решетки отсутствуют, остаточное сопротивление металлов, не переходящих в сверхпроводящее состояние (рис. 12.8 кривая 1), будет обусловлено дефектностью кристаллической решетки. Если в единице объема металла имеется n свободных электронов. Дрейфовой скоростью электронов называют среднюю скорость перемещения электрона в пределах кристалла: В отсутствие внешнего поля дрейфовая скорость равна нулю и электрический ток в металле отсутствует. При наложении на металл внешнего электрического поля напряженностью
где Тогда уравнение, описывающее поведение электронов в металле будет иметь вид: Решив это уравнение, можно найти дрейфовую скорость электронов в металле, находящемся во внешнем электрическом поле:
Тогда плотность тока в металле равна:
где n – количество свободных электронов в данном объеме, другими словами – концентрация электронов в металле. Сравнивая полученное выражение с законом Ома в дифференциальной форме: Сверхпроводимость В области низких температур наблюдается явление сверхпроводимости – резкого падения сопротивления материала. Впервые это явление было обнаружено в 1911 г. Камерлингом-Оннесом для ртути при температуре 4.2 К. Экспериментально сверхпроводимость можно наблюдать двумя способами: 1. Включив в общую цепь звено из сверхпроводника. В момент перехода в сверхпроводящее состояние разность потенциалов на концах сверхпроводящего участка будет равна нулю. 2. Поместив кольцо из сверхпроводника в перпендикулярное к нему магнитное поле. Охладив кольцо ниже температуры перехода в сверхпроводящее состояние, выключают поле. В результате в кольце индуцируется незатухающий электрический ток, циркулирующий бесконечно долго. Такой эксперимент был поставлен: кольцо поддерживали при необходимой температуре и ток в нем без стороннего поля наблюдался в течение двух лет. Далее эксперимент было решено прекратить. Кроме отсутствия электрического сопротивления, для сверхпроводящего состояния вещества характерен так называемый эффект Мейснера: вытеснение магнитного поля из объема проводника. Формально это можно описать равенством нулю магнитной проницаемости вещества μ. Теория сверхпроводимости была разработана в 1957 г. Бардиным, Купером и Шиффером. Проведенные к настоящему моменту экспериментальные исследования подтверждают эту теорию. Суть ее заключается в следующем: в металле, помимо сил кулоновского отталкивания, между электронами возникает особый вид притяжения. При низких температурах это притяжение оказывается сильнее кулоновского отталкивания. В результате свободные электроны объединяются в так называемые куперовские пары. Электроны, входящие в пару имеют противоположно направленные спины. Поэтому спин каждой пары оказывается равным нулю, то есть куперовская пара представляет собой бозон (см. раздел 10). Энергетический спектр таких частиц будет отличаться от спектра электрона в атоме. При этом бозоны склонны существовать в основном энергетическом состоянии E0 и с большим трудом переходить в возбужденное состояние E1, поскольку для этого необходимо приложить достаточно большую энергию. Эта энергия называется энергией связи – она равна энергии, которую нужно затратить для разрушения связи. Таким образом, основное состояние куперовской пары и ее первое возбужденное состояние разделены промежутком, равным энергии связи этой пары. Значения энергии E, попадающие в промежуток от E0 до E1, будут запрещенными для куперовской пары (возникает запрещенная зона). Следовательно, куперовские пары, прядя в согласованное движение, остаются в этом состоянии неограниченно долго. Такое согласованное движение купровских пар и есть ток сверхпроводимости. Достаточно сильное магнитное поле Bk разрушает сверхпроводящее состояние материала. Существует также предельное значение тока Ik, который можно пропустить через сверхпроводник, не разрушив данное состояние. Такой ток достаточен, чтобы перевести куперовскую пару в возбужденное состояние, т.е. разрушить ее. При значениях тока, пропускаемого через сверхпроводник, меньших Ik система не будет возбуждаться, что и будет равносильно протеканию тока без электрического сопротивления. Для сверхпроводящего состояния вещества также наблюдается эффект Джозефсона – если два сверхпроводника разделить тонким слоем диэлектрика (~ 1 нм = 10–9м) или металла в обычном несверхпроводящем состоянии, или тонким слоем полупроводника, то через этот тонкий слой будет течь сверхпроводящий ток. Эту прослойку называют контактом Джозефсона. Электроны преодолевают барьер несверхпроводящего материала благодаря туннельному эффекту. Различают два эффекта Джозефсона – стационарный и нестационарный. Если ток не превышает определенного значения, называемого критическим током контакта, то наблюдается стационарный эффект, при котором падение напряжения на контакте отсутствует. Если ток через контакт превышает критическое значение, то наблюдается нестационарный эффект Джозефсона. В этом случае на контакте возникает разность потенциалов U, и контакт начинает испускать электромагнитное излучение, частота которого равна:
Объясняется это излучение с квантовой точки зрения следующим образом: электронная пара, имеющая заряд 2e, проходя разность потенциалов U, приобретает энергию 2eU. Эта энергия и отдается сверхпроводником в виде излучения с соответствующей частотой. Эффект Джозефсона применяют для измерения малых токов (до 10–10 А), напряжений (до 10–15 В), магнитных полей (до 10–18 Тл) и др. Т.О., эффекты Джозефсона, как же как эффект квантования магнитного потока, подтверждают, что сверх проводимость является чисто квантовым эффектом, проявляющимся в макроскопических масштабах V. ОСНОВЫ ЯДЕРНОЙ ФИЗИКИ
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 724; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.243.29 (0.007 с.) |

 (12.8)
(12.8)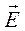 дрейфовая скорость уже не будет равна нулю, согласно закону Ома (см. раздел «электромагнетизм» тему «постоянный ток») дрейфовая скорость электронов конечна и пропорциональна силе
дрейфовая скорость уже не будет равна нулю, согласно закону Ома (см. раздел «электромагнетизм» тему «постоянный ток») дрейфовая скорость электронов конечна и пропорциональна силе  , действующей на электрон, заряд которого равен
, действующей на электрон, заряд которого равен  . Согласно закону Ньютона, силе должно быть пропорционально ускорение, а не скорость. Единственным случаем в механике, когда сила оказывается пропорциональной скорости, является ситуация, когда помимо внешней силы на тело действует еще и сила сопротивления среды. В металле также можно рассмотреть силу сопротивления движению электрона:
. Согласно закону Ньютона, силе должно быть пропорционально ускорение, а не скорость. Единственным случаем в механике, когда сила оказывается пропорциональной скорости, является ситуация, когда помимо внешней силы на тело действует еще и сила сопротивления среды. В металле также можно рассмотреть силу сопротивления движению электрона: (12.9)
(12.9) – коэффициент пропорциональности, в данной ситуации
– коэффициент пропорциональности, в данной ситуации  , m* – эффективная масса электрона (см. раздел 11), τ – представляет собой время релаксации, которое характеризует процесс восстановления равновесия между электронами и кристаллической решеткой, которое было нарушено действием внешнего поля
, m* – эффективная масса электрона (см. раздел 11), τ – представляет собой время релаксации, которое характеризует процесс восстановления равновесия между электронами и кристаллической решеткой, которое было нарушено действием внешнего поля  .
. (12.10)
(12.10) (12.11)
(12.11) (12.12)
(12.12) , получим, что:
, получим, что:  (12.13)
(12.13) (12.14)
(12.14)


