
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитное поле в веществе. Вектор намагниченностиСодержание книги
Поиск на нашем сайте
для количественного описания намагничения магнетиков вводят векторную величину — намагниченность, определяемую магнитным моментом единицы объема магнетика:
где вектор магнитной индукции результирующего магнитного ноля в магнетике равен векторной сумме магнитных индукций внешнего поля В 0 (поля, создаваемого намагничивающим током в вакууме) и поля микротоков В ' (поля, создаваемого молекулярными токами):
где В 0= m 0 Н Ток, текущий по боковой поверхности цилиндра, подобен току в соленоиде и создает внутри него поле, магнитную индукцию В' которого можно вычислить, учитывая формулу (119.2) для N = 1 (соленоид из одного витка):
где I' — сила молекулярного тока, l — длина рассматриваемого цилиндра, а магнитная проницаемость m принята равной единице. С другой стороны, I'/l — ток, приходящийся на единицу длины цилиндра, или его линейная плотность, поэтому магнитный момент этого тока p = I'lS/l = I'V/l, где V — объем магнетика. Если Р — магнитный момент магнетика объемом V, то намагниченность магнетика
Сопоставляя (133.2) и (133.3), получим, что
или в векторной форме
Подставив выражения для В 0 и В' в (133.1), получим
или
Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора В) является обобщением закона (118.1):
где I и I' — соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым контуром L. Таким образом, циркуляция вектора магнитной индукции В по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. Вектор В, таким образом, характеризует результирующее поле, созданное как макроскопическими токами в проводниках (токами проводимости), так и микроскопическими токами в магнетиках, поэтому линии вектора магнитной индукции В не имеют источников и являются замкнутыми. Из теории известно, что циркуляция намагниченности J по произвольному замкнутому контуру L равна алгебраической сумме молекулярных токов, охватываемых этим контуром:
Тогда закон полного тока для магнитного поля в веществе можно записать также в виде
где I, подчеркнем это еще раз, есть алгебраическая сумма токов проводимости. Выражение, стоящее в скобках в (133.9), согласно (133.5), есть не что иное, как введенный ранее вектор H напряженности магнитного поля. Итак, циркуляция вектора Н по произвольному замкнутому контуру L равна алгебраической сумме токов проводимости, охватываемых этим контуром:
Выражение (133.10) представляет собой теорему о циркуляции вектора Н.
|
|||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 278; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.238.6 (0.006 с.) |


 — магнитный момент магнетика, представляющий собой векторную сумму магнитных моментов отдельных молекул
— магнитный момент магнетика, представляющий собой векторную сумму магнитных моментов отдельных молекул (133.1)
(133.1) (133.2)
(133.2) (133.3)
(133.3)

 (133.4)
(133.4)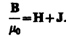


 (133.9)
(133.9) (133.10)
(133.10)


