
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа при перемещении витка с током в постоянном магнитном поле.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим сначала частный случай. Пусть параллельные проводники
где
а для конечной работы
Таким образом, работа, совершаемая магнитным полем над током, равна приращению магнитного потока, умноженного на ток. При выводе предполагалось, что ток Результат справедлив и при произвольном направлении магнитного поля. Чтобы убедится в этом, разложим вектор Докажем теперь, что полученные формулы справедливы для любого витка с током при произвольном перемещении его в постоянном неоднородном магнитном поле. Виток может не только перемещаться, но и произвольно деформироваться. Для доказательства достаточно мысленно разбить виток на бесконечно малые элементы тока и рассмотреть бесконечно малые перемещения их. При бесконечно малом перемещении элемента тока магнитное поле, в котором он перемещается, может считаться однородным. Суммируя перемещения всех малых элементов, получаем выражение для элементарной работы. Интегрируя затем, получаем вновь выражение для конечной работы. Необходимо подчеркнуть, что ток в витке должен поддерживаться постоянным. Если в магнитном поле перемещается катушка с намотанным на нее многократно проводом, то в работе по ее перемещению необходимо учесть перемещение каждого витка. И тогда в окончательном выражении работы будет вместо магнитного потока стоять сумма магнитных потоков через все витки
Величина
где
Самоиндукция. Коэффициенты индуктивности. Мы знаем, что всякий ток в проводнике создает магнитное поле. Но это поле, начав изменяться, в свою очередь влияет на вызвавший его ток. Это явление называется самоиндукцией.
Если в пространстве нет ферромагнетиков, то магнитный поток через виток с током пропорционален протекающему в нем току
.
Для длинного соленоида
В системе СИ единицей измерения коэффициента самоиндукции является Гн (генри, Если рядом расположенных проводников с токами много, то кроме коэффициентов самоиндукции вводятся коэффициенты взаимной индукции, которые описывают часть ЭДС индукции, возникающей под воздействием другого тока
Коэффициенты взаимной индукции также измеряются в Гн.
Энергия магнитного поля. Вычисление энергии проводника приводит к формуле
В случае длинного соленоида эта формула преобразуется к
Отсюда легко получить плотность энергии магнитного поля (
Эта формула годится при любой конфигурации магнитного поля.
Ток смещения. Начнем с теоремы о циркуляции магнитного поля:
где
Теперь применим оператор дивергенции к уравнению (1). Так как всегда дивергенция, примененная к ротору, дает нуль, то получается:
Такой вариант закона сохранения заряда получается только в случае, когда плотность заряда Такой член можно получить, воспользовавшись теоремой Гаусса для вектора смещения электрического поля:
Эта формула получена из известной вам теоремы Гаусса умножением на
Дифференцируя это соотношение по времени, получаем:
Точка над вектором смещения означает производную по времени. Пользуясь теперь уравнением закона сохранения заряда, получаем:
то есть производная по времени от вектора смещения должна быть добавлена в теорему циркуляции магнитного поля. Максвелл назвал этот член плотностью тока смещения Окончательно
Уравнение (2) является одним из уравнением Максвелла. Вопрос: а действительно ли существует такой ток смещения. Ответ: результат Максвелла давно подтвержден на эксперименте. На рисунке справа представлен один из таких экспериментов. На нем нарисован конденсатор, присоединенный к цепи переменного тока. В случае переменного тока в промежутке между обкладками электрическое поле становится переменным и там же возникает магнитное поле, которого в электростатике не наблюдается. То есть Максвелл (теоретик) открыл, что изменение электрического поля создает магнитное поле. Аналогично закону электромагнитной индукции.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 687; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.92.5 (0.006 с.) |


 и
и 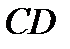 (см. рис.) помещены в однородное постоянное магнитное поле, перпендикулярное к плоскости рисунка и направленное к нам. Слева находится источник тока, не показанный на рисунке. По проводам может свободно перемещаться проводящий мостик
(см. рис.) помещены в однородное постоянное магнитное поле, перпендикулярное к плоскости рисунка и направленное к нам. Слева находится источник тока, не показанный на рисунке. По проводам может свободно перемещаться проводящий мостик 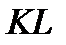 , замыкающий ток
, замыкающий ток  , текущий по проводам левее мостика. Если
, текущий по проводам левее мостика. Если  — длина мостика, то на него магнитное поле действует с силой
— длина мостика, то на него магнитное поле действует с силой  . При перемещении мостика на
. При перемещении мостика на  эта сила совершает работу
эта сила совершает работу ,
, — площадь прямоугольника
— площадь прямоугольника  . Величина
. Величина  есть магнитный поток через тот же прямоугольник. Обозначив его через
есть магнитный поток через тот же прямоугольник. Обозначив его через  , получим для элементарной работы
, получим для элементарной работы ,
, .
. при перемещении мостика
при перемещении мостика 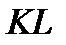 поддерживается постоянным.
поддерживается постоянным. на три составляющие:
на три составляющие:  . Составляющая вдоль мостика
. Составляющая вдоль мостика  параллельна току в нем и не оказывает на мостик силового воздействия. Составляющая
параллельна току в нем и не оказывает на мостик силового воздействия. Составляющая  вдоль перемещения дает силу, перпендикулярную к перемещению и работы не производит. Работа производится лишь составляющей
вдоль перемещения дает силу, перпендикулярную к перемещению и работы не производит. Работа производится лишь составляющей  , перпендикулярной к плоскости рисунка, в которой перемещается мостик
, перпендикулярной к плоскости рисунка, в которой перемещается мостик  .
. .
. носит название потокосцепления. Если все потоки одинаковы, то
носит название потокосцепления. Если все потоки одинаковы, то ,
, — число витков катушки, а работа по перемещению катушки суть
— число витков катушки, а работа по перемещению катушки суть .
. носит название коэффициента самоиндукции провода. Он зависит только размеров и конфигурации проводника. Тогда закон электромагнитной индукции будет следующим
носит название коэффициента самоиндукции провода. Он зависит только размеров и конфигурации проводника. Тогда закон электромагнитной индукции будет следующим

 .
. вычисляется и равно
вычисляется и равно , где
, где  — плотность витков на единицу длины, а
— плотность витков на единицу длины, а  — объем пространства внутри соленоида.
— объем пространства внутри соленоида. ).
).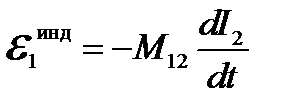 .
. .
. .
. )
) .
. .
. означает алгебраическую сумму всех токов, пронизывающих поверхность, ограниченную контуром
означает алгебраическую сумму всех токов, пронизывающих поверхность, ограниченную контуром  . Это уравнение может быть переписано в дифференциальном виде:
. Это уравнение может быть переписано в дифференциальном виде: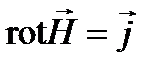 ,
,
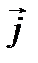 — вектор плотности тока. Как мы сейчас увидим, это уравнение не полно. Вспомним, что закон сохранения электрического заряда в дифференциальной форме выглядит так:
— вектор плотности тока. Как мы сейчас увидим, это уравнение не полно. Вспомним, что закон сохранения электрического заряда в дифференциальной форме выглядит так: .
. .
. не зависит от времени, т.е. задача стационарна. Но уравнения электромагнитного поля должны выполняться и для переменных полей. Следовательно, к правой части уравнения (1) надо добавить член, чтобы дивергенция от правой части всегда обращалась в нуль.
не зависит от времени, т.е. задача стационарна. Но уравнения электромагнитного поля должны выполняться и для переменных полей. Следовательно, к правой части уравнения (1) надо добавить член, чтобы дивергенция от правой части всегда обращалась в нуль. .
. (
( в вакууме), заменой вектора напряженности электрического поля на вектор смещения и обозначением алгебраической суммы всех зарядов внутри объема, ограниченного замкнутой поверхностью
в вакууме), заменой вектора напряженности электрического поля на вектор смещения и обозначением алгебраической суммы всех зарядов внутри объема, ограниченного замкнутой поверхностью  , через
, через  . В дифференциальном виде это уравнение выглядит так:
. В дифференциальном виде это уравнение выглядит так: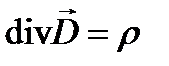 .
. .
.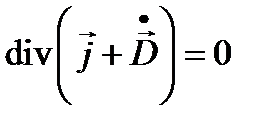 ,
,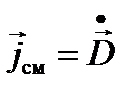 , а сумму обычного тока и тока смещения полным током. Конечно ток смещения никакой не ток, но ведет себя подобно ему в нестационарных задачах.
, а сумму обычного тока и тока смещения полным током. Конечно ток смещения никакой не ток, но ведет себя подобно ему в нестационарных задачах. .
.




