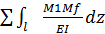Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о взаимности работ и взаимности перемещенийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть балка имеет два состояния: 1)
2)
Где ∆12 – перемещение в точке 1 от действия силы, приложенной в точке 2. ∆21 – перемещение в точке 2 от силы, приложенной в точке 1. Для вывода теоремы сначала балку загружаем силой F1, а затем силой F2
Совершенная работа равна: W=W11+W22+W12=
W=W22+W11+W21= Т.к. силы одинаковы, то и работа одинакова, из этого следует: F1∙∆12 = F2∙∆21 – теорема о взаимности работ (теорема Бетти): Работа сил первого состояния на перемещение второго состояния равна работе сил второго состояния на перемещение первого состояния. Если принять F1=F2=1 (безразмерная величина), то получим теорему о взаимности перемещений (теорема Максвелла): δ12=δ21- перемещение от единичной силы. Th: перемещение в точке приложения первой единичной силы по её направлению, вызванной второй единичной силой равно перемещению в точке приложения второй единичной силы по её направлению, вызванной первой единичной силой.
10.Графоаналитеческий способ решения интеграла Мора (способ Верещагина) Если загружен. сис-мы имеют ряд участков с различными изгиб. моментами, то вычисления интеграла несколько затруднительно. Поэтому применяют способ Верещагина. Пусть груз. эпюра моментов имеет криволинейное очертание, а единич. эпюра изгиб. моментов имеет линейное(рисунок).В этом случае интеграл Мора
Статический момент любой фигуры равен произведению площади на расстояние от оси до центра тяжести фигуры где w- площадь грузовой эпюры МF; Zc- растояние до центра тяжести.
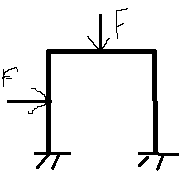
Статически неопределимые системы.Метод расчета. Основная и эквивалентная система. Статически неопределимыми балками(рамами) наз. балки(рамы) у которых все неизвестные реакции опор невозможно определить используя только уравнения статики, тк они имеют линии связи(реакции). Степень статич неопред-ти опред-ся разностью между числами неизвестных реакций и уравнений статики.
Балки имеют 4 опорные связи,т.е 4 опорные р-ции. А ур-й статики для плоской сист. Можно составить 3, следовательно балка явл. 1 раз статич. Неопределимой. Для раскрытия статической неопред-ти необход. к ур-ю статики составить доп. Ур-е исходя из перемещения сист. Их кол-во опред. степень статич неопределимости. Если линейных неизвестных несколько то доп. ур-я сост-ся исходя из деформационных условий(прогибов) на опору балки используя метод начальных параметров. Сост. Ур-я статики и доп. Ур-я для заданной балки: Z=0; Y=0; M(B)=0. Доп. Ур-е запишем из условия, что прогиб на опоре B=0. EIY(B)=0. У некоторых сист. степень статич. неопред. высокая(неразрезные балки). Доп. ур-е составляеться исходя из деформационных условий(углов поворота сечения) на промежуточных опорах балкииспользуя метод сил. Из совместного решения ур-й статики и доп-х ур-й находим все неизвестные реакции Установив степень статической неопределимости составляеться основная система. Под основной системой понимаеться такая статически определимая система, которая получается из статически неопределимой путем отбрасывания линейных связей.
Связей 6, уравнений статики 3. 6-3=3 - 3 раза статич неопред сист Рисунок. Основных систем можно выбрать множество. При выборе основной системы необходимо что бы она была геометрически и мгновенно неизменяемой. Рисунок. «геометрич измененная», «мгновенно измененная» К мгновенно измененным сист относиться системы у которых реакции опор пересекаются в одной точке. Если к основной сист. приложить отброшенные связи и нагрузку, то получим эквивалентную систему. рассмотрим 1-ю осн ситему. Рисунок рассмотрим 2-ю основную систему. Рисунок
Основы метода сил. расчет по методу сил осуществляеться в след. порядке: 1) Устанавливаем степень статической неопределимости 2) Выбираем основную и эквивалентную системы. отбрасывая линии связи и заменяя их неизвестными силами Х1,Х2,Х3. 3) Записывают условия эквивалентности заданой и эквиваленнтной систем по перемещению заданая система Если у заданной сист перемещение по направлению неизвестных сил Х1,х2,Х3 отсутствует.то условия эквивалентности будут иметь вид: Выразим эти перемещения от каждой неизвестной силы и от внешней нагрузки
Что касается неизвестных Х1,Х2,Х3, то их влияние на перемещение можно представить ввиде:
Получ. ур-я наз. каноническими ур-ми метода сил. Коэффициенты Перемещение 1) Опред. методом Мора-Верещагина
В соответствии с теорией о взаимности перемещений: 2) После определения коэффициентов и грузовыхчленов канонических ур-ий при совместном их решении находят значения усилий в связях х1,х2,х3. 3) Используя уравнения статики находят все неизвестные реакции опор.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1251; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.83.149 (0.007 с.) |




 +
+  + F1∙∆12
+ F1∙∆12
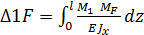 .(ВЫВОД)
.(ВЫВОД) ;
;  dw =Sy- статический момент площади груз. Эпюры моментов относительно оси У.
dw =Sy- статический момент площади груз. Эпюры моментов относительно оси У.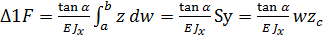 ;
;  Однако имея значение момента от единичной нагрузки под центром тяжести груз. Эпюры
Однако имея значение момента от единичной нагрузки под центром тяжести груз. Эпюры 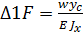 .Поскольку к балке может быть приложена несколько нагрузок, то перемещение определяют для каждого участка балки
.Поскольку к балке может быть приложена несколько нагрузок, то перемещение определяют для каждого участка балки 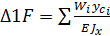 – формула Верещагина, т.е перемещение равно площади криволинейной эпюры на ординату прямолинейной расположенной под центром тяжести криволинейной эпюры. В практических расчётах площадь груз. эпюры разбивают на простейшие эпюры (рисунки).
– формула Верещагина, т.е перемещение равно площади криволинейной эпюры на ординату прямолинейной расположенной под центром тяжести криволинейной эпюры. В практических расчётах площадь груз. эпюры разбивают на простейшие эпюры (рисунки).



 эквив.сист
эквив.сист =0,
=0,  ,
,  =0.
=0. =
=  ,
, =
=  ,
,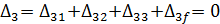 . Перемещения:
. Перемещения: =
=  Х1;
Х1;  =
=  Х2;
Х2;  =
=  Х3 т.е определение перемещений
Х3 т.е определение перемещений 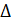 от единич. сил приложенных в направл. связей умножают их на соответствующие неизвестные силы X. после этого ур-е перемещений по направлению 3-х неизвестных связей примут вид:
от единич. сил приложенных в направл. связей умножают их на соответствующие неизвестные силы X. после этого ур-е перемещений по направлению 3-х неизвестных связей примут вид: =0
=0 =0
=0 =0
=0 и др. явл. единичными перемещениями,тк вызваны единичными силами.
и др. явл. единичными перемещениями,тк вызваны единичными силами. явл. грузовыми перемещениями,тк вызваны задаными нагрузками и наз. связаными ими грузовыми членами.
явл. грузовыми перемещениями,тк вызваны задаными нагрузками и наз. связаными ими грузовыми членами.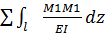 ,
, 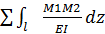 ,
,  =
=