
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамические нагрузки. Определение. Учет сил инерцииСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
При статическом действии нагрузка изменяется медленно, до своего конечного значения. Определим динамическое усилие на каком-то расстоянии z. Динамическое напряжение больше статических. ПРИМЕР: Подъемный механизм весом Q=4,5 кН поднимает груз весом G=8 кН Jx=1326 см4 Jo=5,87 см4
Удар. Определение. Основные допущения принятые в теории удара. Ударное действие нагрузок происходит, когда скорость нагрузки изменяется быстро. Происходит это в частности при соприкосновении движущегося тела с неподвижным. Определить инерционные силы методом механики невозможно, поэтому используют закон сохранения энергии. В основу удара положены следующие допущения: 1) деформация происходит в упругой стадии. 2) удар является неупругим, т.е. тело после удара не отделяются друг от друга. 3) кинетическая энергия падающего груза полностью переходит в потенциальную энергию деформируемого тела(потери части энергии в теплоту и колебательное движение принебрегаем): T=U (кинет.эн=потенц.эн). 4) массой неподвижного тела принебрегаем, т.е. считаем, что оно мало по сравнению с массой ударяющего тела.
Определение динамического коэфф. при ударе. Предположим имеем невесомую сис-му на которус с высоты h падает груз F. Под действ. падающего груза произойдет динамическая деформация:
Кинетическая энергия падающего груза= работе совершенной этим грузом:
∆ст=(F*l)/(E*A)=F/(E*A/l)=F/c c=E*A/l U=(F/2)*(F/c)*(c/c)=(∆ст*с)/2 с – коэффиц. жесткости Коэф-нт жесткости «с» величина постоянная, зависит от упругих св-в материала и размеров. Покажем коэф-нт жесткости при изгибе: ∆ст=(F* ∆ст=F/(3*E*I/ C=3*E*I/
∆cт=(F* C=48*E*I/ Т.о. величина с всегда известна Приударных нагрузках деформации происходят такие же как и при статическом нагружении, но быстрее:
c=F/∆ст => приравняем кинетическую и потенциальную энергию при ударе: F(h+∆д)= 2∆cт*h+2∆cт*∆д=
Получим квадратное ур-е, его решение имеет вид:
Динамический коэфф. можно представить в др виде, зная связь между скоростью и высотой падения:
Можно выразить его через энергию:
Продолный удар. РИСУНОК.
Поперечный удар На балку падает груз F с высоты h (РИСУНОК)
Предположим что груз падает по середине пролётной балки
37. Испытание материалов на удар (ударная проба). Механические характеристики материалов устанавливаются при медленном погружении, с увеличением скорости нагружения увеличиваются предел прочности и предел текучести.
Для оценки пригодности материала к динамическим нагрузкам производится ударная проба материала. Испытание проводится на механическом копре.
В результате опыта определяется не напряжение, а работа затраченная на разрушение и определяется ударная вязкость. ak
где А – работа. Чем больше ударная вязкость, тем лучше материал сопротивляется ударным нагрузкам.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.65.133 (0.007 с.) |



 )=0
)=0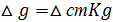 - динамическое перемещение
- динамическое перемещение



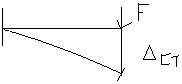
 )/3*E*I, (из справочника)
)/3*E*I, (из справочника) 2
2 =
=  *с/2
*с/2 *F/2∆cт
*F/2∆cт
 =1+
=1+  – динамический коэфф. без учета массы сис-мы
– динамический коэфф. без учета массы сис-мы

 ;
;  ;
; 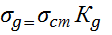 ;
; 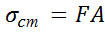 .Воспользуемся приближ. значением
.Воспользуемся приближ. значением 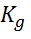 .
. 
 ,где V=Al- объём тела. Из выражения следует, что чем больше модуль Юнга и меньше объем тела, тем больше динамич. напряжение. Динамич. коэф-ент если неподвижное тело имеет выточки(рисунок).
,где V=Al- объём тела. Из выражения следует, что чем больше модуль Юнга и меньше объем тела, тем больше динамич. напряжение. Динамич. коэф-ент если неподвижное тело имеет выточки(рисунок). 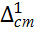 =
=  ;
; 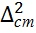 =
=  -
-  . Предположим,что длина
. Предположим,что длина 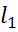 очень мала, то приближенно можно записать
очень мала, то приближенно можно записать  =
= 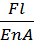 . Предположим что стержни равнопрочны
. Предположим что стержни равнопрочны  , то динамич. коэф-ты равны
, то динамич. коэф-ты равны 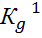 =
= 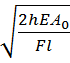 ;
; 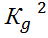 =
=  ↔
↔  . Поэтому
. Поэтому динамич. напряжение во втором стержне больше.
динамич. напряжение во втором стержне больше. ;Ммах =
;Ммах =  (из справочника)
(из справочника) ;
;  ;
; 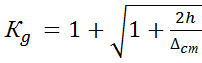 , где
, где  гиб в точке падения груза от его статического действия.
гиб в точке падения груза от его статического действия.  ;
;  ;
;  ;
;  ;
;  )=
)=  ,где i- радиус инерции,
,где i- радиус инерции,  расстояние от нейтральной линии до наибольшей удалённой точки. Динамическое напряжение при поперечном ударе можно уменьшить путём установки податливой опоры пружины(РИСУНОК)
расстояние от нейтральной линии до наибольшей удалённой точки. Динамическое напряжение при поперечном ударе можно уменьшить путём установки податливой опоры пружины(РИСУНОК)  увеличивается,
увеличивается,  -уменьшается↔уменьшается динамич. напряжение.
-уменьшается↔уменьшается динамич. напряжение. (Дж/м2),
(Дж/м2),


