
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент инерции ненагруженного столаСодержание книги
Поиск на нашем сайте
Определите момент инерции ненагруженного стола методом «эталонного» тела. Используйте малые цилиндры. Радиус цилиндров R 0 = 24.0 мм масса m = m 1+ m 2= 1011 г. Определите сначала период колебаний стола, не нагружая его (угол отклонения выбираем в пределах 20-30 градусов): T 0 = мс. Установите два цилиндра симметрично на расстоянии r = 100 мм от оси стола. Период колебаний стола с грузами: Т = мс. П р и м е ч а н и е. При проведении расчетов массы цилиндров и всех ниже предложенных тел удобно брать в граммах, но все остальные величины следует переводить в единицы системы СИ, т.е. миллисекунды в секунды, миллиметры в метры и т.д. Тогда получаемые значения моментов инерции будут получаться в г·м 2, что намного удобнее, ввиду того, что моменты инерции всех тел в настоящей работе достаточно малы. Момент инерции цилиндров («эталон») I 1 = (m 1 +m 2)·(r 2 + R 02/2) = г м2. Из соотношений: I = Т 2 kпарR 2/(4p2); I 0 = Т 02 kпарR 2/(4p2); I = I 0 + I 1; Находим момент инерции I стола вместе с грузами I = I 1 T 2/(T 2 - Момент инерции ненагруженного стола, I 0 = I 1 T 02/(T 2 - Значение жесткости пружин (при вычислении перевести I 1 в кг м2) kпар = 4p2 I 1/(R 2(T 2 – T 02)) = Н/м. ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ РАЗЛИЧНЫХ ТЕЛ Положите одно из предложенных тел на центр поворотного стола масса тела m = г, характерный размер (длина, радиус) R = мм (или l = мм). Значения масс тел указаны на них, характерные размеры измеряются линейкой. Измерить момент инерции всех предложенных тел (стержень, полушар, диск, кольцо) и сделать вывод по полученным результатам. 1) Стержень: масса стержня m = г, характерный размер (длина) l = мм. Период колебаний стола со стержнем: Т = мс. Момент инерции стержня:
Расчетное значение момента инерции:
2) Полушар: масса полушара m = г, характерный размер (радиус) R = мм. Период колебаний стола с полушаром: Т = мс. Момент инерции полушара:
Расчетное значение момента инерции:
3) Диск: масса диска m = г, характерный размер (радиус) R = мм. Период колебаний стола с диском: Т = мс. Момент инерции диска:
Расчетное значение момента инерции:
4) Кольцо: масса кольца m = г, радиусы Rвнутр =, Rвнешн = мм, Rср = мм. Период колебаний стола с кольцом: Т = мс. Момент инерции кольца:
Расчетное значение момента инерции:
ТЕОРЕМА ШТЕЙНЕРА Любое из тел может быть расположено на различных расстояниях от оси вращения стола (фиксация расстояний с шагом 20 мм). Для проверки теоремы Штейнера измерить моменты инерции стола с двумя цилиндрами массой m = 1011 г на различных расстояниях от оси вращения стола. Результаты записать в предложенную таблицу. Таблица 6.1
r 1 = 4 см; r 2 = 6 см; r 3 = 8 см; r 4 = 10 см. ИЗМЕРЕНИЕ МОМЕНТА ИНЕРЦИИ С ПОМОЩЬЮ ПРУЖИН ИЗВЕСТНОЙ ЖЕСТКОСТИ (эксперименты на шкиве стойки стола) Для получения колебательной системы через шкив радиуса R стойки перекидывается длинная нить, концы которой посредством двух пружин прикрепляются к зацепам на основании стойки. kпар = Н/м. Момент инерции не нагруженного шкива Период колебаний шкива Тшк = мс при R = мм; Момент инерции шкива Iшк = kпарR 2 Момент инерции стержня L =мм, m = г Период колебаний шкива со стержнем Т = мс. Момент инерции шкива со стержнем I = kпарR 2 Т 2/(4p2) = г м2. Момент инерции стержня: Расчётное значение: Iст = mL 2/12 = г м2. По результатам измерений Icт = I – Iшк = г м2. Сделать сравнительный анализ с методом п. 2. ЛАБОРАТОРНАЯ РАБОТА № 7 Цель работы: познакомиться с одним из методов определения Ср / Сv. Приборы и принадлежности: установка ЛКТ-5, шланг с грушей-помпой, переходной шланг, мембранный манометр, емкость с водой. Краткие теоретические сведения Состояние газа характеризуется тремя величинами – параметрами состояния: давлением Р, объемом V, и температурой Т. Уравнение связывающее эти величины, называется уравнением состояния газа. Для идеального газа уравнением состояния является уравнение Менделеева – Клапейрона:
где m – масса газа, m - масса одного моля, R – универсальная газовая постоянная. Для одного моля:
Теплоёмкостью тела называется количество теплоты, которое нужно сообщить телу, чтобы изменить его температуру на один градус:
Здесь dТ – изменение температуры тела при сообщении ему количества теплоты dQ. Теплоёмкость единицы массы тела называется удельной теплоёмкостью:
Теплоёмкость одного моля вещества называется молярной теплоёмкостью:
Величина теплоёмкости газа зависит от условий его нагревания, т.е. от того, нагревается ли газ при постоянном объёме (обозначим молярную теплоёмкость в этом случае через Сv) или процесс нагревания происходит при постоянном давлении (Ср). Сv и Ср связаны между собой. Эту связь можно получить, пользуясь уравнением состояния (7.2), написанным для одного моля газа, и первым началом термодинамики, которое можно сформулировать следующим образом: количество теплоты dQ, переданное системе, затрачивается на увеличение её внутренней энергии dU и на работу dA, совершаемую системой над внешними телами: dQ = dU + dA. (7.4) Элементарная работа dA = P dV. (7.5) Исходя из определения молярной теплоёмкости (7.3):
При изохорическом процессе V = const, следовательно, dV = 0 и dA = 0 (см. формулу (7.5)), и поэтому Сv = При изобарическом процессе Р = const, следовательно,
Из уравнения состояния газа (7.2) получаем Р dV + V dP = R dT. Но dP = 0 (т.к. Р = const), а поэтому P dV = R dT. Учитывая это равенство и заменяя dU через Сv dT, из выражения (7.7) получим Ср = Сv + R. Таким образом Ср > Cv: при нагревании при постоянном давлении тепло, сообщённое газу, идёт не только на изменение его внутренней энергии, но и на совершение газом работы. Важную роль в термодинамике играет величина g = Ср / Сv, в частности, gвходит в уравнение Пуассона, описывающее адиабатический процесс, т.е. процесс, протекающий без теплообмена с окружающей средой (dQ = 0). Уравнение Пуассона в переменных (Р, V) имеет вид: РV g = const. Из первого начала термодинамики (7.4) для адиабатического процесса следует: dU + dA = 0, откуда dA = - dU = - Cv dT, т.е. работа в этом случае совершается за счёт изменения запаса внутренней энергии газа. Описание метода определения Ср / Сv Создадим в баллоне давление воздуха р 1, превышающее атмосферное давление р 0, затем на короткое время откроем кран в атмосферу. Давление в баллоне упадёт до атмосферного, а оставшийся в баллоне воздух вследствие адиабатического расширения охладится от начальной температуры Т 1 (комнатная) до температуры Т 0, определяемой уравнением адиабаты: р 11-g Т 1g = р 01-g Т 0g. (7.8) После закрытия крана температура воздуха в баллоне постепенно вернётся к комнатной, и давление возрастёт до значения р 2
Из этих соотношений находим g = Ср / Сv:
Если избыточное давление D р 1 = р 1 – р 0 значительно меньше атмосферного давления р 0, то приблизительно
Порядок выполнения работы 1. К штуцеру Ш1 подключите шланг груши – помпы. 2. Соедините баллон (штуцер Ш3) с мембранным манометром для создания высоких давлений. 3. Закройте краны К2 и К3. 4. Откройте кран К1 и накачайте воздух до избыточного давления D р 1 = 200 мм Нg (мм рт. ст.), после чего закройте кран К1. 5. Подождите 1 – 2 минуты, пока установится температура воздуха в баллоне и давление перестанет изменяться. 6. Включите часы в режим «секундомер» кнопкой «mode». 7. На короткое время t = 0…5 с откройте кран К3 баллона и закройте его. Время открытого состояния крана автоматически измерит таймер. П р и м е ч а н и е. Необходимо получить 8 различных значений моментов времени в указанном интервале, для построения графиков (см. пп. 9, 11 и табл. 7.1 и 7.2). Примерные значения времени открытия крана (для построения «удачного» графика) лучше всего стремиться получить близкими к: t 1 ~ 0,50; t 2 ~ 1,00; t 3 ~ 1,50; t 4 ~ 2,00; t 5 ~ 2,50; t 6 ~ 3,00; t 7 ~ 3,50; t 8 ~ 4,00 сек., т.е. отстоящими друг от друга на несколько десятых долей секунды. 8. Подождите 1 – 2 минуты до установления температуры и давления в баллоне. Запишите установившееся избыточное давление D р 2 в таблицу 7.1. 9. Для фиксированного давления D р 1 повторите опыт с различными значениями t (см. примечание к п. 7), заполняя таблицу 7.1. 10. Подключите к штуцеру Ш3 вместо мембранного манометра водяной (штуцер М ), для создания низких давлений, при помощи переходного шланга и повторите пункты 3 – 9, заполняя таблицу 7.2. 11. Постройте графики зависимости ln (D р 2) = F (t) для обоих случаев. Эти графики покажут, какие значения t слишком малы (воздух не успевает выйти из баллона), а какие слишком велики (воздух успевает частично подогреться, пока кран ещё открыт). Экстраполируя графики из области больших t к значению t = 0, найдите «идеальные» значения избыточного давления D р 2 и р 2, нужные для расчёта показателя адиабаты g. Указание. Графики следует строить на одной координатной сетке. Рекомендуемый масштаб по оси «t»: 1 сек в 2-х см, по оси «ln(D p 2)»: 0,1 ед. в 1-м см. 12. Результаты представить в виде: Контрольные результаты Высокие давления: D р 1 = 200 мм.рт.ст = 27,2 кПа, р 1 = р 0 + D р 1 = кПа. Таблица 7.1
Экстраполяция: D р 2 =мм.рт.ст = кПа. По формуле (7.10): g =.
Низкие давления: D р 1 = 200 мм.вод.ст.) = 2,00 кПа. Таблица 7.2
Экстраполяция: D р 2 =мм.вод.ст. = кПа. По формуле (7.11): g =.
13. Сделайте вывод по полученным значениям постоянной адиабаты. 14. Ответьте на следующие контрольные вопросы: 1 Что называется теплоёмкостью тела, удельной теплоёмкостью вещества, молярной теплоёмкостью вещества? В каких единицах измеряются эти величины? 2 Что такое молярная теплоёмкость при постоянном объёме (СV), при постоянном давлении (Ср)? 3 Какова связь между СV и Ср? 4 В чём состоит первое начало термодинамики? 5 Какой процесс называется изохорическим? 6 Какой процесс называется изобарическим? 7 Какой процесс называется адиабатическим? 8 Запишите уравнение Пуассона в переменных P и V, P и Т. 9 Опишите устройство прибора и процессы, происходящие с газом в ходе выполнения работы? ЛАБОРАТОРНАЯ РАБОТА № 8 Цель работы: измерить коэффициент динамической вязкости воздуха. Приборы и принадлежности: ЛКТ-9: электрочайник, соединительные шланги, груша-помпа с зажимом, капилляр; термометр, баллон с двумя штуцерами.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.111.109 (0.007 с.) |

 2) = г м2,
2) = г м2, = г м2.
= г м2.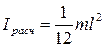 = г м2.
= г м2. = г м2.
= г м2. = г м2.
= г м2. = г м2, или более точно
= г м2, или более точно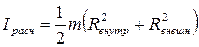 = г м2.
= г м2. ;
;  ; j = 1,2,3.
; j = 1,2,3. /(4p2) = г м2.
/(4p2) = г м2.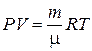 , (7.1)
, (7.1) . (7.2)
. (7.2) (Дж/К).
(Дж/К). (Дж/кг К).
(Дж/кг К). (Дж/моль К). (7.3)
(Дж/моль К). (7.3) .
. . (7.6)
. (7.6) . (7.7)
. (7.7) . (7.9)
. (7.9) . (7.10)
. (7.10) . (7.11)
. (7.11)


